HDU6470 Count-蒲公英云

HDU6470 Count

向右看齐 2021-09-18 12:36 363阅读 0赞

好久没写矩阵快速幂（其实这题可以直接用杜教的BM板子，比赛时突然想练一下矩阵快速幂）
比较难搞的是 n 3 n^3 n3
考虑 n 3 − > ( n + 1 ) 3 n^3 -> (n+1)^3 n3−>(n+1)3,多了 3 n 2 , 3 n , 1 3n^2,3n,1 3n2,3n,1
然后就可以构造一个6x6的矩阵 [ f ( n − 1 ) , f ( n − 2 ) , n 3 , 3 n 2 , 3 n , 1 ] [f(n-1),f(n-2),n^3,3n^2,3n,1] [f(n−1),f(n−2),n3,3n2,3n,1]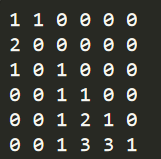
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=123456789;
ll powmod(ll a,ll b) { ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){ if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
ll gcd(ll a,ll b) {  return b?gcd(b,a%b):a;}
const int maxn = 6;
int T;
ll n;
struct Matrix{ 
    ll a[maxn][maxn];
    void init(){     
        memset(a, 0, sizeof(a));
        for(int i=0;i<maxn;++i){ 
            a[i][i] = 1;
        }
    }
    void Init(){     
        memset(a, 0, sizeof(a));
    }
};
Matrix mul(Matrix a, Matrix b){ 
    Matrix ans;
    for(int i=0;i<maxn;++i){ 
        for(int j=0;j<maxn;++j){ 
            ans.a[i][j] = 0;
            for(int k=0;k<maxn;++k){ 
                ans.a[i][j] += a.a[i][k] * b.a[k][j];
                ans.a[i][j] %= mod; 
            }
        }
    } 
    return ans;
}
Matrix qpow(Matrix a, ll n){ 
    Matrix ans;
    ans.init();
    while(n){ 
        if(n&1) ans = mul(ans, a);
        a = mul(a, a);
        n /= 2;
    } 
    return ans;
}
void output(Matrix a){ 
    for(int i=0;i<maxn;++i){ 
        for(int j=0;j<maxn;++j){ 
            cout << a.a[i][j] << " ";
        }
        cout << endl;
    }
}
int main(int argc, char const *argv[])
{ 
    ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    Matrix tmp;
    tmp.Init();
    tmp.a[0][0] = 1;
    tmp.a[0][1] = 1; 
    tmp.a[1][0] = 2;
    tmp.a[2][0] = 1;
    tmp.a[2][2] = 1;
    tmp.a[3][2] = 1;
    tmp.a[3][3] = 1;
    tmp.a[4][2] = 1;
    tmp.a[4][3] = 2;
    tmp.a[4][4] = 1;
    tmp.a[5][2] = 1;
    tmp.a[5][3] = 3;
    tmp.a[5][4] = 3;
    tmp.a[5][5] = 1;
    cin >> T;
    while(T--)
    { 
        cin >> n;
        Matrix t = qpow(tmp,n-2);
        //output(t);
        Matrix ans;
        ans.Init();
        ans.a[0][0] = 2;
        ans.a[0][1] = 1;
        ans.a[0][2] = 3*3*3;
        ans.a[0][3] = 3*3*3;
        ans.a[0][4] = 3*3;
        ans.a[0][5] = 1;
        Matrix as = mul(ans,t);
        cout << as.a[0][0] << endl;
    }
    return 0;
}