自编码器AutoEncoder

绝地灬酷狼 2021-10-15 10:29 905阅读 0赞

文章目录

    • 一. 什么是自编码器
    • 二. 有什么作用
      • 1) 图像去噪
      • 2) 可视化降维
    • 三. 如何实现
      • 1) 全连接层实现
      • 2) 测试: 对有噪声图像的自编码
      • 3) 卷积层实现
    • 四. 一些小细节

一. 什么是自编码器

自动编码器 autoencoder, 简单表现编码器为将一组数据进行压缩编码(降维), 解码器将这组数据恢复成高维的数据. 这种编码和解码的过程不是无损的, 因此最终的输出和输入是有一些差异的, 且非常依赖于训练的数据集.

如图所示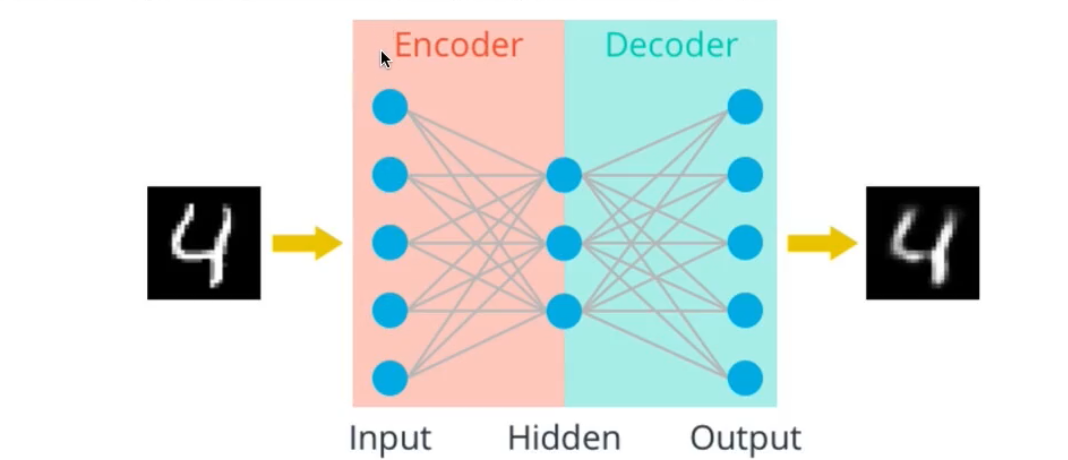
在这里插入图片描述

如上面这张图所示, 对于一个简单的三层线性神经网络组成的自编码器, 我们在进行神经网络的搭建过程中, 将(input, hidden) 这个过程叫做编码器, 将(hidden, output) 这个过程叫做解码器. 对于mnist数据集而言, 它的维度变化是 784 -> x -> 784, 其中, x < 784, 是编码的维度.

二. 有什么作用

1) 图像去噪

看上去很强啊
在这里插入图片描述

2) 可视化降维

三. 如何实现

训练神经网络需要定义损失函数, 那么这个自编码器的损失衡量值是什么?

衡量损失的值是由网络的输出结果和输入决定的. 也就是说, 是由这两个784维数据的差别决定的.

1) 全连接层实现

首先定义一个神经网络

  1. class Autoencoder(nn.Module):
  2.     def __init__(self, encoding_dim):
  3.         super(Autoencoder, self).__init__()
  4.         ## encoder ##
  5.         self.encoder = nn.Linear(784, encoding_dim)
  7.         ## decoder ##
  8.         self.decoder = nn.Linear(encoding_dim, 784)
  11.     def forward(self, x):
  12.         # define feedforward behavior 
  13.         # and scale the *output* layer with a sigmoid activation function
  14. # print(x.shape)
  15.         x = x.view(-1, 784)
  16.         x = F.relu(self.encoder(x))
  17.         x = torch.sigmoid(self.decoder(x))
  18.         return x
  20. # initialize the NN
  21. encoding_dim = 128
  22. model = Autoencoder(encoding_dim)

定义损失函数和优化器

  1. # specify loss function
  2. criterion = nn.MSELoss()
  4. # specify loss function
  5. optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

训练过程, 一共20个epochs, 话说pytorch还真慢, 这么简单的网络都要训练好一会

  1. # number of epochs to train the model
  2. n_epochs = 20
  4. for epoch in range(1, n_epochs+1):
  5.     # monitor training loss
  6.     train_loss = 0.0
  8.     ###################
  9.     # train the model #
  10.     ###################
  11.     for data in train_loader:
  12.         # _ stands in for labels, here
  13.         images, _ = data
  14.         # flatten images
  15.         images = images.view(images.size(0), -1)
  16.         # clear the gradients of all optimized variables
  17.         optimizer.zero_grad()
  18.         # forward pass: compute predicted outputs by passing inputs to the model
  19. # print(images.shape)
  20.         outputs = model(images)
  21.         # calculate the loss
  22.         loss = criterion(outputs, images)
  23.         # backward pass: compute gradient of the loss with respect to model parameters
  24.         loss.backward()
  25.         # perform a single optimization step (parameter update)
  26.         optimizer.step()
  27.         # update running training loss
  28.         train_loss += loss.item()*images.size(0)
  30.     # print avg training statistics 
  31.     train_loss = train_loss/len(train_loader)
  32.     print('Epoch: {} \tTraining Loss: {:.6f}'.format(
  33.         epoch, 
  34.         train_loss
  35.         ))

训练过程的损失变化

  1. Epoch: 1     Training Loss: 0.342308
  2. Epoch: 2     Training Loss: 0.081272
  3. Epoch: 3     Training Loss: 0.058724
  4. Epoch: 4     Training Loss: 0.051274
  5. Epoch: 5     Training Loss: 0.047382
  6. Epoch: 6     Training Loss: 0.044760
  7. Epoch: 7     Training Loss: 0.043184
  8. Epoch: 8     Training Loss: 0.042066
  9. Epoch: 9     Training Loss: 0.041246
  10. Epoch: 10     Training Loss: 0.040589
  11. Epoch: 11     Training Loss: 0.040059
  12. Epoch: 12     Training Loss: 0.039646
  13. Epoch: 13     Training Loss: 0.039272
  14. Epoch: 14     Training Loss: 0.038980
  15. Epoch: 15     Training Loss: 0.038733
  16. Epoch: 16     Training Loss: 0.038524
  17. Epoch: 17     Training Loss: 0.038328
  18. Epoch: 18     Training Loss: 0.038162
  19. Epoch: 19     Training Loss: 0.038012
  20. Epoch: 20     Training Loss: 0.037874

那么效果如何呢? 上面一排是输入图像, 下面一排是输出图像. 经过自编码器之后, 还原度还是很高的.

在这里插入图片描述

2) 测试: 对有噪声图像的自编码

首先查看一张图片

  1. a_img = np.squeeze(images[0])
  2. print(a_img.shape)
  3. print(np.max(a_img))
  4. print(np.min(a_img))
  6. plt.imshow(a_img, cmap='gray')

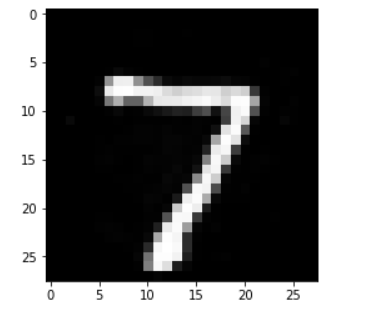
在这里插入图片描述
然后向其中加入噪声

  1. a_img_x = a_img + 0.08 * np.random.normal(loc=0.0, scale=1.0, size=a_img.shape)
  3. plt.imshow(a_img_x, cmap='gray')

这是加入噪声之后的图片, 可以看出差别还是很大的. 那么我们的编码器能还原出如何的效果呢?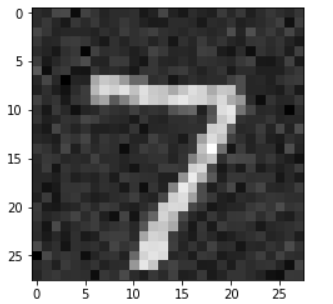
在这里插入图片描述

  1. a_img_output = model(torch.Tensor(a_img_x).view(1, -1))
  2. print(a_img_output.shape)
  4. output_img = a_img_output.view(28, 28)
  5. output_img = output_img.detach().numpy()
  7. plt.imshow(output_img, cmap='gray')

这是还原后的, 说实话看到这个图片我心里也是很惊讶的. 就在于加入那么多噪声之后, 居然还可以还原的如此清晰. 当然这是对于MNIST数据集而言, 这个数据集比较简单.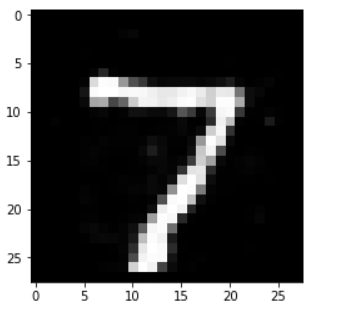
在这里插入图片描述

3) 卷积层实现

不同之处在于定义自编码器的神经网络结构
如图所示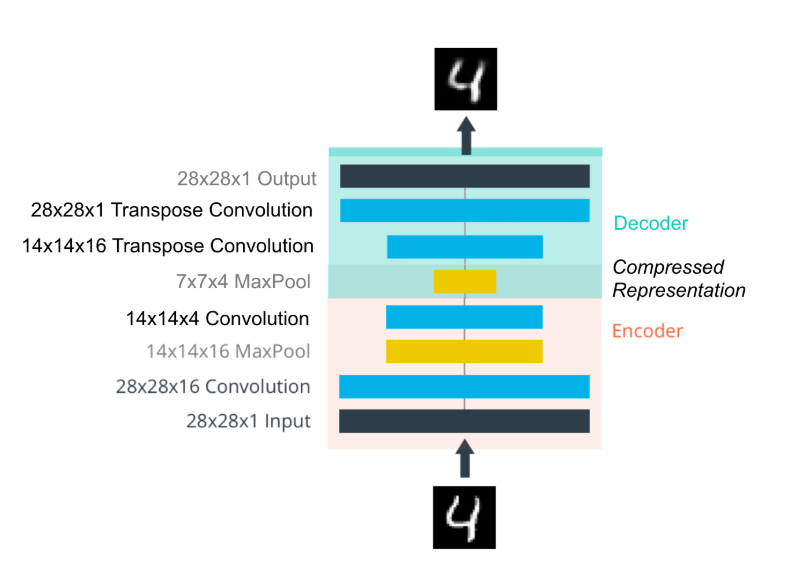
在这里插入图片描述
可以看到在decoder中经过了两个反卷积层, 但是由于水平有限, 这个反卷积层看着好奇怪, 不知道是怎么反卷积的.

pytorch实现

  1. import torch.nn as nn
  2. import torch.nn.functional as F
  4. # define the NN architecture
  5. class ConvAutoencoder(nn.Module):
  6.     def __init__(self):
  7.         super(ConvAutoencoder, self).__init__()
  8.         ## encoder layers ##
  9.         self.conv1 = nn.Conv2d(1, 16, 3, padding=1)
  10.         self.conv2 = nn.Conv2d(16, 4, 3, padding=1)
  12.         self.pool = nn.MaxPool2d(2, 2)        
  14.         ## decoder layers ##
  15.         ## a kernel of 2 and a stride of 2 will increase the spatial dims by 2
  16.         self.t_conv1 = nn.ConvTranspose2d(4, 16, 2, stride=2)
  17.         self.t_conv2 = nn.ConvTranspose2d(16, 1, 2, stride=2)
  20.     def forward(self, x):
  21.         ## encode ##
  23.         ## decode ##
  24.         ## apply ReLu to all hidden layers *except for the output layer
  25.         ## apply a sigmoid to the output layer
  26.         x = F.relu(self.conv1(x))
  27.         x = self.pool(x)
  28.         x = F.relu(self.conv2(x))
  29.         x = self.pool(x)
  31.         x = F.relu(self.t_conv1(x))
  32.         x = torch.sigmoid(self.t_conv2(x))
  34.         return x
  36. # initialize the NN
  37. model = ConvAutoencoder()
  38. print(model)

训练起来比全连接层的网络还要慢很多, 而损失值的降低也慢很多, 不像之前从epoch 1 到 epoch 2 直接就断崖式下跌了. 下面是损失值的变化过程, 只训练了 15个epoch. 从损失之上看这个效果好像差很多?

  1. Epoch: 1     Training Loss: 0.448799
  2. Epoch: 2     Training Loss: 0.266815
  3. Epoch: 3     Training Loss: 0.251290
  4. Epoch: 4     Training Loss: 0.240823
  5. Epoch: 5     Training Loss: 0.231836
  6. Epoch: 6     Training Loss: 0.220550
  7. Epoch: 7     Training Loss: 0.210341
  8. Epoch: 8     Training Loss: 0.202768
  9. Epoch: 9     Training Loss: 0.197010
  10. Epoch: 10     Training Loss: 0.193259
  11. Epoch: 11     Training Loss: 0.190589
  12. Epoch: 12     Training Loss: 0.188406
  13. Epoch: 13     Training Loss: 0.186529
  14. Epoch: 14     Training Loss: 0.184983
  15. Epoch: 15     Training Loss: 0.183579

观察下图的数字9的话, 可以看到损失了不少.
在这里插入图片描述

再看看噪声图片的处理能力如何

原图: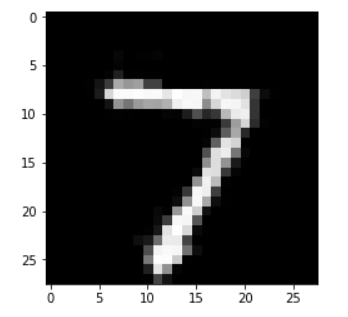
在这里插入图片描述
加入噪声: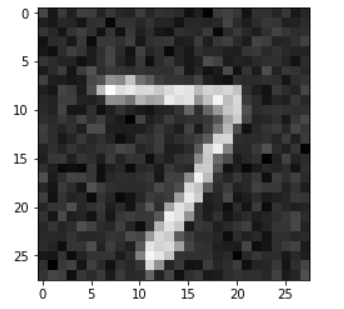
在这里插入图片描述
经过自编码器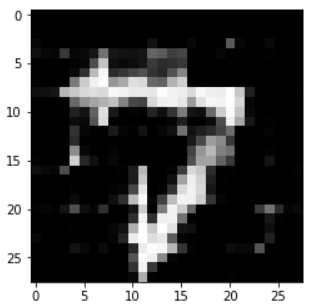
在这里插入图片描述
呃, 效果似乎有点不是很对, 可能是训练的epoch太少了, 毕竟我们可以前面看到训练15个epoch的损失值还是达到了0.18, 而在全连接层的简单自编码器上第二个epoch的损失值就达到了0.08

另一张图片

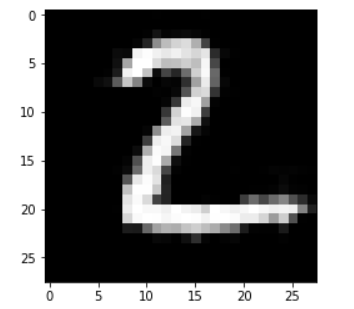
在这里插入图片描述
噪声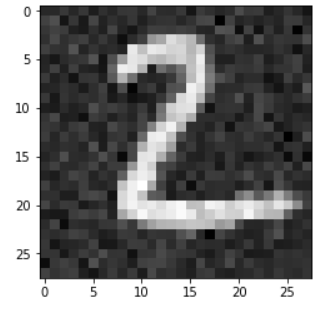
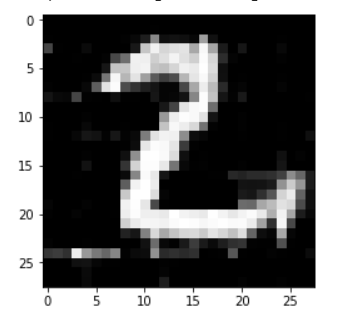
在这里插入图片描述
在这里插入图片描述

四. 一些小细节

  1. numpy 的 squeeze 函数
    参考博客
    作用：从数组的形状中删除单维度条目，即把shape中为1的维度去掉

  2. 给MNIST图片加入噪声的方法

    test_img_x = test_img + 0.08 * np.random.normal(loc=0.0, scale=1.0, size=test_img.shape)

就是加入一些随机值, 在原图的基础上进行小幅度修改.

发表评论

表情：
评论列表 （有 0 条评论，905人围观）

还没有评论，来说两句吧...

相关阅读