#笔记整理
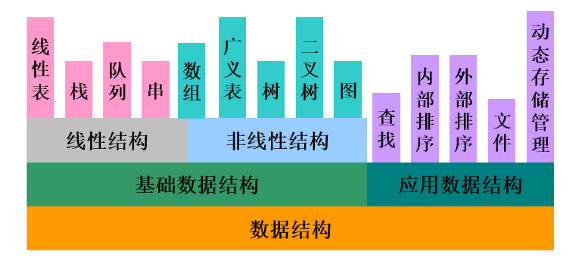
在这里插入图片描述

查找

查找的基本概念
静态查找表——基于线性表的查找法（二分查找）
动态查找表——基于树表的查找法（二叉排序树、平衡二叉树、B树、红黑树）
哈希表——计算式查找法

动态查找表——基于树表的查找法

动态查找表的特点：
表结构本身在查找过程中动态生成，即对于给定值 key，若表中存在关键字等于 key 的记录，则查找成功，否则插入关键字等于 key 的记录。

动态查找表的主要运算
- 创建、销毁
- 查找、插入和删除
- 遍历

二叉排序树（二叉搜素树、二叉查找树）BST (Binary Sort Tree)/(Binary Search Tree)

定义：
二叉排序树或者是一棵空树，或者是具有如下性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于根结点的值；
它的左右子树也分别为二叉排序树。

二叉排序树的查找操作

二叉排序树可看做是一个有序表，在二叉排序树上进行查找,和折半查找类似,也是一个逐步缩小查找范围的过程。

// 二叉树结点结构的定义
typedef struct BiTNode{
    int data;
    BiTNode *lchild, *rchild;
    BiTNode(int n = 0) : data(n), lchild(nullptr), rchild(nullptr){
    }
}BiTNode, *BiTree;
// 二叉排序树的查找操作，递归查找二叉排序树 T 中是否存在 key
// parent 指向 T 的双亲
// p 指向查找成功的结点或指向查找路径上访问的最后一个结点。
bool searchBST(BiTree T, int key, BiTNode *parent, BiTNode **p){
    if(!T){
                        // 树遍历结束都没有找到 key， 查找失败。
        *p = parent;
        return false;
    }else if(key == T->data){
      // 查找成功
        *p = T;
        return true;
    }else if(key < T->data){
        return searchBST(T->lchild, key, T, p);
    }else{
        return searchBST(T->rchild, key, T, p);
    }
}

二叉排序树的插入操作（创建二叉排序树）

插入操作的特点：

二叉排序树的生成,是从一个空树开始,每插入一个关键字,就调用一次插入算法将它插入到当前已生成的二叉排序树中；
新插入的结点一定是一个新的叶子结点；中序遍历二叉排序树，得到一个关键字有序序列（树排序）；
二叉排序树的形态完全由一个输入序列确定；

示例：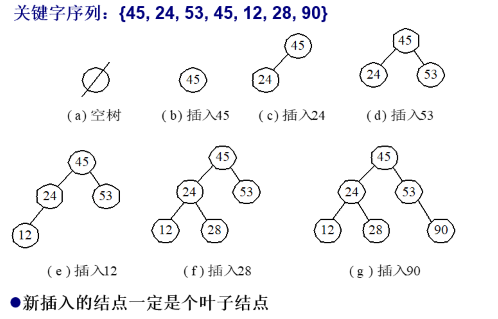
在这里插入图片描述

// 二叉排序树的插入操作1，使用 searchBST 实现
    // 当二叉排序树 T 中不存在关键字等于 key 的元素时插入 key 并返回 true，否则返回 false
    bool insertBST(BiTree *T, int key){
        BiTNode *p;
        if(!searchBST(*T, key, NULL, &p)){
      // 若 key 不存在树中，则插入
            BiTNode *new_node = new BiTNode(key);
            if(!p){
                             // 树为空，则 T 应为根结点
                *T = new_node;
            }else if(key < p->data){
            // 插入左子树
                p->lchild = new_node;
            }else{
                              // 插入右子树
                p->rchild = new_node;
            }
            return true;
        }else{
            return false;
        }
    }
    // 二叉排序树的插入操作2，使用递归实现
    // 当二叉排序树 T 中不存在关键字等于 key 的元素时插入 key 并返回 true，否则返回 false
    bool insertBST2(BiTree *T, int key){
        if(!(*T)){
            BiTNode *new_node = new BiTNode(key);
            *T = new_node;
            return true;
        }else if(key < (*T)->data){
             // 插入左子树
            insertBST2( &(*T)->lchild, key);
        }else if(key > (*T)->data){
             // 插入右子树
            insertBST2( &(*T)->rchild, key);
        }else{
                                  // 存在相同元素
            return false;
        }
    }

二叉排序树的删除操作：

在二叉排序树中删去一个结点相当于删去有序序列中的一个结点。
设要删除的结点为 p，结点 p 的双亲结点为 f。
分 3 种情况讨论：（代码以 C 语言为例）

若 p 为叶子结点，则可直接将其删除:

f->rchild = NULL (或 f->lchild = NULL) ；
```
 free(p)；
```

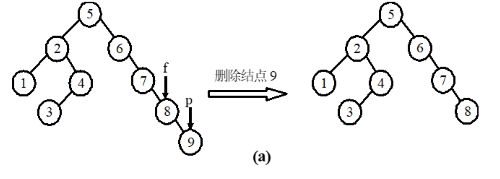
在这里插入图片描述

若 p 结点只有左子树，或只有右子树，则可将 p 的左子树或右子树直接改为其双亲结点f的左(右)子树，即：

f->rchild = p->lchild（或 f->rchild = p->rchild）；
```
 free(p)；
```

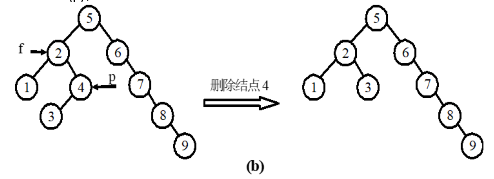
在这里插入图片描述

若 p 既有左子树，又有右子树，假设 p 为双亲 f 的左孩子。此时有两种处理方法：
方法1：将 p 的左子树改为 f 的左子树，而将 p 的右子树改为 s 的右子树。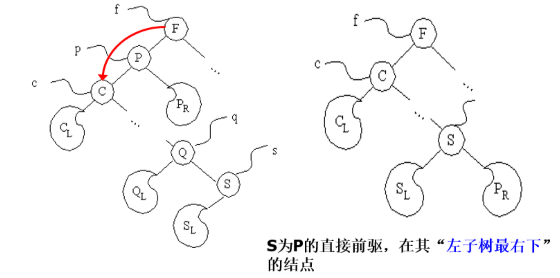
在这里插入图片描述
方法2：用 s 结点的值替代 p 结点的值，再将 s 结点删除，原 s 结点的左子树改为 s 的双亲结点 q 的右子树。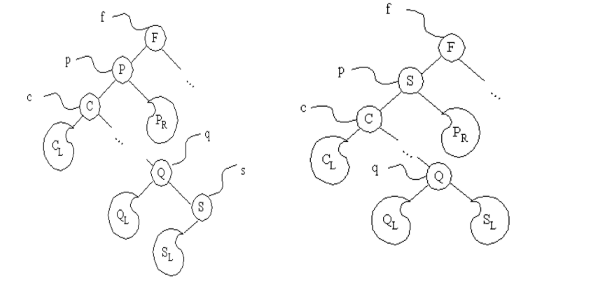

C++实现示例：

// 二叉排序树的删除操作

 // 递归查找，若二叉排序树中存在与 key 值相等的结点，则将其删除并返回 true ，否则返回 false;
 bool deleteBST(BiTree *T, int key){
     if(!*T){
         return false;
     }else{
         if( (*T)->data == key){
                      // 若当前结点值和 key 相等，则删除
             return deleteNode(T);
         }else if(key < (*T)->data){
             return deleteBST(&(*T)->lchild, key);   // 查找左子树
         }else{
             return deleteBST(&(*T)->rchild, key);   // 查找右子树
         }
     }
 }
 // 从二叉排序树中删除 p 结点，并重接它的左右子树
 // 使用方法2，用 s 结点的值替代 p 结点的值，再将 s 结点删除，原 s 结点的左子树改为 s 的父结点 q 的右子树。
 bool deleteNode(BiTree *p){
     BiTree q, s;
     if((*p)->lchild == nullptr){
         // 只有右子树的时候，直接重连右子树
         q = *p;
         *p = (*p)->rchild;
         delete(q);
     }else if((*p)->rchild == nullptr){
   // 只有左子树的时候，直接重连左子树
         q = *p;
         *p = (*p)->lchild;
         delete(q);
     }else{
                               // 左右子树都不为空
         q = *p;
         s = (*p)->lchild;
         while(s->rchild){
                // 转左，并向右走到尽头（即找到待删结点的前驱）
             q = s;
             s = s->rchild;
         }
         (*p)->data = s->data;           // 用 s 结点的值替代 p 结点的值
         if(q != *p){
             q->rchild = s->lchild;
         }else{
             q->lchild = s->lchild;
         }
         delete(s);
     }
 }

二叉排序树的查找分析

若查找成功，则走了一条从根结点到某结点的路径，若查找失败，则走到一棵空的子树时为止。因此，最坏情况下，其平均查找长度不会超过树的高度。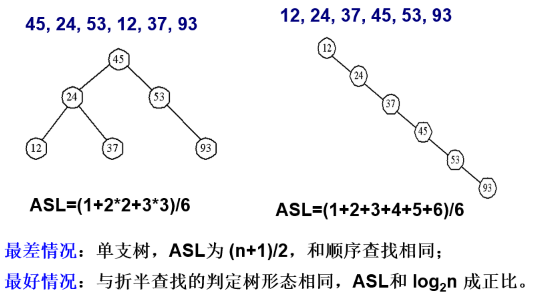
在这里插入图片描述

平衡二叉树（self-balancing binary search tree 或 height-balanced binary search tree）

定义：
平衡二叉树、平衡二叉搜索树，最早的平衡二叉树之一。
每个结点的左子树和右子树的高度差至多等于 1 的一种二叉排序树。
由于两位俄罗斯数学家 G.M.Adelson-Velskii 和 E.M.Landis 在1962年共同发明一种解决平衡二叉树的算法，因此平衡二叉树也称为 AVL 树。
相对其他数据结构，AVL 树实际应用的场景比较少。windows对进程地址空间的管理用到了 AVL 树。

平衡因子 BF(Balance Factor) ：
二叉树中每个结点的平衡因子是该结点左子树的高度减去右子树的高度。

从平衡因子的角度可以说，若一棵二叉树中所有结点的平衡因子的绝对值小于或等于 1，即平衡因子取值为 1、0 或 -1，则该二叉树称为平衡二叉树。

在一个平衡二叉排序树上插入一个新结点S时，主要包括以下三步：