【数据结构】树：哈夫曼树（Huffman Tree，也称哈弗曼、赫夫曼树）、哈夫曼编码解析与实现（c++）-蒲公英云

#笔记整理

树的定义参照前文：
二叉树、遍历二叉树与线索二叉树等树的定义与解析、二叉树遍历实现

哈夫曼树（也称赫夫曼树）

哈夫曼树(最优二叉树)

具有最小带权路径长度的二叉树称为哈夫曼树。
如下图 ( c )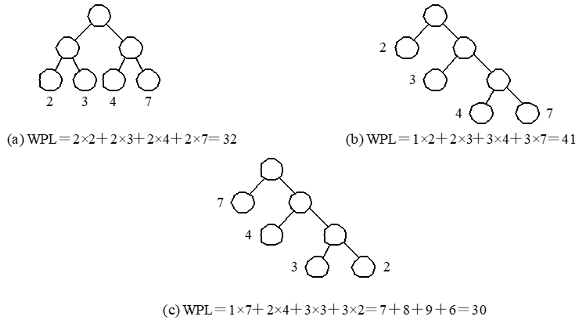
在这里插入图片描述

构建哈夫曼树（哈夫曼算法）

由给定的n个权值 W 1 , W 2 , . . . , W n {W1,W2,…,Wn} W1,W2,…,Wn,构造 n 棵只有一个结点的二叉树，从而得到一个二叉树的集合 F = T 1 , T 2 , . . . , T n F={T1,T2,…,Tn} F=T1,T2,…,Tn;
在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树，这棵新的二叉树根结点的权值为其左、右子树根结点权值之和;
在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中;
重复(2)、(3)两步，当F中只剩下一棵二叉树时，这棵二叉树便是所要建立的赫夫曼树。

示例：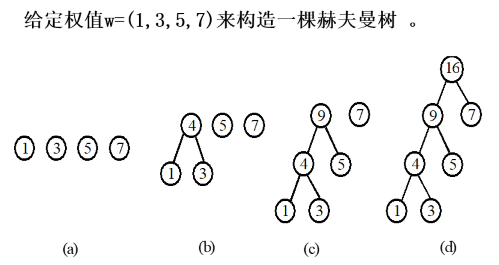
在这里插入图片描述

哈夫曼树中没有度为 1 的结点（可称为严格的（或正则的）二叉树），因此一棵有 n 个叶子节点的哈夫曼树一共有 2n - 1 个结点，可以存储在一个大小为 2n - 1 的一维数组中。

算法实现：

// 创建哈夫曼树 hTree
void createHuffTree(vector<HuffTreeNode> &hTree){
    int n, s1, s2, len;
    char c;     // 字符
    int weight; // 字符权值
    cout << "请输入字符集大小（即叶子数）：" << endl;
    cin >> n;
    len = 2 * n - 1;  // 哈夫曼树的结点数
    hTree.resize(len);
    cout << n << "个字符及其的权值是：(输入格式如：a1 b5 d23，空格分隔)" << endl;
    for(int i = 0; i < n; i++){
        cin >> c >> weight;
        hTree[i].data   = c;
        hTree[i].weight = weight;
        hTree[i].parent = -1;
        hTree[i].left   = -1;
        hTree[i].right  = -1;
    }
    for(int i = n; i < len; i++){
        hTree[i].parent = -1;                                   // vector中的其余结点的双亲域初始化为 -1
    }
    cout << endl << "------------------开始创建哈夫曼树------------------" << endl << endl;
    for(int i = n; i < len; i++){
                                   // 创建哈夫曼树
        select(hTree, i, s1, s2);                               // 选出当前没有双亲的最小和次小的结点
        hTree[s1].parent = hTree[s2].parent = i;                // 设置当前 i 为选出的结点的双亲结点
        hTree[i].left    = s1;                                  // 设置结点 i 的左右孩子
        hTree[i].right   = s2;
        hTree[i].weight  = hTree[s1].weight + hTree[s2].weight; // 双亲结点的权值为两孩子结点权值之和
    }
    cout << "------------------哈夫曼树创建完成------------------" << endl;
}
// 返回哈夫曼树前 i 个结点中权值最小和次小的两棵树的根结点序号 s1 和 s2，并创建该俩结点的双亲结点
void select(vector<HuffTreeNode> &hTree, int i, int &s1, int &s2){
    int j, m;
    for(j = 0; j < i && hTree[j].parent != -1; j++);                           // 找到第一个可能的根结点
    s1 = j;
    for(j = s1 + 1; j < i && hTree[j].parent != -1; j++);                      // 找到第二个可能的根结点
    s2 = j;
    if(hTree[s1].weight > hTree[s2].weight){
                                       // 若第二个结点的权值小于第一个结点，交换俩结点
        int temp = s1;
        s1 = s2;
        s2 = temp;
    }
    for(m = j + 1; m < i; m++){
        if(hTree[m].parent == -1 && hTree[m].weight < hTree[s1].weight){
            // 若还有比 s1 的权值更小的结点，交换 s1、s2和m
            s2 = s1;
            s1 = m;
        }else if(hTree[m].parent == -1 && hTree[m].weight < hTree[s2].weight){
      // 若还有只比 s2 的权值小的结点，只需交换 s2 和 m
            s2 = m;
        }
    }
}

哈夫曼编码（也称赫夫曼编码）

相关概念：
前缀编码：任一字符的编码都不是另一个字符的编码的前缀。
使用前缀编码能设计出长短不等的编码。
如：
a：000
b：001
c：01
d：1
编码对应的哈夫曼树：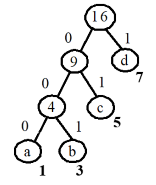
在这里插入图片描述
在进行数据通讯时，涉及数据编码问题。所谓数据编码就是将信息原文转换为二进制字符串，译码则是将信息的编码形式转换为原文。
常规的编码会让转换成的二进制序列很长，因为每个字符对应的二进制值长度几乎都是固定的，因此需要使用哈夫曼编码来进行改进，哈夫曼编码能根据字符出现的频率（即权值）来生成每个字符所对应的二进制值，频率越高二进制值长度越短，这样最终哈夫曼编码的编码结果就比常规编码要短很多，从而达到了数据压缩的效果。

哈夫曼编码： 设需要编码的字符集为 c 1 , c 2 , … , c n {c_1, c_2, … , c_n} c1,c2,…,cn ，各个字符在电文中出现的次数或频率集合为 w 1 , w 2 , … , w n {w_1, w_2, …, w_n} w1,w2,…,wn ，以 c 1 , c 2 , … , c n c_1, c_2, …, c_n c1,c2,…,cn作为叶子结点，以 w 1 , w 2 , … , w n w_1, w_2, …, w_n w1,w2,…,wn 作为叶子结点的权值，来构造一棵哈夫曼树。规定哈夫曼树的左分支代表 0，右分支代表 1，则从根结点到叶子结点所经过的路径分支组成的 0 和 1 的序列，便是该结点对应字符的编码，这就是哈夫曼编码。
算法实现：

// 从根到叶子，求每一个字符的哈夫曼编码
// hTree：建好的哈夫曼树， n : 叶子结点数
void huffmanCodingLeaf(vector<HuffTreeNode> &hTree, int n){
    string str = "";
    string *hCode = new string[n];              // 分配 n 个字符串数组，用于存放每个字符的编码
    assert(hCode != NULL);
    vector<int> nodeStatus(hTree.size(), 0);    // 哈夫曼树中每个结点的状态容器，初始为0，表示左右孩子未被访问过
    int i = hTree.size() - 1;                   // i 指向根结点
    while(i >= 0){
        if(nodeStatus[i] == 0){
                     // 当前结点的左右孩子都未被访问过
            nodeStatus[i] = 1;                  // 从左孩子开始，1 表示左孩子已被访问
            if(hTree[i].left > -1){
                 // 有左孩子
                i = hTree[i].left;
                str += '0';                     // 在尾部添加编码 0
            }else{
                                  // 没有左孩子，即为叶子结点
                hCode[i] = str;                 // 该字符编码结束，存储该字符的编码
                i = hTree[i].parent;            // 退回该字符的父结点
                str.erase(str.size() - 1, 1);   // 初始化 str
            }
        }else if(nodeStatus[i] == 1){
               // 左孩子已访问过，右孩子不曾被访问
            nodeStatus[i] = 2;                  // 左右孩子都被访问过的标志
            i = hTree[i].right;
            str += '1';                         // 串尾追加编码1
        }else{
                                      // 左右孩子都被访问过
            i = hTree[i].parent;
            if(i >= 0){
                             // 根结点没有父结点，不加此判断会产生访问越界错误
               str.erase(str.size() - 1, 1);    // 初始化字符串
            }
        }
    }
    cout << endl << "-----------------------编码完成---------------------" << endl << endl;
    cout << "每个字符的编码为：" << endl;
    for(int j = 0; j < n; j++){
        cout << hTree[j].data << " : " <<  hCode[j] << endl;
    }
    delete[] hCode;
}

查看源码与其中的注释，或许更容易理解
github源码

实现结果：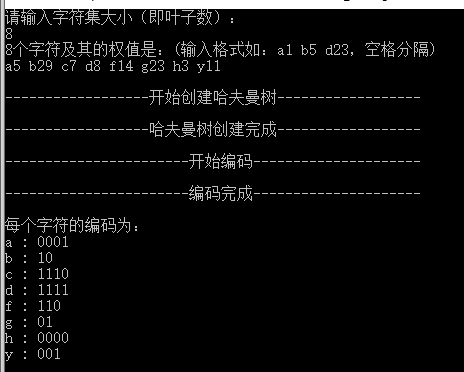
在这里插入图片描述

整理与总结的时候翻到了自己2014年写的哈夫曼编译器，当时还是大二，哈夫曼编译器是老师布置的一项作业，重新看了一下当时写的代码和作业报告，心里不由得微微一笑，看到了自己当初的稚嫩。报告如下图，整个编译器源码也已上传到github上了，我只添加了一点注释，其他原封未动，仅留作纪念。（当时的报告竟然叫实习报告，也是挺好笑的哈哈）

在这里插入图片描述