线性排序原理及其实现 counting sort

喜欢ヅ旅行 2021-12-14 01:47 237阅读 0赞

转载自：[https://www.cnblogs.com/onepixel/articles/7674659.html][https_www.cnblogs.com_onepixel_articles_7674659.html]

# 计数排序 #

计数排序不是基于比较的排序算法，其核心在于将输入的数据转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是**有确定范围的整数**。

### 算法描述 ###

1、找出待排序的数组中的最大和最小元素。  
2、统计数组中每个值为i的元素出现的次数，存入数组b的第i项。  
3、对所有的计数累加（从b的第一个元素开始，每一项和前一项相加）  
4、反向填充目标数组：将每个元素i放在新数组的第b（i）项，每放一个元素就将b(i)减去1。

### 代码实现 ###

//计数排序
        public int[] countSort(int a[]){
            int b[] = new int[18];//数字范围为0到17
            int c[] = new int[18];
            for (int i = 0;i<a.length;i++){
                b[i]=0;
            }
            for (int i = 0;i <a.length;i++){
                b[a[i]]++;//元素出现了多少次
            }
            for (int i = 1;i < a.length;i++){
                b[i] = b[i]+b[i-1];
            }
            for (int i = a.length-1;i >=0;i--){
                c[b[a[i]]]=a[i];//反向填充到c数组中
                b[a[i]]--;
            }
            return c;
        }

*  1
 *  2
 *  3
 *  4
 *  5
 *  6
 *  7
 *  8
 *  9
 *  10
 *  11
 *  12
 *  13
 *  14
 *  15
 *  16
 *  17
 *  18
 *  19

### 算法分析 ###

计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)，其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。

# 桶排序 #

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。  
工作原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或者是以递归方式继续使用桶排序进行排）

### 算法描述 ###

1、设置一定数量的数组当做空桶  
2、遍历输入数据，吧数据通过映射函数一个一个放到对应的桶里去。  
3、对每个不是空的桶进行排序  
4、从不是空的桶里把排好序的数据拼接起来。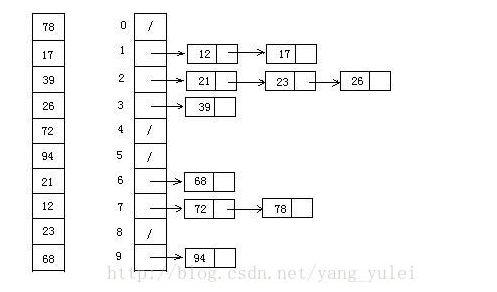  
![这里写图片描述][70]

### 代码实现 ###

public int [] BucketSort(int a[]){
            int minValue = a[0];
            int maxValue = a[0];
            for (int i = 1;i<a.length;i++){
                if (a[i] < minValue){
                    minValue = a[i];
                }
                if (a[i] > maxValue){
                    maxValue = a[i];
                }
            }
            int bucketSize = 3;//把桶的数量设置为3个
            int step = (maxValue-minValue)/bucketSize + 1;
            List<ArrayList<Integer>> buckets = new ArrayList<>();
            buckets.add(0,new ArrayList<>());
            buckets.add(1,new ArrayList<>());
            buckets.add(2,new ArrayList<>());
            for (int i = 0;i<a.length;i++){//设置映射函数
                buckets.get((a[i] - minValue)/step).add(a[i]);
            }
    
            int d[] = new int[a.length];//将最终排序结果放在d里面
            int f = 0;
            for (int i = 0;i<buckets.size();i++){//对每个桶执行插入排序
                int c[] = new int[buckets.get(i).size()];
                for (int b = 0;b<buckets.get(i).size();b++){
                    c[b] = buckets.get(i).get(b);
                }
                InsertSort(c);
                for (int e = 0;e<c.length;e++){
                    d[f]= c[e];//数据拼接
                    f++;
                }
            }
            return d;
        }

*  1
 *  2
 *  3
 *  4
 *  5
 *  6
 *  7
 *  8
 *  9
 *  10
 *  11
 *  12
 *  13
 *  14
 *  15
 *  16
 *  17
 *  18
 *  19
 *  20
 *  21
 *  22
 *  23
 *  24
 *  25
 *  26
 *  27
 *  28
 *  29
 *  30
 *  31
 *  32
 *  33
 *  34
 *  35
 *  36

### 算法分析 ###

桶排序是稳定的排序算法。桶排序最好的情况下时间复杂度O(n)，桶排序的时间复杂度，取决于对各个桶之间的数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)，很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增加。

# 基数排序 #

基数排序是按照低位先排序，然后收集，然后再按照高位排序，然后收集；依次类推。直到最高位。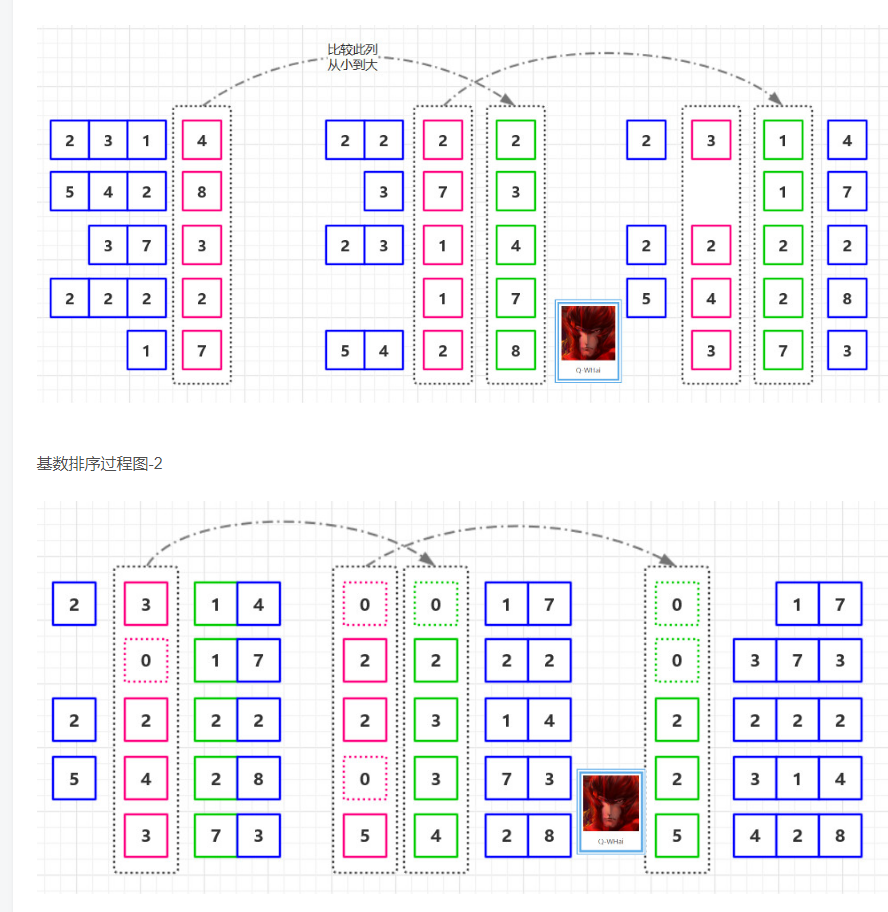  
![这里写图片描述][70 1]

### 代码实现 ###

public void RadixSort(int a[]){
            int maxDigit = a[0];
            for (int i = 1;i < a.length;i++){
                if (a[i] > maxDigit){
                    maxDigit = a[i];
                }
            }
    
            List<ArrayList<Integer>> buckets = new ArrayList<>();
            for (int i = 0;i< 10;i++){
                buckets.add(i,new ArrayList<>());
            }
            maxDigit = maxDigit * 10;
            int chu = 1;
            int index = 0;
            while (maxDigit  / 10 > 0){//先按照低位进行排序，然后再按照高位进行排序
                if (index == 0){
                    for (int i = 0;i<a.length;i++){
                        int mod = a[i] / chu;
                        mod = mod % 10;
                        buckets.get(mod).add(a[i]);//放到对应的桶中
                    }
    
                }else {
    
                    for (int i = 0;i<buckets.size();i++){
                        int size = buckets.get(i).size();
                        for (int b = 0;b < size;b++){
                            int number = buckets.get(i).get(0);
                            int mod = number / chu;
                            mod = mod % 10;
                            buckets.get(i).remove(0);//调整元素所在桶的位置
                            buckets.get(mod).add(number);
                        }
                    }
                }
                maxDigit = maxDigit /10;
                chu = chu * 10;
                index++;
            }
    
            int c = 0;
            for (int i = 0;i<buckets.size();i++){
                for (int b = 0;b < buckets.get(i).size();b++){
                    a[c] = buckets.get(i).get(b);
                    c++;
                }
            }
    
        }

*  1
 *  2
 *  3
 *  4
 *  5
 *  6
 *  7
 *  8
 *  9
 *  10
 *  11
 *  12
 *  13
 *  14
 *  15
 *  16
 *  17
 *  18
 *  19
 *  20
 *  21
 *  22
 *  23
 *  24
 *  25
 *  26
 *  27
 *  28
 *  29
 *  30
 *  31
 *  32
 *  33
 *  34
 *  35
 *  36
 *  37
 *  38
 *  39
 *  40
 *  41
 *  42
 *  43
 *  44
 *  45
 *  46
 *  47
 *  48
 *  49
 *  50

### 算法分析 ###

![这里写图片描述][70 2]

[https_www.cnblogs.com_onepixel_articles_7674659.html]: https://www.cnblogs.com/onepixel/articles/7674659.html
[70]: /images/20211213/b5165f3c8bd24c988f6dfcc62447628e.png
[70 1]: /images/20211213/409323976c584d1fa5239ab8a63cd0f3.png
[70 2]: /images/20211213/eafd4e87ea01488cb85135e3027d4576.png