Unique Binary Search Trees-蒲公英云

Unique Binary Search Trees

Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?

For example,
Given n = 3, there are a total of 5 unique BST’s.

1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

终于开始动态规划的题目了。这道题目需要耐心挖掘其中的规律，首先根不一样的二叉搜索树肯定是不同的搜索树。依次类推，如果根结点一样，但是根结点下的一层结点不一样，则也是不一样的二叉搜索树。只要叶子结点的上一层结点有结点不一样，则是不一样的二叉搜索树。依次类推。从n为0开始列举：

n = 0

n = 1

n = 2

1 2

 \\                /
  2            1

n = 3

1 3 3 2 1

\\        /     /       / \\       \\
 3    2    1      1   3      2
/     /        \\                    \\

2 1 2 3

定义f(n)为unique BST的数量，以n = 3为例：

构造的BST的根节点可以取{1, 2, 3}中的任一数字。

如以1为节点，则left subtree只能有0个节点，而right subtree有2, 3两个节点。所以left/right subtree一共的combination数量为：f(0) * f(2) = 2

以2为节点，则left subtree只能为1一个节点，right subtree只能为2个节点：f(1) * f(1) = 1

以3为节点，则left subtree有1, 2两个节点，right subtree有0个节点：f(2)*f(0) = 2

所以总结以上可以得出规律，f(n)=f(0)*(n－1）＋f(1)＊f(n-2)＋f(2)*f(n-3)+…..f(n-1)*f(0)为卡特兰数。

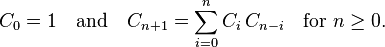
class Solution(object):
    def numTrees(self, n):
        """
        :type n: int
        :rtype: int
        """
        f = [0]*(n+1)
        f[0] = 1
        for i in xrange(1,n+1):
            for j in xrange(n):
                f [i] += f[j]*f[i-1-j]
        return f[n]