Algorithm | Tree traversal-蒲公英云

Algorithm | Tree traversal

There are three types of depth-first traversal: pre-order,in-order, and post-order.

For a binary tree, they are defined as operations recursively at each node, starting with the root node as follows:

Pre-order

Visit the root.
Traverse the left subtree.
Traverse the right subtree.

iterativePreorder(node)
  parentStack = empty stack
  parentStack.push(null)
  top =  node 
  while ( top != null )
      visit( top )
      if ( top.right != null ) 
          parentStack.push(top.right)
      if ( top.left != null ) 
          parentStack.push(top.left)
      top = parentStack.pop()

In-order

Traverse the left subtree.
Visit root.
Traverse the right subtree.

iterativeInorder(node)
  parentStack = empty stack
  while (not parentStack.isEmpty() or node ≠ null)
    if (node ≠ null)
      parentStack.push(node)
      node = node.left
    else
      node = parentStack.pop()
      visit(node)
      node = node.right

Post-order

Traverse the left subtree.
Traverse the right subtree.
Visit the root.

iterativePostorder(node)
  parentStack = empty stack  
  lastnodevisited = null 
  while (not parentStack.isEmpty() or node ≠ null)
    if (node ≠ null)
      parentStack.push(node)
      node = node.left
    else
      peeknode = parentStack.peek()
      if (peeknode.right ≠ null and lastnodevisited ≠ peeknode.right) 
        /* if right child exists AND traversing node from left child, move right */
        node = peeknode.right
      else
        parentStack.pop() 
        visit(peeknode)
        lastnodevisited = peeknode

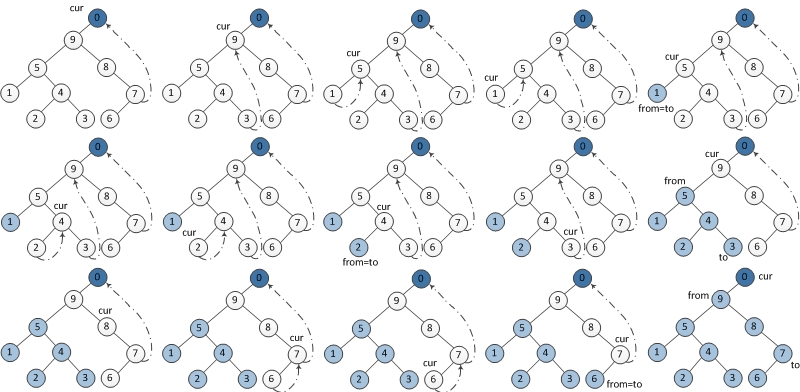
Morris Travel

1 /**
 2  * Definition for binary tree
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 8  * };
 9  */
10 class Solution {
11 public:
12     vector<int> inorderTraversal(TreeNode *root) {
13         vector<int> ret;
14         if (!root) return ret;
15         TreeNode *cur = root;
16         
17         while (cur) {
18             if (!cur->left) {
19                 ret.push_back(cur->val);
20                 cur = cur->right;
21             } else {
22                 TreeNode *rightmost = cur->left;
23                 while (rightmost->right != NULL && rightmost->right != cur) rightmost = rightmost->right;
24                 if (rightmost->right == cur) {
25                     rightmost->right = NULL;
26                     ret.push_back(cur->val);
27                     cur = cur->right;
28                 } else {
29                     rightmost->right = cur;
30                     cur = cur->left;
31                 }
32             }
33         }
34         
35         return ret;
36     }
37 };