KNN算法
1、kNN算法又称为k近邻分类(k-nearest neighbor classification)算法。
最简单平凡的分类器也许是那种死记硬背式的分类器,记住所有的训练数据,对于新的数据则直接和训练数据匹配,如果存在相同属性的训练数据,则直接用它的分类来作为新数据的分类。这种方式有一个明显的缺点,那就是很可能无法找到完全匹配的训练记录。
kNN算法则是从训练集中找到和新数据最接近的k条记录,然后根据他们的主要分类来决定新数据的类别。该算法涉及3个主要因素:训练集、距离或相似的衡量、k的大小。
下面通过一个简单的例子来看下

通过KNN算法算出唐人街探案是属于哪种类型的电影
过程:
(1)在进行KNN算法之前需要先进行数据清洗,如异常值,野值等会干扰结论(本案例数据较少可不用进行数据清洗)
(2)计算每个样本和新样本的相似度
公式:d= √(x-x1)^2+(x-x2)^2+(x-x3)^2
(3)对数据以相似度进行顺序排序
(3)选取k值,根据样本数据数量的大小取k值,本案中可取k=5,然后取5个样本数据中最多的标签(取众数)
代码如下
import pandas as pdimport numpy as npdata = pd.read_excel(r'C:\Users\Administrator\Desktop\电影分类数据.xlsx',encoding='gbk')print(data.columns)# 计算与表中每个电影的相似度并插入表中'相似性'字段data['相似度'] = np.sqrt((data.columns[7]-data['搞笑镜头'])**2+(data.columns[8]-data['拥抱镜头'])**2+(data.columns[9]-data['打斗镜头'])**2)# 对表中的数据以相似性进行顺序排序data.sort_values(by='相似度',inplace=True)print(data)result = data['电影类型'].head()print('{}属于'.format(data.columns[6]),result.mode()[0])
运行结果:
E:\Anaconda3\python.exe E:/Project/人工智能/day-05-27/KNN算法.pyIndex(['序号', '电影名称', '搞笑镜头', '拥抱镜头', '打斗镜头', '电影类型', '唐人街探案', 23, 3, 17], dtype='object')序号 电影名称 搞笑镜头 拥抱镜头 打斗镜头 电影类型 唐人街探案 23 3 17 相似度6 7 我的特工爷爷 6 4 21 动作片 NaN NaN NaN NaN 17.4928561 2 美人鱼 21 17 5 喜剧片 NaN NaN NaN NaN 18.5472373 4 功夫熊猫3 39 0 31 喜剧片 NaN NaN NaN NaN 21.4709110 1 宝贝当家 45 2 9 喜剧片 NaN NaN NaN NaN 23.4307492 3 澳门风云3 54 9 11 喜剧片 NaN NaN NaN NaN 32.14031710 11 新步步惊心 8 34 17 爱情片 NaN NaN NaN NaN 34.4383518 9 夜孔雀 9 39 8 爱情片 NaN NaN NaN NaN 39.6610649 10 代理情人 9 38 2 爱情片 NaN NaN NaN NaN 40.57092611 12 伦敦陷落 2 3 55 动作片 NaN NaN NaN NaN 43.4165874 5 谍影重重 5 2 57 动作片 NaN NaN NaN NaN 43.8748227 8 奔爱 7 46 4 爱情片 NaN NaN NaN NaN 47.6864765 6 叶问3 3 2 65 动作片 NaN NaN NaN NaN 52.009614唐人街探案属于 喜剧片Process finished with exit code 0
如果数据非常多的时候那么如何选定k值呢?
我们需要对k值进行训练,也就是选几组k值,对结果进行比对,准确率最高的就是最佳的k值
有两个文件夹,trainingDigits(训练集数据)和testDigits(测试集数据),每个文件夹中有上千个文件(0-1,0-2…..0-100,1-0,1-1…..),每个文件中有32*32个由1和0组成的数据形式,如图所示;

根据每个文件夹中的文件(0-1,0-2…..0-100,1-0,1-1…..),例如0-1,0-2……0-100文件中的数据就属于‘0’,1-0,1-1…..1-100文件属于’1’进行分类,根据trainingDigits(训练集数据)进行统一分类建模,用testDigits(测试集数据)进行测试。并选定k值
代码分为两部分,首先是对数据进行读取,并以同样的形式进行保存,代码如下:
import osimport pandas as pdimport numpy as npdef data_train(dirth):try:file_list = os.listdir(dirth)# (1)提取标签,从文件名上arr = np.zeros((len(file_list),1025))# (2)读文件夹中所有的txt文件for index,i in enumerate(file_list):biaoqian = i.split('_')[0]file_path =dirth+'/'+ifile_content = np.loadtxt(file_path,dtype=str)print('-------', file_content)# shux = ''.join(file_content)# shux1 = [int(a) for a in shux]# shux2 = np.array(shux1)arr1 = np.zeros((32,32))for index1,a in enumerate(file_content):# print(index1)arr1[index1] = np.array(list(map(int,a)),dtype=np.int8) # 32*32arr1_ravel = arr1.ravel() # 1*1024print(arr1_ravel)arr[index,:-1] = arr1_ravelarr[index,-1] = biaoqianname = dirth.split('\\')[-1]np.savetxt(f'{name}.csv',arr,fmt='%d')except:passif __name__ == '__main__':dirth1 = 'trainingDigits'dirth2 = r'C:\Users\Administrator\Desktop\testDigits'data_train(dirth1)data_train(dirth2)
上面的程序将两个文件夹中的数据进行形式统一,且各自分好了属于每组数的标签,然后保存到两个文件中,接下来需要将测试集中的数据根据训练集种的数据分类来进行KNN算法分类。并最值终确定k值
import pandas as pdimport numpy as np# KNN算法def knn(arr_test,arr_train,k):true_num = 1for i in range(arr_test.shape[0]):test = arr_test[i,:-1]# 求相似度d = np.sqrt(((test - arr_train[:,:-1])**2).sum(axis=1))# 排序sort_index = d.argsort()[:k]tag = arr_train[sort_index,-1]df = pd.DataFrame(tag).mode()print('预测值',df[0][0])print('实际值',arr_test[i,-1])if df[0][0] == arr_test[i,-1]:true_num += 1print('准确度为',true_num/arr_test.shape[0])return true_num/arr_test.shape[0]if __name__ == '__main__':arr_test = np.loadtxt('testDigits.csv', dtype=int)arr_train = np.loadtxt('trainingDigits.csv', dtype=int)y = []for k in range(5,15):prec = knn(arr_test,arr_train,k)y.append(prec)x = range(5,15)import matplotlib.pyplot as pltplt.figure()plt.plot(x,y,marker='*',markersize=12)plt.xlabel('k')plt.ylabel('准确度')plt.show()
最终的折线图如图所示:
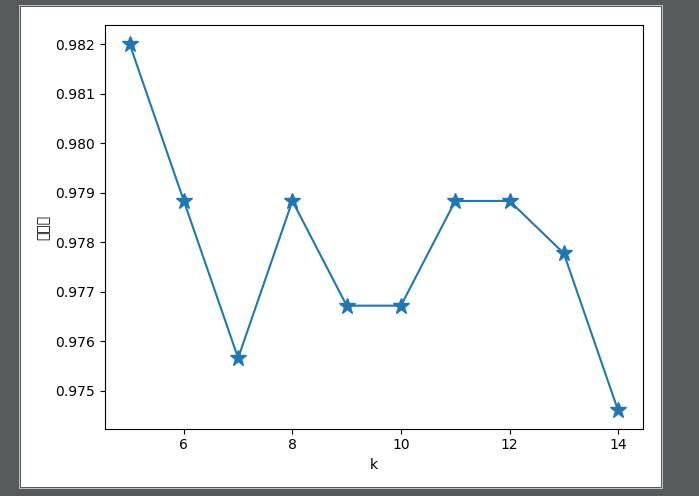
如图所示共选取了十组k值进行最终的准确率比对,发现当k=5的时候准确率最高,说明k=5
产生误差数据的饼图
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltdef knn(test_arr,train_arr,k):test_list = []for i in range(test_arr.shape[0]):test_data = test_arr[i,:-1]# 相似度d = np.sqrt(((test_data - train_arr[:,:-1])**2).sum(axis=1))# 排序sort_index = d.argsort()[:k]tag = train_arr[sort_index,-1]df = pd.DataFrame(tag).mode()value_yuce = df[0][0]value_shiji = test_arr[i,-1]print('预测值',value_yuce)print('实际值',value_shiji)if value_shiji != value_yuce:test_list.append(value_shiji)return test_listif __name__ == '__main__':test_arr = np.loadtxt('testDigits.csv',dtype=int)train_arr = np.loadtxt('trainingDigits.csv',dtype=int)k = 5test_list = knn(test_arr,train_arr,5)print(test_list)data = pd.DataFrame(test_list)data1 = data[0].value_counts()label = data1.indexexplode = [0.01,0.01,0.01,0.01,0.01,0.01]plt.figure()plt.pie(data1,explode=explode,labels=label,autopct='%1.1f%%')plt.savefig('误差数据饼图')plt.show()
图像如图所示:
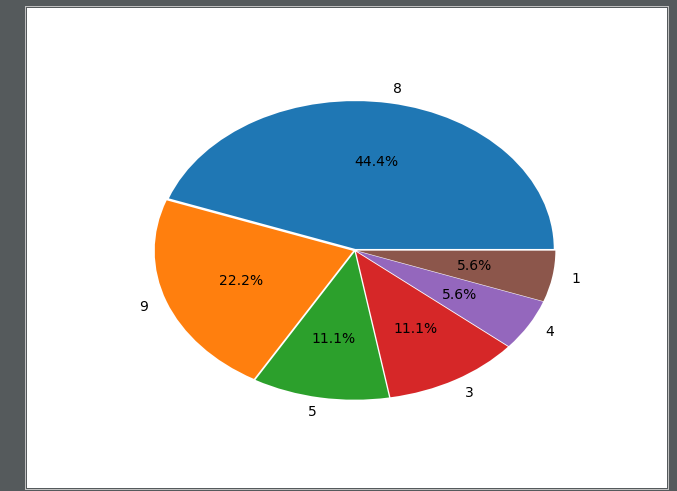
根据上图所示标签为8的数据产生的误差率最大。





























还没有评论,来说两句吧...