机器学习—降维

短命女 2022-02-05 01:13 509阅读 0赞

降维的作用：压缩和可视化

数据压缩（3D–>2D）：减少数据从3D到2D

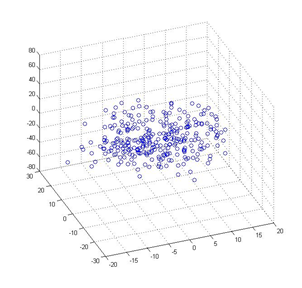
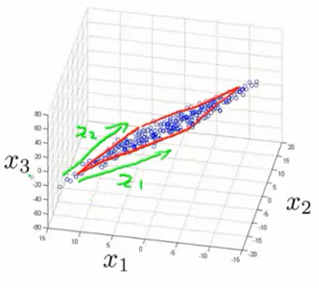
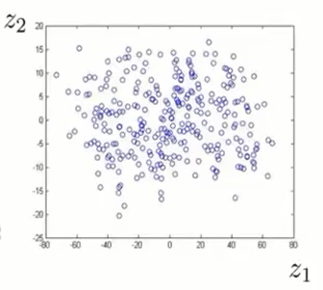
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

可视化数据

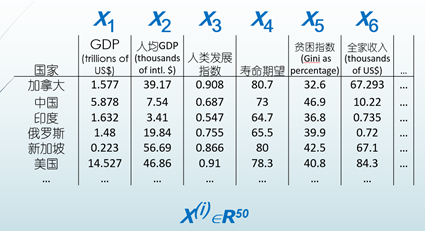
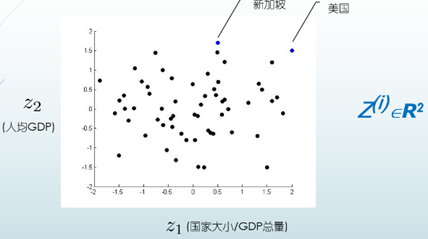
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

主成分分析（PCA）

  • 主成分分析（PCA）是最常见的降维算法。
  • 在PCA中，要做的是找到一个方向向量（Vector direction），当把所有的数据都投射到该向量上时，希望投射距离均方差能尽可能地小。
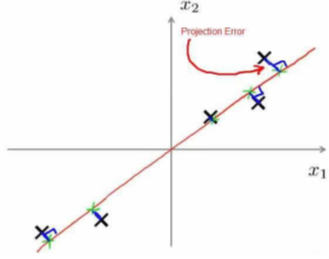
  • 方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。
  • 主成分分析最小化的是投射距离误差（Projected Error）
    在这里插入图片描述

降维算法的几何图形直观理解:

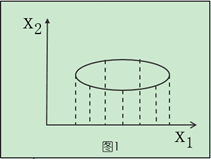
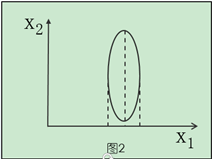
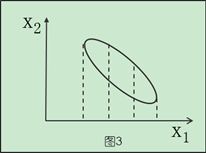
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
将点投影到X1这个维度上看的话，图1的数据离散性最高，图3较低，图2数据离散性是最低的。数据离散性越大，代表数据在所投影的维度上具有越高的区分度，这个区分度就是信息量。如果用方差来形容数据的分布离散性的话，就是向X1轴的投射距离方差越小，在X1方向上投射形成的数据方差则越大，表示数据的区分度越高，也就是蕴含的信息量是越大的。

基于这个知识，如果想对数据进行降维的话，比如图1的两个维度的数据降成一维，可以选择保留X1这个维度的数据(也就是向X1轴的投射距离方差最小)，因为在这个维度上蕴含的信息量更多。

主成分分析问题

  • PCA将n个特征降维到k个，可用来进行数据压缩。
     如果100维的向量最后可以用10维来表示，那么压缩率为90%。
     同样图像处理领域的KL变换使用PCA 做图像压缩。
     但PCA 要保证降维后，还要保证数据的特性损失最小。
     PCA 技术的一大好处是对数据进行降维的处理。
  • 对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。
     同时最大程度的保持了原有数据的信息
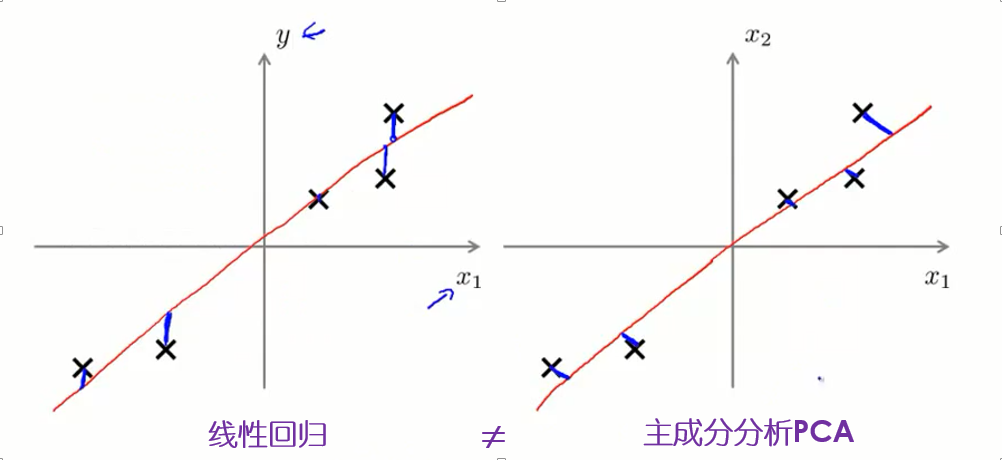
主成分分析的投射距离误差与线性回归的预测误差

主成分分析的投射距离误差与线性回归的预测误差

PCA步骤

1)计算协方差矩阵
2)通过SVD求解特征向量和特征值,使其满足AU=SU ,S为特征值，U是特征向量。将原A变为除方差位置外（对角线），协方差位置都为0的矩阵。
3)选取前k个特征值较大的特征向量做数据压缩Z=XUreduc(k)

注意：在PCA之前要做特征缩放

在这里插入图片描述

协方差矩阵含义

  • 两个特征相交处的值为正，表明两个特征正相关；
  • 值为负，两个特征负相关；
  • 值为0，两个特征不相关。

降维算法的几何图形的数学理解:

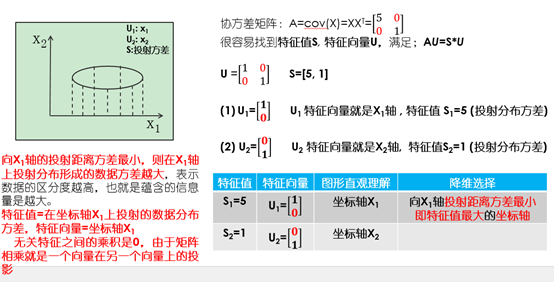
在这里插入图片描述

降维算法的几何图形的数学理解:

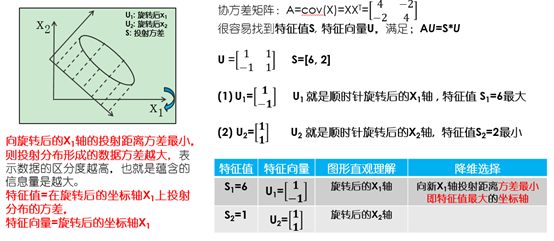
在这里插入图片描述

应用PCA的建议

1.压缩
减少内存及磁盘的数据需求
加速学习算法
可视化

2.PCA的不良应用: 防止过拟合（首选是正则化）
这不是一个处理过度拟合的好方法，因为其降维时与结果无关，所以可能会将一些与结果有关的特征丢失. 需要使用正则化代替.（与结果有关）

3.在实现PCA之前,首先尝试用原始/原始数据 来运行任何你想做的事情.只有必要时（算法运行太慢或者占用太多
内存）, 才考虑使用PCA.

发表评论

表情：
评论列表 （有 0 条评论，509人围观）

还没有评论，来说两句吧...

相关阅读

    相关 机器学习-PCA降维

    PCA(Principal Component Analysis 主成分分析) PCA主要用于非线性数据的降维，需要用到核技巧。因此在使用的时候需要选择合适的核函数并对核函

    快来打我*快来打我*/ 0 赞/ 416 阅读

    相关 机器学习算法08 - 降维学习

    降维学习 在概率统计模块，我详细讲解了如何使用各种统计指标来进行特征的选择，降低用于监督式学习的特征之维度。接下来的几节，我会阐述两种针对数值型特征，更为通用的降维方法，

    冷不防冷不防/ 0 赞/ 428 阅读