人脸损失函数的各种变体

柔情只为你懂 2022-02-15 18:17 218阅读 0赞

人脸损失函数的各种变体都是基于softmax的交叉熵损失函数进行改进的，因此本文首先介绍基础形式，然后对各种变体进行说明。

*  基于softmax的交叉熵损失函数

先放上两者的基本形式

![E(x)=-\\sum p\{\_\{x\}\}\*log(q\{\_\{x\}\})][E_x_-_sum p_x_log_q_x]   CE形式，其中![p\{\_\{x\}\}][p_x]为样本真实分布，![q\{\_\{x\}\}][q_x]为该样本观察分布

![\\sigma (z\_\{j\})=\\frac\{e^\{z\{\_\{j\}\}\}\}\{\\sum\_\{k=1\}^\{K\}\{e^\{z\{\_\{k\}\}\}\}\}][sigma _z_j_frac_e_z_j_sum_k_1_K_e_z_k]                  Softmax形式

基于softmax的交叉熵损失函数，就是利用softmax的值替代CE中样本的观察分布![q\{\_\{x\}\}][q_x]，真实分布![p\{\_\{x\}\}][p_x]为one-hot向量。具体计算过程可参考tf[损失函数][Link 1]的参数，其中labels传入样本真实分布，logits值传入softmax计算所需要的![z\{\_\{k\}\}][z_k]值。

*  人脸其他损失函数变体的由来

针对上述基本形式，真实分布的one-hot向量不会改变，指数和对数计算函数不改变的情况下，影响计算结果的只有标量![z\{\_\{j\}\}][z_j]的值。而![z\{\_\{j\}\}][z_j]是通过![w\{\_\{j\}\}\*x\{\_\{j\}\}+b\{\_\{j\}\}][w_j_x_j_b_j]计算获得的，因此针对向量点乘的公式被拔得体无完肤。总的来说都是利用余弦函数在\[0,![\\pi][pi]\]区间单调递减的特性来达到目标的。

*  [L-Softmax Loss][]和[A-Softmax][](SphereFace)

![L\{\_\{i\}\}=-log(\\frac\{e^\{\\left \\| w\{\_\{y\{\_\{i\}\}\}\} \\right \\|\\left \\| x\{\_\{i\}\} \\right \\|\\psi (\\theta y\{\_\{i\}\})\}\}\{e^\{\\left \\| w\{\_\{y\{\_\{i\}\}\}\} \\right \\|\\left \\| x\{\_\{i\}\} \\right \\|\\psi (\\theta y\{\_\{i\}\})\}+\\sum \{\_\{j\\neq y\{\_\{i\}\}\}\}e^\{\\left \\| w\{\_\{y\{\_\{i\}\}\}\} \\right \\|\\left \\| x\{\_\{i\}\} \\right \\|\\cos(\\theta\{\_\{j\}\})\}\})][L_i_-log_frac_e_left _ w_y_i_ _right _left _ x_i_ _right _psi _theta y_i_e_left _ w_y_i_ _right _left _ x_i_ _right _psi _theta y_i_sum _j_neq y_i_e_left _ w_y_i_ _right _left _ x_i_ _right _cos_theta_j]      其中![\\psi (\\theta )=\\left\\\{\\begin\{matrix\} cos(m\\theta ), 0\\leqslant \\theta \\leqslant \\frac\{\\pi \}\{m\} & \\\\ D(\\theta ), \\frac\{\\pi \}\{m\}< \\theta \\leqslant \\pi & \\end\{matrix\}\\right.][psi _theta _left_begin_matrix_ cos_m_theta _ 0_leqslant _theta _leqslant _frac_pi _m_ _ _ D_theta _ _frac_pi _m_ _theta _leqslant _pi _ _end_matrix_right.]       L-Softmax形式

![L\{\_\{ang\}\}=\\frac\{1\}\{N\}\\sum\_\{i\}-log(\\frac\{e^\{\{\\left \\| x\{\_\{i\}\} \\right \\|\}\\psi (\\theta \{\_\{y\{\_\{i\}\}\}\},\{\_\{i\}\})\}\}\{e^\{\{\\left \\| x\{\_\{i\}\} \\right \\|\}\\psi (\\theta \{\_\{y\{\_\{i\}\}\}\},\{\_\{i\}\})\}+\\sum \{\_\{j\\neq y\{\_\{i\}\}\}\}e^\{\{\\left \\| x\{\_\{i\}\} \\right \\|\}cos (\\theta \{\_\{j\}\},\{\_\{i\}\})\}\})][L_ang_frac_1_N_sum_i_-log_frac_e_left _ x_i_ _right _psi _theta _y_i_i_e_left _ x_i_ _right _psi _theta _y_i_i_sum _j_neq y_i_e_left _ x_i_ _right _cos _theta _j_i]      其中![\\psi (\\theta \{y\{\_\{i\}\},i\})=(-1)^\{k\}cos(m\\theta\{y\{\_\{i\}\}\},\{\_\{i\}) -2k][psi _theta _y_i_i_-1_k_cos_m_theta_y_i_i_ -2k] ![gif.latex][] A-Softmax形式

上述两个损失函数主要是针对向量夹角进行的改进，即样本与对应权重间的夹角由![\\theta][theta]变为![m\\theta][m_theta]，由于当m>1时，![cos(\\theta )>cos(m\\theta )][cos_theta _cos_m_theta]，这样以来当样本与权重在较大夹角情况下满足点乘值最大时，类别的泛化能力更好，另一方面使得类内间距更小，类间间距更大。

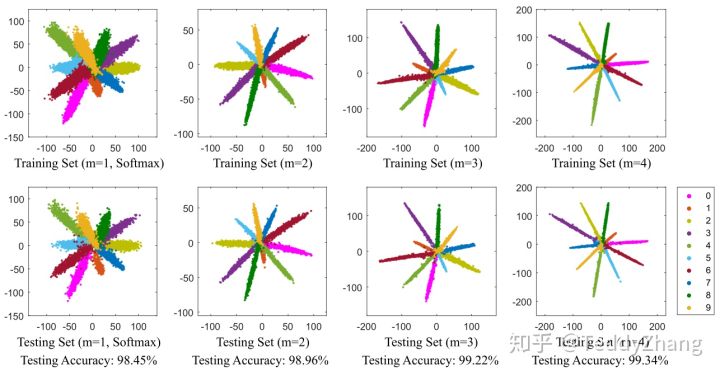![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2h6aGoyMDA3_size_16_color_FFFFFF_t_70][] 分别基于Softmax和L-Softmax训练后网络特征的可视化

*  LMCL（[Large Margin Cosine Loss, CosFace][Large Margin Cosine Loss_ CosFace]）和[AM-Softmax Loss][]

![L\{\_\{lmc\}\}=\\frac\{1\}\{N\}\\sum\_\{i\}-log\\frac\{e^\{s(cos(\\theta \{\_\{y\{\_\{i\}\}\},\_\{i\}\})-m)\}\}\{e^\{s(cos(\\theta \{\_\{y\{\_\{i\}\}\},\_\{i\}\})-m) + \\sum \{\_\{j \\neq y\{\_\{i\}\} \}e^\{scos(\\theta \{\_\{j,i\}\})\}\}\}\}][L_lmc_frac_1_N_sum_i_-log_frac_e_s_cos_theta _y_i_i_-m_e_s_cos_theta _y_i_i_-m_ _ _sum _j _neq y_i_ _e_scos_theta _j_i]        CosFace损失函数，![m\\in \[0, \\frac\{c\}\{c-1\})][m_in _0_ _frac_c_c-1]

![L\{\_\{AMS\}\}=-\\frac\{1\}\{n\}\\sum\_\{i=1\}^\{n\}log\\frac\{e^\{s\\cdot (cos\\theta \{\_\{y\{\_\{i\}\}\}-m\})\}\}\{e^\{s\\cdot (cos\\theta \{\_\{y\{\_\{i\}\}\}-m\})\}+\\sum \_\{j=1,j\\neq y\{\_\{i\}\}\}^\{C\}e^\{s\\cdot cos\\theta\{\_\{j\}\}\}\}][L_AMS_-_frac_1_n_sum_i_1_n_log_frac_e_s_cdot _cos_theta _y_i_-m_e_s_cdot _cos_theta _y_i_-m_sum _j_1_j_neq y_i_C_e_s_cdot cos_theta_j]         AM-Softmax 损失函数

两篇论文的损失函数都是通过对余弦距离的结果进行的改进，即在原来余弦距离的基础上增加m的冗余。针对余弦距离的修改比针对角度距离的修改后分类效果更佳明显。至于s的由来，可参考论文CosFace中的说法：![\\left \\| x \\right \\|][left _ x _right]对得分函数没有贡献，因此将该值使用s进行替代。

*  [ArcFace][]

![L=-\\frac\{1\}\{N\}\\sum\_\{i=1\}^\{N\}log\\frac\{e\{^\{s(cos(\\theta y\{\_\{i\}\} + m))\}\}\}\{e\{^\{s(cos(\\theta y\{\_\{i\}\} + m))\}\} + \\sum\{^\{n\}\}\{\_\{j=1,j\\neq y\{\_\{i\}\}\}\}e\{^\{scos\\theta\{\_\{j\}\}\}\}\}][L_-_frac_1_N_sum_i_1_N_log_frac_e_s_cos_theta y_i_ _ m_e_s_cos_theta y_i_ _ m_ _ _sum_n_j_1_j_neq y_i_e_scos_theta_j]   ArcFace的损失函数

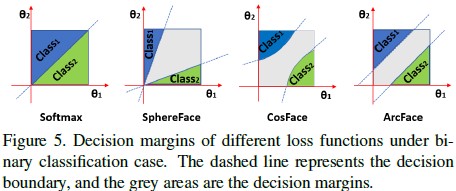
论文对向量夹角进行的改进，不同于L-Softmax和A-Softmax成倍增加夹角的是该损失函数在原夹角基础上增加m的冗余。下图直观的反映了不同损失函数的夹角对决策面的影响。

![20190426154604251.jpg][]

参考文献：

1.  [人脸识别：损失函数总结][Link 2]
2.  [人脸识别损失函数简介与Pytorch实现：ArcFace、SphereFace、CosFace][Pytorch_ArcFace_SphereFace_CosFace]

[E_x_-_sum p_x_log_q_x]: https://private.codecogs.com/gif.latex?E%28x%29%3D-%5Csum%20p%7B_%7Bx%7D%7D*log%28q%7B_%7Bx%7D%7D%29
[p_x]: https://private.codecogs.com/gif.latex?p%7B_%7Bx%7D%7D
[q_x]: https://private.codecogs.com/gif.latex?q%7B_%7Bx%7D%7D
[sigma _z_j_frac_e_z_j_sum_k_1_K_e_z_k]: https://private.codecogs.com/gif.latex?%5Csigma%20%28z_%7Bj%7D%29%3D%5Cfrac%7Be%5E%7Bz%7B_%7Bj%7D%7D%7D%7D%7B%5Csum_%7Bk%3D1%7D%5E%7BK%7D%7Be%5E%7Bz%7B_%7Bk%7D%7D%7D%7D%7D
[Link 1]: https://www.w3cschool.cn/tensorflow_python/tf_nn_sparse_softmax_cross_entropy_with_logits.html
[z_k]: https://private.codecogs.com/gif.latex?z%7B_%7Bk%7D%7D
[z_j]: https://private.codecogs.com/gif.latex?z%7B_%7Bj%7D%7D
[w_j_x_j_b_j]: https://private.codecogs.com/gif.latex?w%7B_%7Bj%7D%7D*x%7B_%7Bj%7D%7D&plus;b%7B_%7Bj%7D%7D
[pi]: https://private.codecogs.com/gif.latex?%5Cpi
[L-Softmax Loss]: http://proceedings.mlr.press/v48/liud16.pdf
[A-Softmax]: https://arxiv.org/pdf/1704.08063.pdf
[L_i_-log_frac_e_left _ w_y_i_ _right _left _ x_i_ _right _psi _theta y_i_e_left _ w_y_i_ _right _left _ x_i_ _right _psi _theta y_i_sum _j_neq y_i_e_left _ w_y_i_ _right _left _ x_i_ _right _cos_theta_j]: https://private.codecogs.com/gif.latex?L%7B_%7Bi%7D%7D%3D-log%28%5Cfrac%7Be%5E%7B%5Cleft%20%5C%7C%20w%7B_%7By%7B_%7Bi%7D%7D%7D%7D%20%5Cright%20%5C%7C%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%5Cpsi%20%28%5Ctheta%20y%7B_%7Bi%7D%7D%29%7D%7D%7Be%5E%7B%5Cleft%20%5C%7C%20w%7B_%7By%7B_%7Bi%7D%7D%7D%7D%20%5Cright%20%5C%7C%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%5Cpsi%20%28%5Ctheta%20y%7B_%7Bi%7D%7D%29%7D&plus;%5Csum%20%7B_%7Bj%5Cneq%20y%7B_%7Bi%7D%7D%7D%7De%5E%7B%5Cleft%20%5C%7C%20w%7B_%7By%7B_%7Bi%7D%7D%7D%7D%20%5Cright%20%5C%7C%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%5Ccos%28%5Ctheta%7B_%7Bj%7D%7D%29%7D%7D%29
[psi _theta _left_begin_matrix_ cos_m_theta _ 0_leqslant _theta _leqslant _frac_pi _m_ _ _ D_theta _ _frac_pi _m_ _theta _leqslant _pi _ _end_matrix_right.]: https://private.codecogs.com/gif.latex?%5Cpsi%20%28%5Ctheta%20%29%3D%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20cos%28m%5Ctheta%20%29%2C%200%5Cleqslant%20%5Ctheta%20%5Cleqslant%20%5Cfrac%7B%5Cpi%20%7D%7Bm%7D%20%26%20%5C%5C%20D%28%5Ctheta%20%29%2C%20%5Cfrac%7B%5Cpi%20%7D%7Bm%7D%3C%20%5Ctheta%20%5Cleqslant%20%5Cpi%20%26%20%5Cend%7Bmatrix%7D%5Cright.
[L_ang_frac_1_N_sum_i_-log_frac_e_left _ x_i_ _right _psi _theta _y_i_i_e_left _ x_i_ _right _psi _theta _y_i_i_sum _j_neq y_i_e_left _ x_i_ _right _cos _theta _j_i]: https://private.codecogs.com/gif.latex?L%7B_%7Bang%7D%7D%3D%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%7D-log%28%5Cfrac%7Be%5E%7B%7B%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%7D%5Cpsi%20%28%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D%7D%2C%7B_%7Bi%7D%7D%29%7D%7D%7Be%5E%7B%7B%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%7D%5Cpsi%20%28%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D%7D%2C%7B_%7Bi%7D%7D%29%7D&plus;%5Csum%20%7B_%7Bj%5Cneq%20y%7B_%7Bi%7D%7D%7D%7De%5E%7B%7B%5Cleft%20%5C%7C%20x%7B_%7Bi%7D%7D%20%5Cright%20%5C%7C%7Dcos%20%28%5Ctheta%20%7B_%7Bj%7D%7D%2C%7B_%7Bi%7D%7D%29%7D%7D%29
[psi _theta _y_i_i_-1_k_cos_m_theta_y_i_i_ -2k]: https://private.codecogs.com/gif.latex?%5Cpsi%20%28%5Ctheta%20%7By%7B_%7Bi%7D%7D%2Ci%7D%29%3D%28-1%29%5E%7Bk%7Dcos%28m%5Ctheta%7By%7B_%7Bi%7D%7D%7D%2C%7B_%7Bi%7D%29%20-2k
[gif.latex]: https://private.codecogs.com/gif.latex?
[theta]: https://private.codecogs.com/gif.latex?%5Ctheta
[m_theta]: https://private.codecogs.com/gif.latex?m%5Ctheta
[cos_theta _cos_m_theta]: https://private.codecogs.com/gif.latex?cos%28%5Ctheta%20%29%3Ecos%28m%5Ctheta%20%29
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2h6aGoyMDA3_size_16_color_FFFFFF_t_70]: /images/20220215/17e86b873d334963b4f607a7a8f5296e.png
[Large Margin Cosine Loss_ CosFace]: https://arxiv.org/pdf/1801.09414.pdf
[AM-Softmax Loss]: https://arxiv.org/pdf/1801.05599.pdf
[L_lmc_frac_1_N_sum_i_-log_frac_e_s_cos_theta _y_i_i_-m_e_s_cos_theta _y_i_i_-m_ _ _sum _j _neq y_i_ _e_scos_theta _j_i]: https://private.codecogs.com/gif.latex?L%7B_%7Blmc%7D%7D%3D%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%7D-log%5Cfrac%7Be%5E%7Bs%28cos%28%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D%2C_%7Bi%7D%7D%29-m%29%7D%7D%7Be%5E%7Bs%28cos%28%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D%2C_%7Bi%7D%7D%29-m%29%20&plus;%20%5Csum%20%7B_%7Bj%20%5Cneq%20y%7B_%7Bi%7D%7D%20%7De%5E%7Bscos%28%5Ctheta%20%7B_%7Bj%2Ci%7D%7D%29%7D%7D%7D%7D
[m_in _0_ _frac_c_c-1]: https://private.codecogs.com/gif.latex?m%5Cin%20%5B0%2C%20%5Cfrac%7Bc%7D%7Bc-1%7D%29
[L_AMS_-_frac_1_n_sum_i_1_n_log_frac_e_s_cdot _cos_theta _y_i_-m_e_s_cdot _cos_theta _y_i_-m_sum _j_1_j_neq y_i_C_e_s_cdot cos_theta_j]: https://private.codecogs.com/gif.latex?%5Cinline%20L%7B_%7BAMS%7D%7D%3D-%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dlog%5Cfrac%7Be%5E%7Bs%5Ccdot%20%28cos%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D-m%7D%29%7D%7D%7Be%5E%7Bs%5Ccdot%20%28cos%5Ctheta%20%7B_%7By%7B_%7Bi%7D%7D%7D-m%7D%29%7D&plus;%5Csum%20_%7Bj%3D1%2Cj%5Cneq%20y%7B_%7Bi%7D%7D%7D%5E%7BC%7De%5E%7Bs%5Ccdot%20cos%5Ctheta%7B_%7Bj%7D%7D%7D%7D
[left _ x _right]: https://private.codecogs.com/gif.latex?%5Cleft%20%5C%7C%20x%20%5Cright%20%5C%7C
[ArcFace]: https://arxiv.org/abs/1801.07698
[L_-_frac_1_N_sum_i_1_N_log_frac_e_s_cos_theta y_i_ _ m_e_s_cos_theta y_i_ _ m_ _ _sum_n_j_1_j_neq y_i_e_scos_theta_j]: https://private.codecogs.com/gif.latex?L%3D-%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7Dlog%5Cfrac%7Be%7B%5E%7Bs%28cos%28%5Ctheta%20y%7B_%7Bi%7D%7D%20&plus;%20m%29%29%7D%7D%7D%7Be%7B%5E%7Bs%28cos%28%5Ctheta%20y%7B_%7Bi%7D%7D%20&plus;%20m%29%29%7D%7D%20&plus;%20%5Csum%7B%5E%7Bn%7D%7D%7B_%7Bj%3D1%2Cj%5Cneq%20y%7B_%7Bi%7D%7D%7D%7De%7B%5E%7Bscos%5Ctheta%7B_%7Bj%7D%7D%7D%7D%7D
[20190426154604251.jpg]: /images/20220215/58bff34f8cda487094830c20e8ed644d.png
[Link 2]: https://zhuanlan.zhihu.com/p/59440497
[Pytorch_ArcFace_SphereFace_CosFace]: https://zhuanlan.zhihu.com/p/60747096