算法之暴力破解法(穷举法)
一,什么是暴力破解法?
暴力破解法,就是把所有条件,相关情况统统考虑进去,让计算机进行检索,指导得出与之所有条件符合的结果
(但是,暴力破解法对计算机资源耗费严重,如果条件太复杂,运算速度缓慢,为了解决这一问题,我们可以事先把与之不相关的条件进行限制,减少计算机的运算量)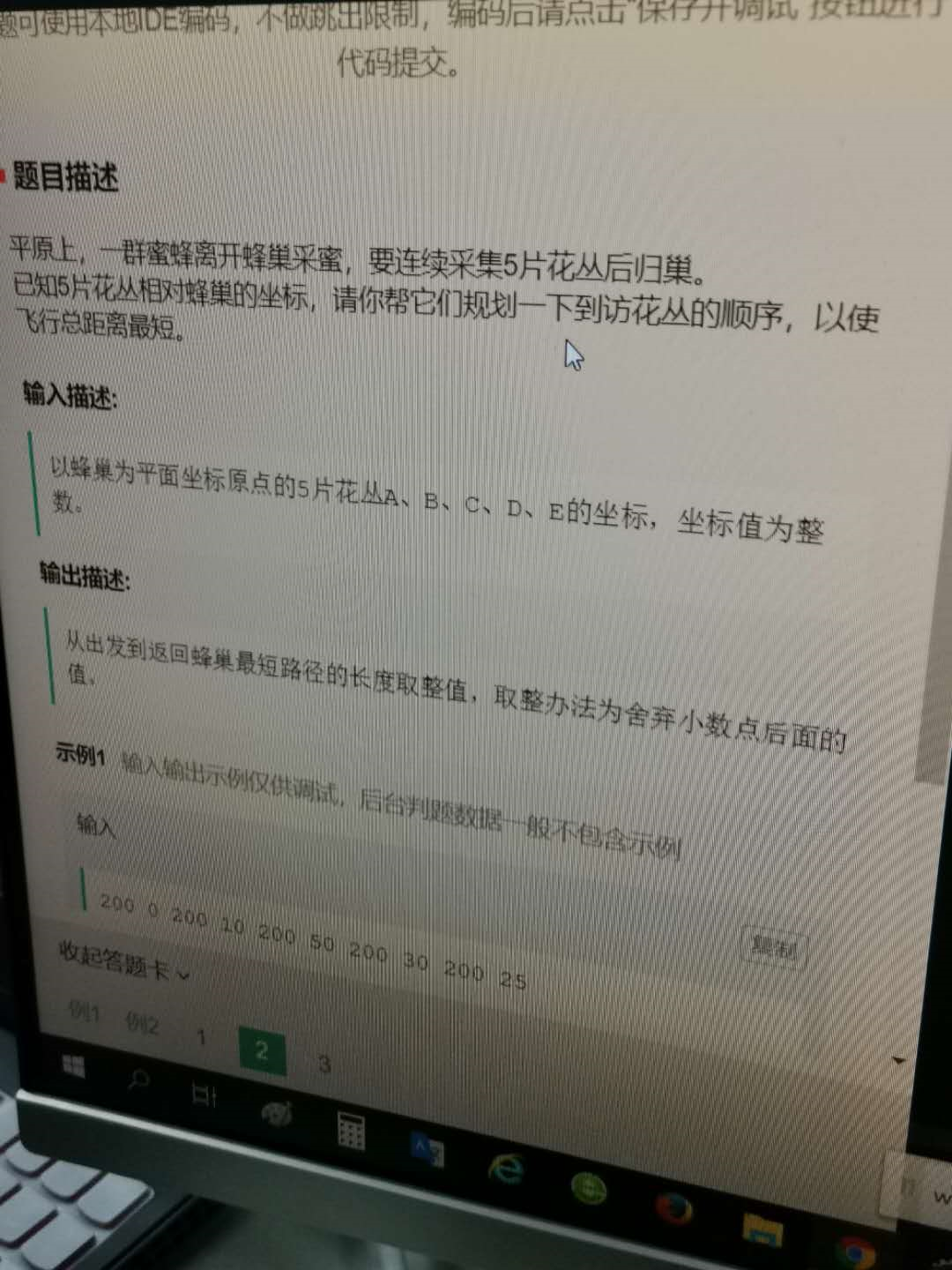
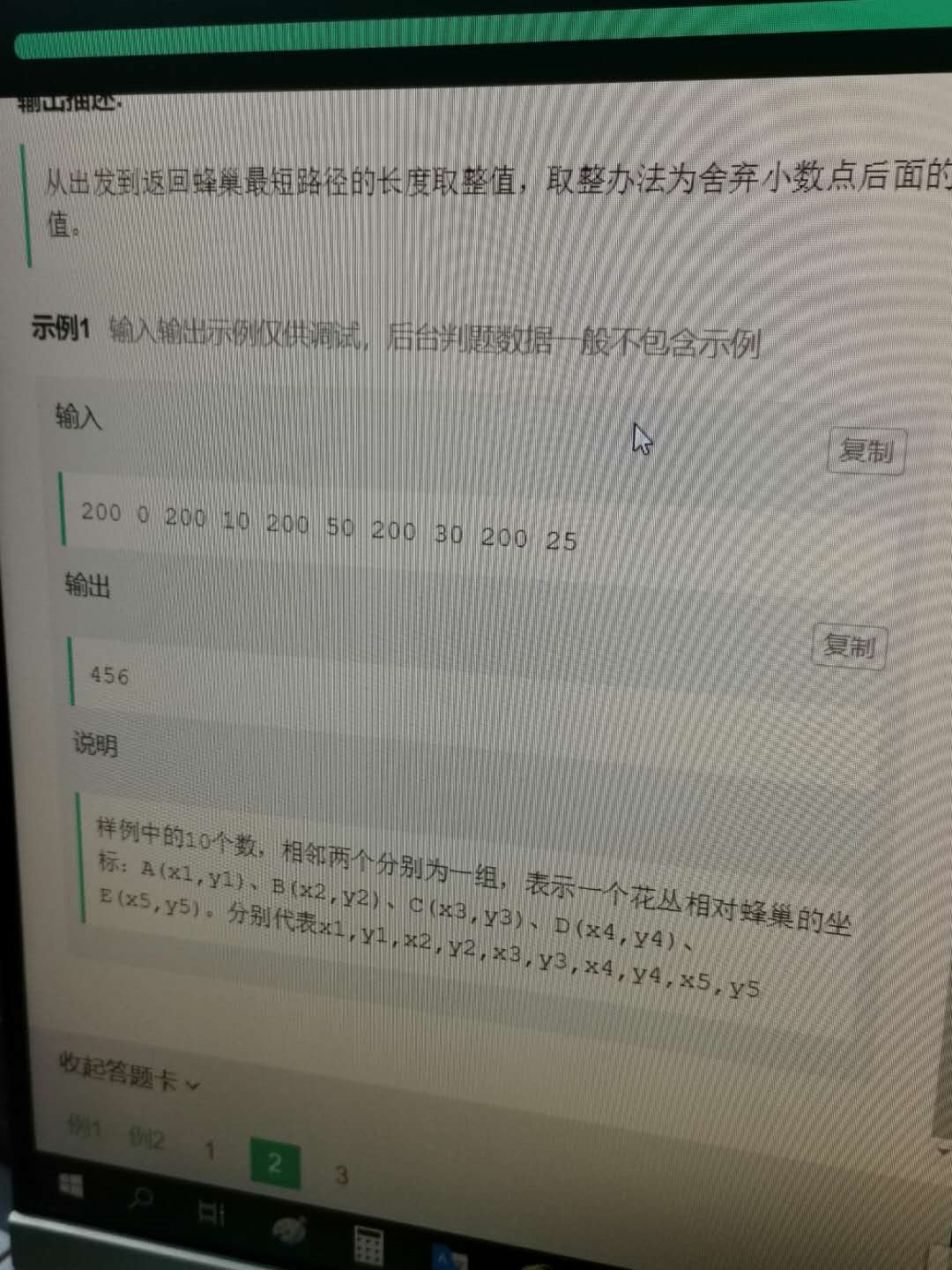
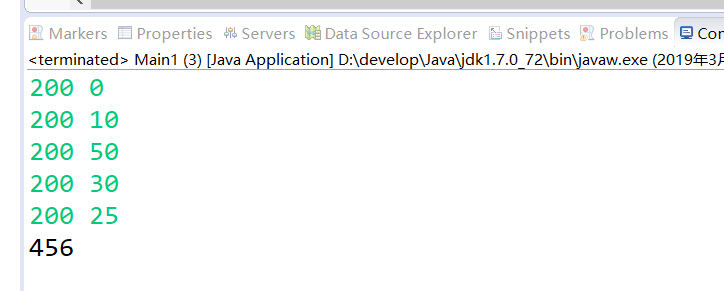
把所有情况都给列出来了,蜜蜂每次到的点都有五种可能性,先确定了第一次跑的一种可能性,是第一个点,那么第二个点就不能出现第一个点,但是其他点可以,在确定第三个点时,要排除前两个走过的点,依次类推,到最后一个只能是剩下来的那个点,并计算其中每段距离,在累和起来就是这一条路径的总距离,再把这个总距离作为一个元素存到一个动态数组;最后这样的方式来五回,把所有可能列出来,计算所有路径的长度,都存放到动态数组中,最后再来一步,看看数组中谁最小就好
package com.test3;import java.util.ArrayList;import java.util.Collections;import java.util.Scanner;public class Main1 {public static void main(String[] args) {/** 集合ArrayList,存储int类型数* 集合本身不接受基本类型,自动装箱存储*/Scanner sc = new Scanner(System.in);ArrayList<int[]> list = new ArrayList<int[]>();//将所有坐标存入数组中for (int i = 0; i < 5; i++) {int[] arraytemp = new int[2];for (int j = 0; j < 2; j++) {arraytemp[j] = sc.nextInt();}//将每对坐标存入ArrayListlist.add(arraytemp);}//每段距离的存储变量double ln1 = 0;double ln2 = 0;double ln3 = 0;double ln4 = 0;double ln5 = 0;double ln6 = 0;double sum = 0;//存储每一条路径的总距离ArrayList<Double> listSum = new ArrayList<Double>();//暴力检索for (int i = 0; i < 5; i++) {//求出第一段距离ln1 = Math.sqrt(Math.pow(list.get(i)[0], 2) + Math.pow(list.get(i)[1], 2));//求第二段距离for (int i1 = 0; i1 < 5; i1++) {//排除与之重复的坐标if (list.get(i1) == list.get(i)) {continue;}else{ln2 = Math.sqrt(Math.pow(list.get(i1)[0]-list.get(i)[0], 2) + Math.pow(list.get(i1)[1]-list.get(i)[1], 2));}//求第三段距离for (int i2 = 0; i2 < 5; i2++) {//排除与之重复的坐标if(list.get(i2) == list.get(i1) || list.get(i2) == list.get(i)){continue;}else{ln3 = Math.sqrt(Math.pow(list.get(i2)[0]-list.get(i1)[0], 2) + Math.pow(list.get(i2)[1]-list.get(i1)[1], 2));}//第四段距离for (int i3 = 0; i3 < 5; i3++) {//排除与之重复的坐标if(list.get(i3) == list.get(i2)||list.get(i3) == list.get(i1) || list.get(i3) == list.get(i)){continue;}else{ln4 = Math.sqrt(Math.pow(list.get(i3)[0]-list.get(i2)[0], 2) + Math.pow(list.get(i3)[1]-list.get(i2)[1], 2));}//第五段距离for (int i4 = 0; i4 < 5; i4++) {//排除与之重复的坐标if(list.get(i4) == list.get(i3)||list.get(i4) == list.get(i2)||list.get(i4) == list.get(i1) || list.get(i4) == list.get(i)){continue;}else{ln5 = Math.sqrt(Math.pow(list.get(i4)[0]-list.get(i3)[0], 2) + Math.pow(list.get(i4)[1]-list.get(i3)[1], 2));}//第六段距离ln6 = Math.sqrt(Math.pow(list.get(i4)[0], 2) + Math.pow(list.get(i4)[1], 2));sum = ln1 + ln2 + ln3 + ln4 + ln5 + ln6;listSum.add(sum);}}}}}Collections.sort(listSum);double num;num = listSum.get(0);int result = (int) num;System.out.println(result);}}

































还没有评论,来说两句吧...