1. ICP算法

2D-2D问题是通过已知的2D图像坐标点对来求解图像间的变换关系（即 R R R 和 t t t）。3D-2D问题是通过已知的3D空间点坐标和对应的2D像素坐标来求解图像的位姿。所以很显然，3D-3D问题是根据已知的3D空间点对来求解图像图像间的变换关系。

假设我们有一组配对好的 3D 点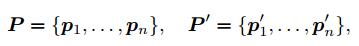
在这里插入图片描述
现在想要找到一个欧式变换 R R R， t t t，使得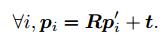

这个问题可以用迭代最近点（Iterative Closest Point, ICP）求解。可以看到3D-3D 位姿估计问题中，并没有出现相机模型，也就是说，仅考虑两组 3D 点之间的变换时，和相机并没有关系。因此，在激光 SLAM 中也会碰到 ICP，不过由于激光数据特征不够丰富，我们无从知道两个点集之间的匹配关系，只能认为距离最近的两个点为同一个，所以这个方法称为迭代最近点。而在视觉中，特征点为我们提供了较好的匹配关系，所以整个问题就变得更简单了。在 RGB-D SLAM 中，可以用这种方式估计相机位姿。下文我们用 ICP 指代匹配好的两组点间运动估计问题。

和 PnP 类似， ICP 的求解也分为两种方式：利用线性代数的求解（主要是 SVD），以及利用非线性优化方式的求解（类似于 Bundle Adjustment）。下面分别来介绍它们。

2. SVD方法

根据前面描述的 ICP 问题，我们定义第 i i i 对点的误差项： e i = p i − ( R p i ’ + t ) e_i=p_i-(Rp_i^’ + t) ei=pi−(Rpi’+t) 构建最小二乘问题，求使误差平方和达到极小的 R R R 和 t t t ：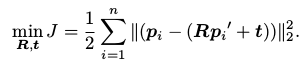
在这里插入图片描述
接下来，来推导它的求解方法。

首先,定义两组点的质心: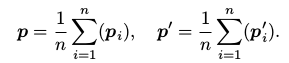
在这里插入图片描述
随后,在误差函数中,我们作如下的处理: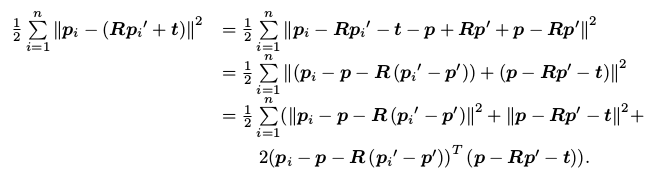

注意到交叉项部分中， ( p i − p − R ( p i ′ − p ′ ) ) (p_i − p − R (p_i^′ − p^′ )) (pi−p−R(pi′−p′))在求和之后是为零的，因此优化目标函数可以简化为: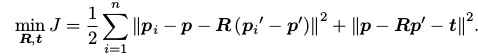

仔细观察左右两项，我们发现左边只和旋转矩阵 R 相关，而右边既有 R 也有 t，但只和质心相关。只要我们获得了 R，令第二项为零就能得到 t。于是，ICP 可以分为以下三个步骤求解:

计算两组点的质心位置 p p p和 p ′ p^′ p′ ，然后计算每个点的去质心坐标： q i = p i − p q_i = p_i-p qi=pi−p q i ′ = p i ′ − p ′ q_i' = p_i'-p' qi′=pi′−p′
根据以下优化问题计算旋转矩阵: R ∗ = a r g m i n 1 2 ∑ i = 1 n ∣ ∣ q i − R q i ′ ∣ ∣ 2 R^* = arg min\frac{1}{2}\sum_{i=1}^{n}\mid\mid{q_i-Rq_i'}\mid\mid^2 R∗=argmin21i=1∑n∣∣qi−Rqi′∣∣2
根据第二步的 R R R，计算 t t t： t ∗ = p − R p ′ t^* = p-Rp' t∗=p−Rp′

我们看到,只要求出了两组点之间的旋转,平移量是非常容易得到的。所以我们重点关注 R 的计算。展开关于 R 的误差项，得: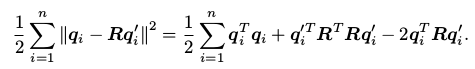
在这里插入图片描述
注意到第一项和 R 无关,第二项由于 R T R = I,亦与 R 无关。因此,实际上优化目标函数变为: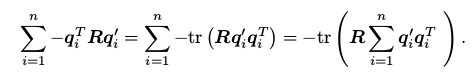

接下来,我们介绍怎样通过 SVD 解出上述问题中最优的 R，为了解 R，先定义矩阵: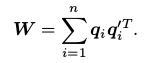

W W W是一个 3 × 3 的矩阵,对 W W W 进行 SVD 分解，得: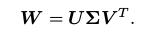
在这里插入图片描述
其中, Σ Σ Σ 为奇异值组成的对角矩阵,对角线元素从大到小排列,而 U U U 和 V V V 为正交矩阵。当 W W W 满秩时, R R R 为: R = U V T R=UV^T R=UVT

解得 R R R 后，便可求出 t t t.

3.非线性优化方法

求解 ICP 的另一种方式是使用非线性优化,以迭代的方式去找最优值。该方法和前面讲述的 PnP 非常相似。以李代数表达位姿时,目标函数可以写成: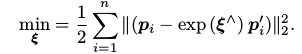
在这里插入图片描述
单个误差项关于位姿导数已经在前面推导过了,使用李代数扰动模型即可: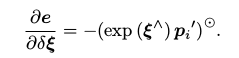

于是，在非线性优化中只需不断迭代，我们就能找到极小值。而且，可以证明， ICP问题存在唯一解或无穷多解的情况。在唯一解的情况下，只要我们能找到极小值解，那么这个极小值就是全局最优值——因此不会遇到局部极小而非全局最小的情况。这也意味着ICP 求解可以任意选定初始值。这是已经匹配点时求解 ICP 的一大好处。

需要说明的是，我们这里讲的 ICP,是指已经由图像特征给定了匹配的情况下，进行位姿估计的问题。在匹配已知的情况下，这个最小二乘问题实际上具有解析解，所以并没有必要进行迭代优化。ICP 的研究者们往往更加关心匹配未知的情况。不过，在RGB-D SLAM 中，由于一个像素的深度数据可能测量不到，所以我们可以混合着使用 PnP和 ICP 优化：对于深度已知的特征点，用建模它们的 3D-3D 误差；对于深度未知的特征点，则建模 3D-2D 的重投影误差。于是，可以将所有的误差放在同一个问题中考虑，使得求解更加方便。