布隆过滤器

系统管理员 2022-03-25 07:37 311阅读 0赞

# 布隆过滤器原理 #

## 布隆过滤器有什么用？ ##

布隆过滤器是可以用于**判断一个元素是不是在一个集合里**，并且相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。

特点：

*  巴顿.布隆于一九七零年提出
 *  一个很长的二进制向量 （位数组）
 *  一系列随机函数 (哈希)
 *  空间效率和查询效率高：O（1）
 *  有一定的误判率（哈希表是精确匹配）

## 实现原理 ##

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m，哈希函数的个数为k

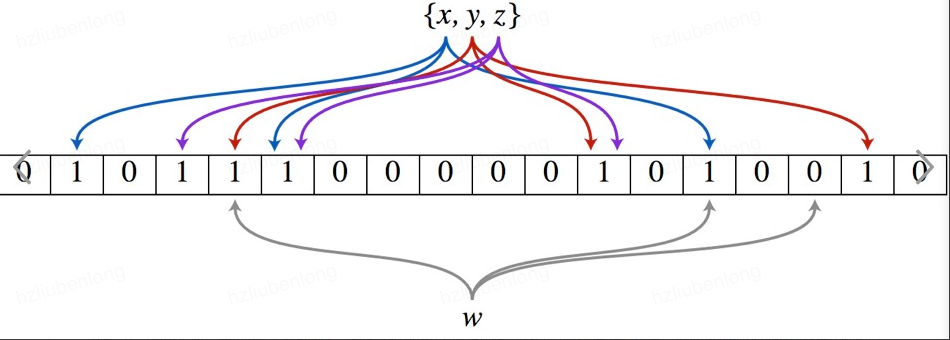
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2ZneWlidXBp_size_16_color_FFFFFF_t_70]  
以上图为例，具体的操作流程：假设集合里面有3个元素\{x, y, z\}，哈希函数的个数为3（这里元素个数和哈希函数的数量没有直接关系）。

首先将位数组进行初始化，将里面每个位都设置位0。

对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，这个值对应位数组上面的一个点，然后将位数组对应的位置标记为1。

查询W元素是否存在集合中的时候，同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1，则可以判断该元素一定不存在集合中。反之，如果3个点都为1，则该元素可能存在集合中。

注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。可以从图中可以看到：假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

## java代码实现 ##

可以看下面这段代码，也可以到 [https://archive.codeplex.com/?p=bloomfilter][https_archive.codeplex.com_p_bloomfilter] 这个地址看开源代码

import java.io.Serializable;
    import java.util.BitSet;
    import java.util.concurrent.atomic.AtomicInteger;
     
    public class BloomFileter implements Serializable { 
        private static final long serialVersionUID = -5221305273707291280L;
        private final int[] seeds;
        private final int size;
        private final BitSet notebook;
        private final MisjudgmentRate rate;
        private final AtomicInteger useCount = new AtomicInteger(0);
        private final Double autoClearRate;
     
        /** * 默认中等程序的误判率：MisjudgmentRate.MIDDLE 以及不自动清空数据（性能会有少许提升） * * @param dataCount 预期处理的数据规模，如预期用于处理1百万数据的查重，这里则填写1000000 */
        public BloomFileter(int dataCount) { 
            this(MisjudgmentRate.MIDDLE, dataCount, null);
        }
     
        /** * @param rate 一个枚举类型的误判率 * @param dataCount 预期处理的数据规模，如预期用于处理1百万数据的查重，这里则填写1000000 * @param autoClearRate 自动清空过滤器内部信息的使用比率，传null则表示不会自动清理， * 当过滤器使用率达到100%时，则无论传入什么数据，都会认为在数据已经存在了 * 当希望过滤器使用率达到80%时自动清空重新使用，则传入0.8 */
        public BloomFileter(MisjudgmentRate rate, int dataCount, Double autoClearRate) { 
            long bitSize = rate.seeds.length * dataCount;
            if (bitSize < 0 || bitSize > Integer.MAX_VALUE) { 
                throw new RuntimeException("位数太大溢出了，请降低误判率或者降低数据大小");
            }
            this.rate = rate;
            seeds = rate.seeds;
            size = (int) bitSize;
            notebook = new BitSet(size);
            this.autoClearRate = autoClearRate;
        }
     
        public void add(String data) { 
            checkNeedClear();
     
            for (int i = 0; i < seeds.length; i++) { 
                int index = hash(data, seeds[i]);
                setTrue(index);
            }
        }
     
        /** * 如果不存在就进行记录并返回false，如果存在了就返回true * * @param data * @return */
        public boolean addIfNotExist(String data) { 
            checkNeedClear();
     
            int[] indexs = new int[seeds.length];
            // 先假定存在
            boolean exist = true;
            int index;
     
            for (int i = 0; i < seeds.length; i++) { 
                indexs[i] = index = hash(data, seeds[i]);
     
                if (exist) { 
                    if (!notebook.get(index)) { 
                        // 只要有一个不存在，就可以认为整个字符串都是第一次出现的
                        exist = false;
                        // 补充之前的信息
                        for (int j = 0; j <= i; j++) { 
                            setTrue(indexs[j]);
                        }
                    }
                } else { 
                    setTrue(index);
                }
            }
     
            return exist;
     
        }
     
        private void checkNeedClear() { 
            if (autoClearRate != null) { 
                if (getUseRate() >= autoClearRate) { 
                    synchronized (this) { 
                        if (getUseRate() >= autoClearRate) { 
                            notebook.clear();
                            useCount.set(0);
                        }
                    }
                }
            }
        }
     
        public void setTrue(int index) { 
            useCount.incrementAndGet();
            notebook.set(index, true);
        }
     
        private int hash(String data, int seeds) { 
            char[] value = data.toCharArray();
            int hash = 0;
            if (value.length > 0) { 
     
                for (int i = 0; i < value.length; i++) { 
                    hash = i * hash + value[i];
                }
            }
     
            hash = hash * seeds % size;
            // 防止溢出变成负数
            return Math.abs(hash);
        }
     
        public double getUseRate() { 
            return (double) useCount.intValue() / (double) size;
        }
     
        /** * 分配的位数越多，误判率越低但是越占内存 * <p> * 4个位误判率大概是0.14689159766308 * <p> * 8个位误判率大概是0.02157714146322 * <p> * 16个位误判率大概是0.00046557303372 * <p> * 32个位误判率大概是0.00000021167340 * * @author lianghaohui */
        public enum MisjudgmentRate { 
            // 这里要选取质数，能很好的降低错误率
            /** * 每个字符串分配4个位 */
            VERY_SMALL(new int[]{ 2, 3, 5, 7}),
            /** * 每个字符串分配8个位 */
            SMALL(new int[]{ 2, 3, 5, 7, 11, 13, 17, 19}), //
            /** * 每个字符串分配16个位 */
            MIDDLE(new int[]{ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53}), //
            /** * 每个字符串分配32个位 */
            HIGH(new int[]{ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
                    101, 103, 107, 109, 113, 127, 131});
     
            private int[] seeds;
     
            private MisjudgmentRate(int[] seeds) { 
                this.seeds = seeds;
            }
     
            public int[] getSeeds() { 
                return seeds;
            }
     
            public void setSeeds(int[] seeds) { 
                this.seeds = seeds;
            }
     
        }
     
        public static void main(String[] args) { 
            BloomFileter fileter = new BloomFileter(7);
            System.out.println(fileter.addIfNotExist("1111111111111"));
            System.out.println(fileter.addIfNotExist("2222222222222222"));
            System.out.println(fileter.addIfNotExist("3333333333333333"));
            System.out.println(fileter.addIfNotExist("444444444444444"));
            System.out.println(fileter.addIfNotExist("5555555555555"));
            System.out.println(fileter.addIfNotExist("6666666666666"));
            System.out.println(fileter.addIfNotExist("1111111111111"));
        }
    }

## 错误率估算 ##

纯数学算法推导，公式参见：布隆过滤器 (Bloom Filter) 详解

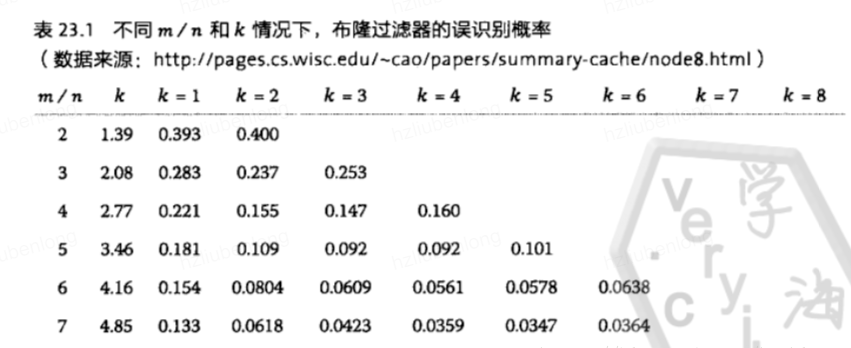
下面给出一个直观的图：

*  m：存储比特位的数组长度（数组长度越长，元素越小，则误判几率越低）注意：m必须>n,不然当只有一个哈希函数的时候都一定会出现hash冲突
 *  n：需要存储转换的元素的个数
 *  K：把元素M映射在数组上哪一位为1的哈希函数的个数。 K要 <= m/n

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2ZneWlidXBp_size_16_color_FFFFFF_t_70 1]

# 参考资料 #

[布隆过滤器(Bloom Filter)的原理和实现][Bloom Filter]  
[布隆过滤器总结（二）原理和例子][Link 1]  
[以太坊源码深入分析（10）-- 以太坊Bloom过滤器实现原理及应用场景分析][10_-- _Bloom]  
[以太坊的工作原理,　干货][Link 2]  
[Bloom Filter(布隆过滤器)的概念和原理（转）][Bloom Filter 1]  
[【原】布隆过滤器 (Bloom Filter) 详解][_Bloom Filter_]

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2ZneWlidXBp_size_16_color_FFFFFF_t_70]: /images/20220325/1b5729d283c14c1cb549fe9ab005e20b.png
[https_archive.codeplex.com_p_bloomfilter]: https://archive.codeplex.com/?p=bloomfilter
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2ZneWlidXBp_size_16_color_FFFFFF_t_70 1]: /images/20220325/cd360f5522b344b89437d8c40d1c45fa.png
[Bloom Filter]: https://blog.csdn.net/yinjing8435/article/details/70537046
[Link 1]: https://blog.csdn.net/lifuxiangcaohui/article/details/42026009
[10_-- _Bloom]: https://www.jianshu.com/p/3e0000add1ae
[Link 2]: https://blog.csdn.net/itchosen/article/details/78655903
[Bloom Filter 1]: https://blog.csdn.net/wxb880114/article/details/81110400
[_Bloom Filter_]: http://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html