等式约束优化与不等式约束优化-蒲公英云

等式约束优化与不等式约束优化

在学习SVM的原理时，接触到了等式约束优化与不等式约束优化，下面是根据相关资料自己总结出来的自己的，希望对大家有所帮助，这是第一篇博客。

1.等式约束优化

1.1.问题描述

当目标函数加上等式约束条件之后，原本的非约束优化变成了等式约束优化，如下：

$\\min\_\{x\} f(x)$ ………………………………………………………………………….(1)

$s.t. \\ \\ \\ h(x)=0$ ………………………………………………………………….(2)

因为存在约束条件，所以将 $f(x)$ 的解限定在了一个可行域的区域，此时可能找不到可以使得 $\\nabla\_xf(x)$ 为0的点，但是我们的目的是找到可行域范围内 $f(x)$ 的最小值即可。

1.2.解法

利用拉格朗日乘子法，引入拉格朗日算子 $\\alpha \\in R^m$ ,构建拉格朗日函数如下：

$L(x,\\alpha)=f(x)+\\alpha\*h(x)$ ………………………………………………….(3)

然后对拉格朗日函数 $L(x,\\alpha)$ 求 $x$ 的偏导，令偏导为0，即：

$\\nabla\_xL(x,\\alpha)=0$ ……………………………………………………………………(4)

对（2）（4）式进行求解即得到此类问题的最优解。

1.3.解释

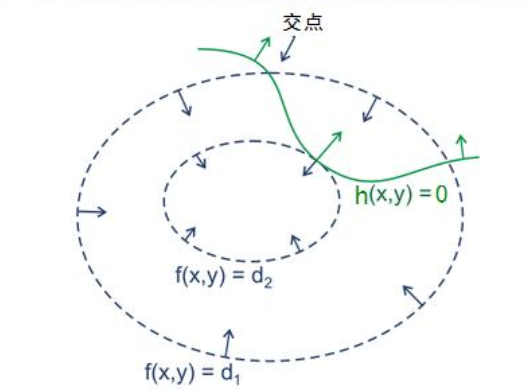
假设我们的目标函数为二维的，即 $f(x,y)$ ，在平面中画出 $f(x,y)$ 的等高线，如下图的虚线所示

显而易见，只有当等高线与目标函数的曲线相切时才有可能得到可行解。因此拉格朗日取得极值的必要条件是目标函数与约束函数相切，这时两者的法向量是平行的，即

$\\nabla\_xf(x)-\\alpha\\nabla\_xh(x)=0$ ……………………………………………………….(5)

所以正好可以得到（3）式，需要注意的是， $\\alpha$ 仅仅要求不等于0即可，正负号不需要确定。

2.不等式约束优化

2.1.问题描述

不等式约束优化问题为：

$\\min\_\{x\} f(x)$ ……………………………………………………………………………….(6)

$s.t. \\ \\ \\ g(x)\\leq0$ ……………………………………………………………………….(7)

2.2.解法

首先构建拉格朗日函数如下：

$L(x,\\alpha)=f(x)+\\beta \*h(x)$ ………………………………………………………(8)

对(8)式关于 $x$ 求偏导，可得

$\\nabla\_xL(x,\\beta)=0$ ………………………………………………………………………..(9)

另外还有KKT条件如下：

    ![\\beta=0 \\ and \\ h(x)> 0][beta_0 _ and _ h_x_ 0]  或者 ![\\beta> 0 \\ and \\ h(x)=0][beta_ 0 _ and _ h_x_0] .....................(10)

由（9）（10）两式可以得出最后的最优解。对于（10）式的解释请看2.3节。

2.3.解释

假设我们的目标函数为二维的，下图给出了目标函数的等高线与不等式约束：

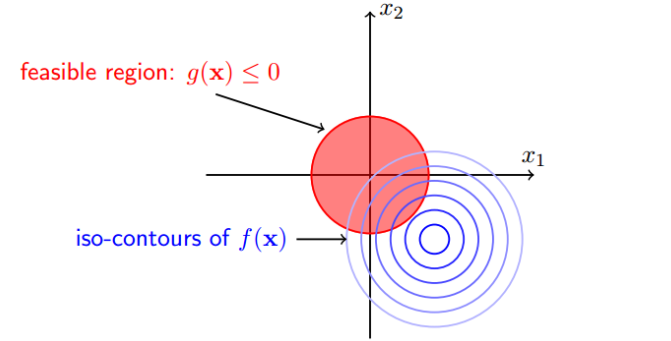
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2xpZGljaGVuZ2ZvMDQxMg_size_16_color_FFFFFF_t_70 1

根据上图可知，可行解存在于 $g(x)< 0$ 或者 $g(x)=0$ 的区域里取到，存在下列两种情况：

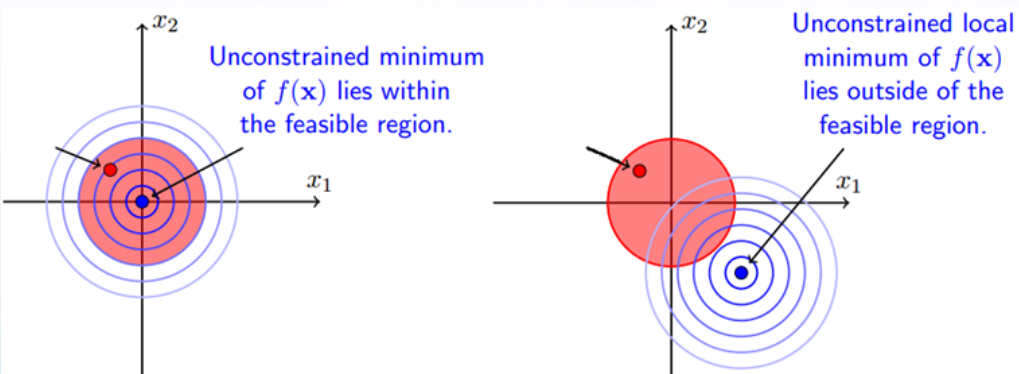
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2xpZGljaGVuZ2ZvMDQxMg_size_16_color_FFFFFF_t_70 2

a)当可行解 $x$ 落在 $g(x)< 0$ 的区域内，此时约束条件不起作用，直接极小化 $f(x)$ 即可，所以（1）式 $L(x,\\alpha)=f(x)+\\beta \*h(x)$ 中，只需满足 $\\beta=0$ 即可。即上图左侧所示.

b)当可行解 $x$ 落在 $g(x)= 0$ 的区域内，此时等价于等式约束优化问题。即上图右侧所示。此时目标函数的梯度方向为指向中心位置的反方向，而约束函数 $h(x)$ 由约束区域指向非约束区域。由下图可以看出，在最优解的位置，约束函数的梯度方向于目标函数的梯度方向正好相反，从而有：

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2xpZGljaGVuZ2ZvMDQxMg_size_16_color_FFFFFF_t_70 3

$\-\\nabla\_xf(x)=\\beta\*\\nabla\_xg(x)$ …………………………………………..(11)

（11）式其实就是（9）式的变形。当然（11）式有一个限制条件 $\\beta> 0$ 。

等式约束优化与不等式约束优化

发表评论取消回复

还没有评论，来说两句吧...

相关阅读

相关六、约束（主键约束、唯一约束、非空约束、检查约束、外键约束）

相关有约束最优化问题 matlab,请教一个Matlab关于有约束最优化问题

相关带等式和不等式约束的线性分式规划Linear-fractional programming

相关四边形不等式优化

相关无约束最优化方法

相关【MySQL-性能优化】--MySQL外键约束简述

相关 Oracle约束：非空约束、主键约束、外键约束、唯一约束和检查约束

相关等式约束优化与不等式约束优化

相关 typescript 类型约束(:普通约束、接口约束、type约束)

相关四边形不等式优化dp

随便看看

推荐Pyramid

HTTP 2.0的那些事

Android APK瘦身之旅

基于JQuery UI的联想输入自动补全

redis详解

Windows下各种java相关开发环境安装Tomcat+Ant

教程文章

热评文章

1江湖小白之一起学Python （二）爬取数据的保存

2Java Shiro：简化身份验证和授权的安全框架

3Java中try()catch{}的使用方法

4Swagger注解-@ApiModel 和 @ApiModelProperty

5windows下强制杀死tomcat进程

6uni-app 条形码(一维码)/二维码生成实现

标签列表