求完全二叉树的结点个数-蒲公英云

求完全二叉树的结点个数

第一次见这个题，看时间小于O(N)。。。。。

只能是二分啊。

但是怎么二分，条件是什么，真的想不到。

后来知道了，我们要找最深一层最右边那个结点。借此确定结点个数。

我们知道，满二叉树的结点个数和深度是有公式的，那么我们找到最后一层最右边的结点，其实就可以确定结点个数。

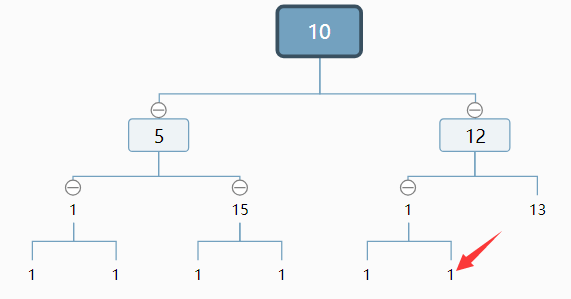
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70

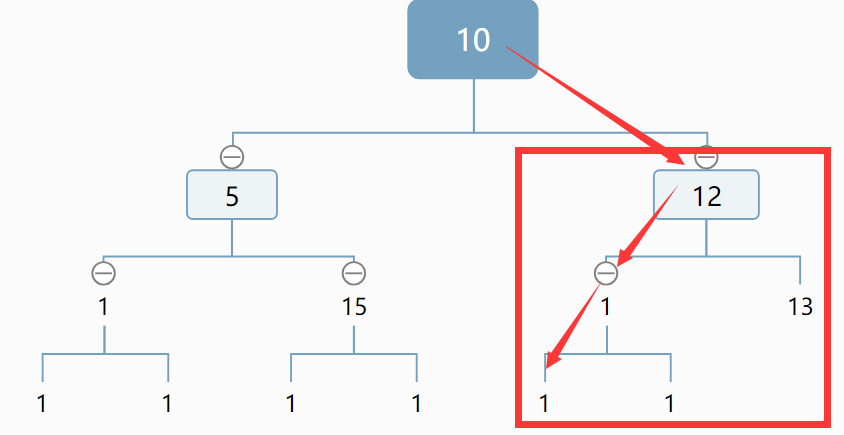
目标：找箭头指向的结点。

我们采用二分法：

1）找到右子树的最左结点

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70 1

如果右子树深度为3（4-1），说明图中最后的1是存在的（说明最后一行最右结点一定来自右子树），否则

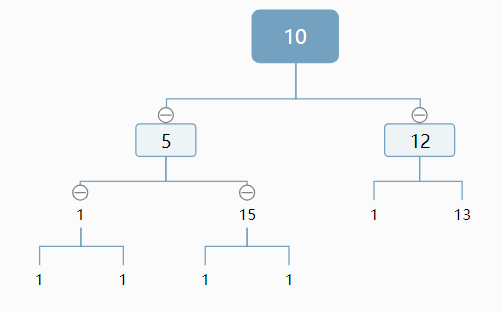
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70 2

右子树深度为2！=4-1，不存在最后一行的结点。（说明最后一行最右结点一定来自左子树）.

判断之后，如果是这种情况，我们排除了左子树，计算排除的结点个数（如图），并对右子树做相同的处理。

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70 1

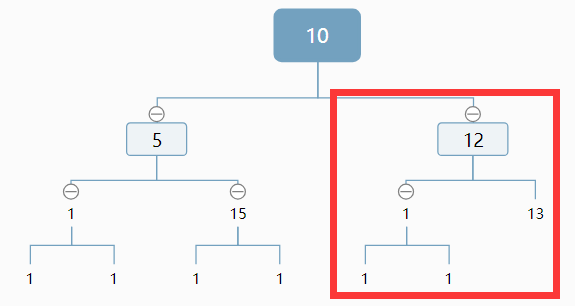
更新结点数（未被框起的部分，满二叉树公式+1）+1是根结点

对方框内重复此过程。

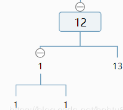
我们继续看右子树，发现右子树深度为1！=3-1.

说明最深层最右结点来自于左子树。所以对左子树重复上述过程

我们发现，右子树深度=1=2（整棵树深度）-1，说明最深层最右结点来自于右子树，所以对右子树重复此过程。

最终找到它

我们再回忆一下过程：

#

1）找到右子树最左节点，确定了深度，对右子树重复。

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70 4

2）找到右子树最左节点，确定了深度，对左子树重复。

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hlYnR1NjY2_size_16_color_FFFFFF_t_70 5

3）找到右子树最左节点，确定了深度，对右子树重复。

4）找到

过程中可以

1）把排除的部分全部加起来，

2）也可以记录每次的选择（向左还是向右），最终100010这种字符，其实就是最后一层的结点个数。

贴上方法1的全部代码：

public class Demo {
    public static class Node {
        public int value;
        public Node left;
        public Node right;
        public Node(int data) {
            this.value = data;
        }
    }
//返回结点个数
    public static int nodeNum(Node head) {
        if (head == null) {
            return 0;
        }
        return bs(head, 1, mostLeftLevel(head, 1));
    }
//返回根为node，当前层数为l，总深度为h的结点个数
    public static int bs(Node node, int l, int h) {
        if (l == h) {
            return 1;
        }
        if (mostLeftLevel(node.right, l + 1) == h) {             //右子树最深一行最左为空
            return (1 << (h - l)) + bs(node.right, l + 1, h);    //右bs+左子树结点个数
        } else {                                                 //右子树最深一行最左不为空
            return (1 << (h - l - 1)) + bs(node.left, l + 1, h);//左bs+右子树结点个数
        }
    }
//计算树的高度
    public static int mostLeftLevel(Node node, int level) {
        while (node != null) {
            level++;
            node = node.left;
        }
        return level - 1;
    }
    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        System.out.println(nodeNum(head));
    }
}