n!的位数

将n!表示成10的次幂，即n!=10^M(10的M次方)，则不小于M的最小整数就是 n!的位数，对该式两边取对数，有 M =log10^n!

由公式log(a*b)=loga+logb，可化为：M = log10^1+log10^2+log10^3…+log10^n

最后将得到的M加上1就是n!的位数。(因为是10^M，所以最后位数要+1)

/* n!位数 */
void problem1()
{
    int n, i;
    double d;
    while (scanf("%d", &n))
    {
        if (n == EOF) break;
        d = 0;
        for (i = 1;i <= n;i++) {
            d += (double)log10(i);
        }
        printf("%d\n", (int)d + 1);
    }
    return;
}

n!末尾0的个数

方法①：其实就是拆分，10可以拆成2*5，所以我们统计所有乘数的因数里min[ n(2) , n(5) ]的个数即可。但阶乘有点特殊的是，5的前面必定有个2（的倍数），故我们求所有乘数的因数里5的个数即可。

方法②：百度后了解的，分享一下：

基于方法①，易得10!里因数5的个数为2 [ 10/5 ]；

而25!里因数5的个数为6，这是因为25=5*5，即25多提供了一个5 [ 25/5 + 25/(5*5) ]；

像125=5*5*5，则125多提供了两个5，所以125!里因数5的个数为: 31 [ 125/5 + 125/(5*5) + 125/(5*5*5) ]。

故，推导公式如下：

while (N)

{

N /= 5；

count += N;

}

/* 求n!末尾0的个数 */
void problem2()
{
    int N, i, mod5, d5, count0 = 0;
    scanf("%d", &N);
        /*  方法①  */
    for (i = 1;i <= N;i++) 
    {
        mod5 = i % 5;
        d5 = i / 5;
        while (mod5 == 0)
        {
            count0++;
            mod5 = d5 % 5;
            d5 /= 5;
        }
    }
        /*  方法②  */
    count0 = 0;
    while (N)
    {
        N /= 5;
        count0 += N;
    }
    printf("%d!的个数 %d\n", N, count0);
}

一只小蜜蜂..

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=2044

有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示：

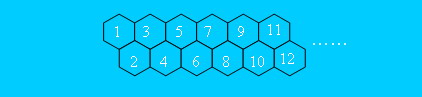
【输入格式】

输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。

【输出格式】

对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

【样例输入】
2
1 2
3 6
【样例输出】
1
3
方法①：简单粗暴地把上下行可能的走法都实现一次，到达终点就输出。注意出口设置。

方法②：除了格子1和格子2，其余数字都是由上个数字走过来或上上个数字走过来，故而累加即可。

/* 一只小蜜蜂.. */
/* 题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=2044 */
int sum_bees = 0; //一只小蜜蜂
void Bees(int a1, int a2, int b1, int b2) //递推,a1起始行，a2起始列，b1终点行，b2终点列
{
    if (a1 == b1 && a2 == b2) { //到达离开
        sum_bees += 1;
        return;
    }
    if (a2 > b2)  return; //剪枝
    if (a1 % 2) //下行
    {
        Bees(a1 - 1, a2 + 1, b1, b2);
        Bees(a1, a2 + 2, b1, b2);
    }
    else { //上行
        Bees(a1 + 1, a2, b1, b2);
        Bees(a1, a2 + 2, b1, b2);
    }
}
void ABee_main()
{
    int a, b, a1, a2, b1, b2;
    int i, j;
    __int64 num[50] = { 0 };
    printf("请输入起/终点a/b：");
    scanf("%d %d", &a, &b); //3 6  0-1 1-3
    printf("请输入解法1或2：");
    scanf("%d", &i);
    switch (i)
    {
    case 1:
        printf("解法1：针对上/下列，各自递推;\n");
                /* 看成是二行X列的数组 */
        b1 = a % 2;a2 = a / 2; //1 1  
        a1 = b % 2;b2 = b / 2; //0 3
        Bees(a1, a2, b1, b2);
        printf("the num:%d\n", sum_bees);
        break;
    case 2:
        printf("解法2：除了1和2，其余数字都是由上个数字走过来或上上个数字走过来，故而累加即可；\n");
        num[1] = 1;num[2] = 2;
        for (j = 3;j <= b - a;j++)  num[j] = num[j - 1] + num[j - 2];
        printf("the num:%I64d\n", num[j - 1]);
        break;
    default:
        printf("输入有误。");
        break;
    }
}

Function Run Fun

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=1331

实现下面的伪代码。另外给定a, b, c，求w(a, b, c)的值。

function w(a, b, c):
       if a <=0 or b <=0 or c <=0, then returns:1
       if a >20or b >20or c >20, then returns: w(20,20,20)
       if a < b and b < c, then returns: w(a, b, c-1)+ w(a, b-1, c-1)- w(a, b-1, c)    
       otherwise it returns: w(a-1, b, c)+ w(a-1, b-1, c)+ w(a-1, b, c-1)

问题在于如果直接计算，对于任意一个三元组(a, b, c)，w(a, b, c)可能被计算多次。但对于固定的(a, b, c)，w(a, b, c)其实是个固定的值，没必要多次计算。所以我们建立一个三维数组 num[21][21][21] ，在每次if判断之前先查表，如果 num[a][b][c] 已存储了计算结果，就直接取出来用，否则就进行之后的递归计算，并把结果存在 num[a][b][c] 里。这样对于任意(a, b, c)就只会计算一次值，此后再遇到就只是查表而已，单次查询的复杂度降到O(1)，总的复杂度为O(n^3)，n为数据规模。这种思路学名【记忆化搜索】。

/* Function Run Fun */
int runfun[21][21][21] = { 0 };
int FunctionRunFun(int a, int b, int c)
{
    if (a <= 0 || b <= 0 || c <= 0)  return 1;
    else if (a > 20 || b > 20 || c > 20) {
        if (runfun[20][20][20] != 0)
        {
            return runfun[20][20][20];
        }
        else
        {
            runfun[20][20][20] = FunctionRunFun(20, 20, 20);
            return runfun[20][20][20];
        }
    }
    else if (a < b&& b < c)
    {
        if (runfun[a][b][c] != 0)
        {
            return runfun[a][b][c];
        }
        else
        {
            runfun[a][b][c] = FunctionRunFun(a, b, c - 1) + FunctionRunFun(a, b - 1, c - 1) - FunctionRunFun(a, b - 1, c);
            return runfun[a][b][c];
        }
    }
    else
    {
        if (runfun[a][b][c] != 0)
        {
            return runfun[a][b][c];
        }
        else
        {
            runfun[a][b][c] = FunctionRunFun(a - 1, b, c) + FunctionRunFun(a - 1, b - 1, c) + FunctionRunFun(a - 1, b, c - 1) - FunctionRunFun(a - 1, b - 1, c - 1);
            return runfun[a][b][c];
        }
    }
}
int main()
{
    int a, b, c;
    scanf("%d %d %d", &a, &b, &c);
    printf("%d\n", FunctionRunFun(a, b, c));
    return 0;
}

饭卡

题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=2546

电子科大本部食堂的饭卡有一种很诡异的设计，即在购买之前判断余额。如果购买一个商品之前，卡上的剩余金额大于或等于5元，就一定可以购买成功（即使购买后卡上余额为负），否则无法购买（即使金额足够）。所以大家都希望尽量使卡上的余额最少。
某天，食堂中有n种菜出售，每种菜可购买一次。已知每种菜的价格以及卡上的余额，问最少可使卡上的余额为多少。

【输入格式】

多组数据。对于每组数据：
第一行为正整数n，表示菜的数量。n<=1000。
第二行包括n个正整数，表示每种菜的价格。价格不超过50。
第三行包括一个正整数m，表示卡上的余额。m<=1000。
n=0表示数据结束。

【输出格式】

对于每组输入,输出一行,包含一个整数，表示卡上可能的最小余额。

【样例输入】
1
50
5
10
1 2 3 2 1 1 2 3 2 1
50
0
【样例输出】
-45
32
背包问题。把可用余额减去5，对菜价进行降序排序，从第二高价的菜品开始搜。

状态转移方程为 dp[ j ] = max(dp[ j ], dp[ j - v[ i ]] + v[ i ])。前者是不买菜，后者是买菜（ j - v[ j ] 即买了菜后的余额），此时已买的菜的总价值dp[ j ]就要加上此次购买的单价v[ j ]。两者之间取价值最大的情况。

最后把买的菜的总价值加上最贵的菜的价值，就是此次购买的金额，则余额也就可求了。

/* 饭卡 */
void MealCard()
{
    int i, j, n, v[1024], money, dp[1024];//菜数、菜价格、余额
    printf("菜数：");
    scanf("%d", &n);
    printf("依次菜价：\n");
    for (i = 0;i < n;i++) scanf("%d", &v[i]);
    printf("余额：");
    scanf("%d", &money);
    if (money < 5)  printf("余额不足!");
    sort(v, v + n, greater<>()); //价格降序
    memset(dp, 0, sizeof(dp)); //初始化数组
    for (i = 1;i < n;i++)
        for (j = money - 5;j >= v[i];j--)
            dp[j] = max(dp[j], dp[j - v[i]] + v[i]);
    printf("the  balance :%d\n", money - dp[money - 5] - v[0]);
}

递增三元组子序列

给出一个无序的整数序列，返回是否存在递增的三元组子序列。
如果存在 i, j, k 使得 arr[i]<arr[j]<arr[k] and 0<i<j<k<n-1，即返回true；如果不存在则返回false。

【样例输入】
1 2 3 4 5
【样例输出】
true
再：【样例输入】
5 4 3 2 1
【样例输出】
false
第一次接触vector。它与数组十分相似，唯一不同的是，vector在需要扩展大小的时候，会自动处理它自己的存储需求。C++Primer的作者说到，在实际的编程中，我们作为程序员应该避免用到低级数组和指针，而更应该多用高级的vector和迭代器。在程序强调速度的情况下，我们程序员可以在类类型的内部使用数组和指针。需要头文件 #include

/* 递增三元组子序列 */
void Solution()
{
    vector<int> nums;
    int i, N, a, b, z;
    scanf("%d", &N);
    for (i = 0;i < N;i++)
    {
        scanf("%d", &z);
        nums.push_back(z);
    }
    a = INT_MAX;b = INT_MAX;
    for (int num : nums) //学到了一种新的循环方式：for(类型 变量名：数组/vector)，等同于for(1 -> n) num = nums[i]
    {
        if (num <= a)  a = num;
        else if (a < num && num <= b)  b = num;
        else
        {
            printf("true\n");
            return;
        }
    }
    printf("false\n");
}

约瑟夫环

30个人围成一圈，由第一个人数起，依次报数，数到第9人，便把他投入大海中。然后再从他的下一个人数起，数到第9人，再将他投入大海中，如此循环，直到剩下15个游客为止。问：哪些位置是将被扔下大海的位置？

emmm…源自https://blog.csdn.net/yanweibujian/article/details/50876631

看的有点迷糊，似懂非懂…

int Josephus1(int N, int k) //从最后一个人下标开始倒推
{
    int i, x = 0; //N前次剩余人数，k临界，x下标
    for (i = 2;i <= N;i++) x = (x + k) % i;
    return x;
}
int Josephus2(int N, int k, int i) //递归，出口是一个人(幸存)的下标
{
    if (i == 1)  return (k - 1 + N) % N;
    //k-1是幸存者的下标(
    else  return (Josephus2(N - 1, k, i - 1) + k) % N;
}
int main()
{
        int N, k;
    scanf("%d %d", &N, &k);
    printf("顺推求法：the survivor: %d\n", Josephus1(N, k));
    printf("递归求法：the survivor: %d\n", Josephus2(N, k, N));
        return 0;
}

母牛的故事

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MTkxODcxMg_size_16_color_FFFFFF_t_70

【广度优先搜索】建立队列搜索每个可能的到达点，需要注意的是要对走过的点做个标记避免死循环。得到的第一个数字即为最小答案。

struct farmer
{
    int x;
    int time;
}farm,now1,next1; //分别是初始位置，当前位置和下一步位置
int judge[200001]; //位置标记
queue <farmer> q; //队列
//宽搜
int bfs(int N,int K,int T) //人、牛、时间
{
    int i;
    farm.x = N, farm.time = 0; //农夫初始化
    while (!q.empty()) q.pop(); //队列清空 
    memset(judge,0,sizeof(judge)); //数组清0
    judge[farm.x] = 1; //标记走过
    q.push(farm);
    while (!q.empty()) //队列非空
    {
        now1 = q.front(); //获取当前位置
        if (now1.x == K) //由于宽搜，故最早获得的必定最小，即答案
        {
            return now1.time;
        }
        q.pop(); //暂时移除队首
        for (i = 0;i < 3;i++)
        {
            next1 = now1; //即将下一步
            /* 循环：0前进，1后退，2闪现 */
            switch (i)
            {
                case 0:
                    ++next1.x;
                    break; 
                case 1:
                    --next1.x;
                    break;
                case 2:
                    next1.x *= 2;
                    break;
                default:
                    break;
            }
            ++next1.time; //计入步数
            if (next1.x == K) // 答案
            {
                return next1.time;
            }
            if (next1.x>=0 && next1.x<=200000 && !judge[next1.x]) //左右没出界 & 没走过
            {
                judge[next1.x] = 1;
                q.push(next1);
            }
        }
    }
    return 0;
}
int main()
{
    int N, K; //位置：N农夫，K牛
    while (~scanf("%d %d", &N, &K))
    {
        printf("%d", bfs(N, K, 0));
    }
    system("pause");
    return 0;
}