汉诺塔问题-蒲公英云

汉诺塔问题

向右看齐 2022-04-17 05:12 384阅读 0赞

问题描述：

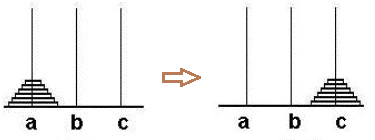
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

问题分析：

先假设除最下面的盘子之外，我们已经成功地将上面的63个盘子移到了b柱，此时只要将最下面的盘子由a移动到c即可。如图：

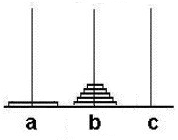
当最大的盘子由a移到c后，b上是余下的63个盘子，a为空。因此现在的目标就变成了将这63个盘子由b移到c。这个问题和原来的问题完全一样，只是由a柱换为了b柱，规模由64变为了63。因此可以采用相同的方法，先将上面的62个盘子由b移到a，再将最下面的盘子移到c……对照下面的过程，试着是否能找到规律：

将b柱子作为辅助，把a上的63个圆盘移动到b上
将a上最后一个圆盘移动到c
将a作为辅助，把b上的62个圆盘移动到a上
将b上的最后一个圆盘移动到c
…..

三个盘子：

四个盘子：

也许你已经发现规律了，即每次都是先将其他圆盘移动到辅助柱子上，并将最底下的圆盘移到c柱子上，然后再把原先的柱子作为辅助柱子，并重复此过程，这个过程称为递归。

伪代码实现：

hanoi(n,A,B,C){
  //n个盘子，柱子A，B，C
  if(n==1) move(A,C);  //只有一个盘子时，直接将A柱上的盘子移动到C柱上
  else{
       hanoi(n-1,A,C,B);//将n-1个盘子由a移动到b，以c为辅助柱子（注意参数顺序）
       move(A,C);//将a上的最后一个盘子移动到c
       hanoi(n-1,B,A,C);//将n-1个盘子由b移动到c，以a为辅助柱子
      }
}

递归算法：

void hanoi(int n,char x,char y,char z){
        if(n == 1)
                move(x,1,z);
        else{
                hanoi(n-1,x,z,y);
                move(x,n,z);
                hanoi(n-1,y,x,z);
        }
}