【Leetcode】132. Palindrome Partitioning II（最少次数将字符串全部切分为回文串）（DP）-蒲公英云

【Leetcode】132. Palindrome Partitioning II（最少次数将字符串全部切分为回文串）（DP）

朱雀 2022-04-25 02:16 266阅读 0赞

Given a string s, partition s such that every substring of the partition is a palindrome.

Return the minimum cuts needed for a palindrome partitioning of s.

Example:

Input: "aab"
Output: 1
Explanation: The palindrome partitioning ["aa","b"] could be produced using 1 cut.

解题思路：

输入一个字符串，将其进行分割，分割后各个子串必须是“回文”结构，要求最少的分割次数。显然，为了求取最少分割次数，一个简单的思路是穷尽所有分割情况，再从中找出分割后可构成回文子串且次数最少的分割方法。

解题思路：

对于输入字符串如s=“aab”,一个直观的思路是判断“aab”是否构成回文，根据回文的特点是对称性，那么，我们可以判断s[0]与s[2]是否相等，不等，因此“aab”不能构成回文，此后再怎么判断呢？？？这种无章法的操作没有意义，因为一个字符串构成回文的情况是很复杂的，对于一个长度为n的字符串，其构成回文的子串长度可能的长度分布范围可以是1—n：整体构成回文如“baab”，则子串长度可为n=4;如“cab”，只能构成长度为1的回文子串。

鉴于上述分析，对于一个字符串，我们需要考虑所有可能的分割，这个问题可以抽象成一个DP问题，对于一个长度为n的字符串，设DP[i][j]表示第i个字符到第j个字符是否构成回文，若是，则DP[i][j]=1;若否，则DP[i][j]=0;如此，根据回文的约束条件（对称性），DP[i][j]构成回文需满足：

1、输入字符串s[i]==s[j],对称性；

2、条件1满足并不能保证i到j构成回文，还须：（j-i）<=1或者DP[i+1][j-1]=1；即，i、j相邻或者i=j，也就是相邻字符相等构成回文或者字符自身构成回文，如果i、j不相邻或者相等，i到j构成回文的前提就是DP[i+1][j-1]=1.

所以状态转移方程：DP[i][j]=(s[i]==s[j]&&(j-i<=1||DP[i+1][j-1]==1))。由于i必须小于j，i>=0&&ij，为无意义部分；绿色部分i==j，即字符串自身必然构成回文，DP[i][j]=1;白色部分，为长度大于1的子串，需要状态转移方程进行判断。

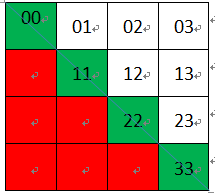
Center

经过判断，得到状态矩阵：绿色部分，即字符串“baab”可构成的回文子串分割情况：绿色部分DP[0][0]、DP[1][1]、DP[2][2]和DP[3][3]构成的是单字符回文子串，DP[1][2]和DP[0][3]构成的是多字符回文子串。

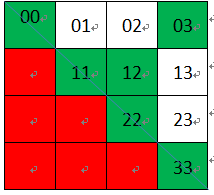
Center 1

在得到输入字符串的所有回文子串的分割情况之后，我们需要考虑如何求取回文子串的最小分割次数，显然，回文子串越长，分割次数越少，因此，分割的时候回文子串应分别取最大长度，如上面的例子，s=”baab”，可行的分割情况有三种：（显然，最少分割次数为0，当然，根据DP[][]矩阵可以很容易求取最长回文子串！！！！）。

1、{DP[0][0]、DP[1][1]、DP[2][2]、DP[3][3]}；

2、{DP[0][0]、DP[1][2]、DP[3][3]}；

3、{DP[0][3]}

当输入字符串所有可能的分割情况求出来之后，我们需要进一步寻找最少分割次数，我们可以用一个一维数组来存储分割次数：设int[] cut=new int[s.length()+1],cut[i]表示第i个字符到最后一个字符所构成的子串的最小分割次数，这里的i有约束条件，就是第i个位置必须是可进行回文分割的，即DP[i][j]==1 (j>=i&&j<s.length()),故：

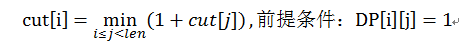
Center 2

class Solution {
public:
    int minCut(string s) 
    {
        int sLen = s.length();
        bool pal[sLen][sLen];
        memset(pal, 0, sizeof(bool)*sLen*sLen);
        int minCuts[sLen];
        for(int i = sLen-1; i >= 0; --i)
        {
            minCuts[i] = INT_MAX;
            for(int j = i; j < sLen; ++j)
            {
                if(s[i]==s[j] && (j-i<2 || pal[i+1][j-1]))
                {
                    pal[i][j] = 1;
                    if(j == sLen-1) minCuts[i] = 0;
                    else minCuts[i] = min(minCuts[i], minCuts[j+1]+1);
                }
            }
        }
        return minCuts[0];
    }
};