二叉树的遍历方式（递归、非递归）—

二叉树作为一种常用的数据结构，也是面试经常被问到的知识点，了解二叉树的结构和性质也是很有必要的，对于众多的树结构，二叉树只是入门的一种，先把二叉树理解通透，再深入学习时，会更简单一些。

二叉树的性质：

(1) 在非空二叉树中，第i层的结点总数不超过 , i>=1；

(2) 深度为h的二叉树最多有

个结点(h>=1)，最少有h个结点；

(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

(4) 具有n个结点的完全二叉树的深度为（注：[ ]表示向下取整）

(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

若I为结点编号则如果I>1，则其父结点的编号为I/2；

如果2*I<=N，则其左孩子（即左子树的根结点）的编号为2*I；若2*I>N，则无左孩子；

如果2*I+1<=N，则其右孩子的结点编号为2*I+1；若2*I+1>N，则无右孩子。

(6)给定N个节点，能构成h(N)种不同的二叉树。

h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。

(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i

相关术语：

树的结点（node）：包含一个数据元素及若干指向子树的分支；

孩子结点（child node）：结点的子树的根称为该结点的孩子；

双亲结点：B 结点是A 结点的孩子，则A结点是B 结点的双亲；

兄弟结点：同一双亲的孩子结点；堂兄结点：同一层上结点；

祖先结点: 从根到该结点的所经分支上的所有结点子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙结点层：根结点的层定义为1；根的孩子为第二层结点，依此类推；

树的深度：树中最大的结点层

结点的度：结点子树的个数

树的度：树中最大的结点度。

叶子结点：也叫终端结点，是度为 0 的结点；

分枝结点：度不为0的结点；

有序树：子树有序的树，如：家族树；

无序树：不考虑子树的顺序；

看完二叉树的性质和相关属于，再来看一下二叉树的遍历。二叉树有很多种遍历方法，最基本的有三种：

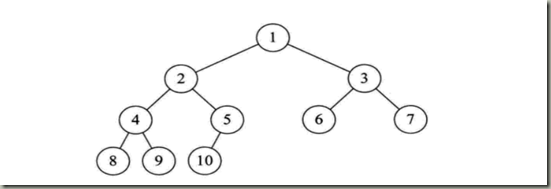
1.前序遍历：对于下图二叉树的前序遍历结果为：1 2 4 8 9 5 10 3 6 7

2.中序遍历：对于下图二叉树的中序遍历结果为：8 4 9 2 10 5 1 6 3 7

3.后序遍历：对于下图二叉树的后序遍历结果为：8 9 4 10 5 2 6 7 3 1

一、前序遍历

基本思想：先访问根结点，再先序遍历左子树，最后再先序遍历右子树。

代码实现：

递归方法

/**
public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val) {
        this.val = val;
    }
}
*/
private void preOrderBinTree(TreeNode root) {
    if (root == null) return;
    System.out.print(root.val + "  ");        //输出结果  1  2  4  8  9  5  10  3  6  7 
    if (root.left != null)
        preOrderBinTree(root.left);
    if (root.right != null)
        preOrderBinTree(root.right);
}

非递归，用栈实现

private void preIterateBinTree(TreeNode root) {
    if(root == null) return;
    Stack<TreeNode> s = new Stack<>();
    TreeNode node = root;
    while (node != null || s.size() > 0) {
        if (node != null) {
            System.out.print(node.val + "  ");
            s.push(node);
            node = node.left;
        } else {
            node = s.pop();
            node = node.right;
        }
    }
}

二、中序遍历

基本思想：先中序遍历左子树，然后再访问根结点，最后再中序遍历右子树即 左—根—右。

递归方法

private void inOrderBinTree(TreeNode root) {
    if (root == null) return;
    if (root.left != null)
        inOrderBinTree(root.left);
    System.out.print(root.val + "  ");        //输出 8  4  9  2  10  5  1  6  3  7
    if (root.right != null)
        inOrderBinTree(root.right);
}

非递归，用栈实现

private void inIterateBinTree(TreeNode root) {
    if(root == null) return;
    Stack<TreeNode> s = new Stack<>();
    TreeNode node = root;
    while (node != null || s.size() > 0) {
        if (node != null) {
            s.push(node);
            node = node.left;
        } else {
            node = s.pop();
            System.out.print(node.val + "  ");
            node = node.right;
        }
    }
}

三、后序遍历

基本思想：先后序遍历左子树，然后再后序遍历右子树，最后再访问根结点即左—右—根。

递归实现

private void afterOrderBinTree(TreeNode root) {
    if (root == null) return;
    if (root.left != null)
        afterOrderBinTree(root.left);
    if (root.right != null)
        afterOrderBinTree(root.right);
    System.out.print(root.val + "  ");        //输出 8  9  4  10  5  2  6  7  3  1
}

非递归，栈实现

private void afterIterateBinTree(TreeNode root) {
    Stack<TreeNode> stack1 = new Stack<>();
    Stack<Integer> stack2 = new Stack<>();
    int i = 1;
    while(root != null || !stack1.empty()) {
        while (root != null) {
            stack1.push(root);
            stack2.push(0);
            root = root.left;
        }
        while(!stack1.empty() && stack2.peek() == i)
        {
            stack2.pop();
            System.out.print(stack1.pop().val + "  ");
        }
        if(!stack1.empty())
        {
            stack2.pop();
            stack2.push(1);
            root = stack1.peek();
            root = root.right;
        }
    }
}

四、层次遍历

非递，队列归实现

private void layerIterateBinTree(TreeNode root) {
    if(root == null) return;
    Queue<TreeNode> q = new ArrayDeque<>();
    TreeNode node = root;
    while (node != null || !q.isEmpty()) {
        if (node != null) {
            System.out.print(node.val + "  ");    //输出 1  2  3  4  5  6  7  8  9  10  
            if(node.left != null)
                q.add(node.left);
            if(node.right != null)
                q.add(node.right);
            node = null;
        } else {
            node = q.remove();
        }
    }
}