数据结构之图论之深搜广搜-蒲公英云

数据结构之图论之深搜广搜

一、问题引入

有一天，小哈一个人去玩迷宫。但是方向感不好的小哈很快就迷路了。小哼得知后便去解救无助的小哈。此时的小哼已经弄清楚了迷宫的地图，现在小哼要以最快的速度去解救小哈。那么，问题来了…

二、问题的分析

首先我们用一个二维数组来存储这个迷宫，刚开始的时候，小哼处于迷宫的入口处（1,1），小哈在（p,q）。其实这道题的的本质就在于找从（1,1）到（p,q）的最短路径。

此时摆在小哼面前的路有两条，我们可以先让小哼往右边走，直到走不通的时候再回到这里，再去尝试另外一个方向。

在这里我们规定一个顺序，按照顺时针的方向来尝试（即右→下→左→上）。

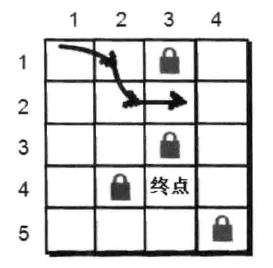
我们先来看看小哼一步之内可以到达的点有哪些？只有（1,2）和（2,1）。

根据刚才的策略，我们先往右边走，但右边（1,3）有障碍物，所以只能往下（2,2）这个点走。但是小哈并不在（2,2）这个点上，所以小哼还得继续往下走，直至无路可走或者找到小哈为止。

注意：并不是让我们找到小哈此题就解决了。因为刚才只是尝试了一条路的走法，而这条路并不一定是最短的。刚才很多地方在选择方向的时候都有多种选择，因此我们需要返回到这些地方继续尝试往别的方向走，直到把所有可能都尝试一遍，最后输出最短的一条路径。

例如下图就是一条可行的搜索路径：

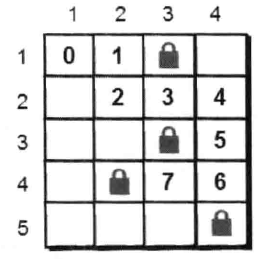
这道题可以有两种解法，一种是dfs，一种是bfs。粘贴代码，首先是dfs：

20分钟hou ::::: 自己代码找不到了，分分钟手写一个：

//广度优先搜索解救小哈 
//众所周知：深搜用栈广搜用队列。 
#include<bits/stdc++.h>
using namespace std;
int a[51][51],v[51][51],m,n,p,q,minn=9999;
int next[4][2]={
   {0,1},{1,0},{0,-1},{-1,0}};
void dfs(int tx,int ty,int step)
{
    if(tx==p&&ty==q){
        if(step<minn)minn=step;
        return ;
    }
    for(int i=0;i<4;i++){
        int x,y;
        x=tx+next[i][0];
        y=ty+next[i][1];
        if(x<1||y<1||x>n||y>m)continue;
        if(a[x][y]==0&&v[x][y]==0){
            v[x][y]=1;
            dfs(x,y,step+1);
            v[x][y]=0;
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin>>a[i][j];
    cin>>p>>q;
    v[1][1]=1;
    dfs(1,1,0);
    cout<<minn;
    return 0;
}

下面是广搜的解法：

广度优先搜索解救小哈 
众所周知：深搜用栈广搜用队列。 
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstdlib>
using namespace std;
int a[51][51]={},n,m,v[51][51]={},p,q;//迷宫，状态数组，初始化 
struct que{
    int x;
    int y;
    int step;
}queue[2505];//手写队列 
int main()
{
    int head=1,tail=2,x,y;
    cin>>m>>n;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            cin>>a[i][j];//输入迷宫，障碍物输入1，其他为0； 
    a[1][1]=1;
    v[1][1]=1;
    queue[1].x=1;
    queue[1].y=1;
    queue[1].step=0;//第一个入队 
    int next[4][2]={
   {0,1},{1,0},{0,-1},{-1,0}};//能够遍力四个方面 
    bool flag=false;
    while(head<tail)
    {    
        for(int i=0;i<4;i++){
            x=queue[head].x+next[i][0];
            y=queue[head].y+next[i][1];
            if(x<1||y<1||x>n||y>m)continue;//判断是否越界 
            if((a[x][y]==0)&&(v[x][y]==0)){//判断是否可行 
                v[x][y]=1; //标记 
                queue[tail].x=x;
                queue[tail].y=y;
                queue[tail].step=queue[head].step+1;
                tail++;//队尾加1 
            }
            if(x==p&&y==q){
                flag=true;
                break;
            }//得到结果 
        }
        if(flag)break;//退出循环 
        head++;//该点已经遍历完毕，出队 
    }
    cout<<queue[--tail].step;//打印！ 
    return 0;    
}