poj Fibonacci 矩阵快速幂-蒲公英云

poj Fibonacci 矩阵快速幂

向右看齐 2022-05-16 11:22 299阅读 0赞

题目链接：点我
Description

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1
Sample Output

0
34
626
6875
Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

大佬博客：点我
这里应用到矩阵快速幂，矩阵快速幂是用来求解递推式的，所以第一步先要列出递推式:
f(n)=f(n-1)+f(n-2)；第二步是建立矩阵递推式，找到转移矩阵: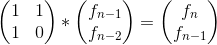 这里写图片描述 ,简写成T * A(n-1)=A(n)，T矩阵就是那个2 乘2的常数矩阵，而
这里就是个矩阵乘法等式左边:1f(n-1)+1f(n-2)=f(n);1f(n-1)+0f(n-2)=f(n-1);

这里还是说一下构建矩阵递推的大致套路,一般An与A(n-1)都是按照原始递推式来构建的，当然可以先猜一个An,主要是利用矩阵乘法凑出矩阵T,第一行一般就是递推式，后面的行就是不需要的项就让与其的相乘系数为0。矩阵T就叫做转移矩阵(一定要是常数矩阵),它能把A(n-1)转移到A(n);然后这就是个等比数列，直接写出通项:此处A1叫初始矩阵。所以用一下矩阵快速幂然后乘上初始矩阵就能得到An,这里An就两个元素(两个位置)，根据自己设置的A(n)对应位置就是对应的值，按照上面矩阵快速幂写法，res[1][1]=f(n)就是我们要求的。

这里给出实现代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
#include<map>
#include<vector>
#include<queue>
#include<set>
#include<iomanip>
#include<cctype>
using namespace std;
const int MAXN=2e5+5;
const int INF=1<<30;
//const long long mod=1e9+7;
#define ll long long
#define edl putchar('\n')
#define sscc ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define FOR(i,a,b) for(int i=a;i<=b;i++)
#define ROF(i,a,b) for(int i=a;i>=b;i--)
#define FORLL(i,a,b) for(ll i=a;i<=b;i++)
#define ROFLL(i,a,b) for(ll i=a;i>=b;i--)
#define mst(a) memset(a,0,ssizeof(a))
#define mstn(a,n) memset(a,n,ssizeof(a))
#define zero(x)(((x)>0?(x):-(x))<eps)
ll mod=10000;
const int ssize=2;
struct Matrix {
    ll a[ssize][ssize];
    Matrix() {
        memset(a,0,sizeof(a));
    }
    void init() {
        for(int i=0; i<ssize; i++)
            for(int j=0; j<ssize; j++)
                a[i][j]=(i==j);
    }
    Matrix operator + (const Matrix &B)const {
        Matrix C;
        for(int i=0; i<ssize; i++)
            for(int j=0; j<ssize; j++)
                C.a[i][j]=(a[i][j]+B.a[i][j])%mod;
        return C;
    }
    Matrix operator * (const Matrix &B)const {
        Matrix C;
        for(int i=0; i<ssize; i++)
            for(int k=0; k<ssize; k++)
                for(int j=0; j<ssize; j++)
                    C.a[i][j]=(C.a[i][j]+1LL*a[i][k]*B.a[k][j])%mod;
        return C;
    }
    Matrix operator ^ (const ll &t)const {
        Matrix A=(*this),res;
        res.init();
        ll p=t;
        while(p) {
            if(p&1)res=res*A;
            A=A*A;
            p>>=1;
        }
        return res;
    }
};
int main() {
    Matrix a,b;
    int n;
    while(scanf("%d",&n)==1&&n!=-1) {
        a.a[0][0]=1;
        a.a[0][1]=1;
        a.a[1][0]=1;
        a.a[1][1]=0;
        b.a[0][0]=1;
        b.a[1][0]=0;
        if(n<=0){
            cout<<0<<endl;
        }
        else{
            a=a^(n-1);
            b=a*b;
            cout<<b.a[0][0]<<endl;
        }
    }
}