排序算法之堆排序及Java实现-蒲公英云

排序算法之堆排序及Java实现

傷城~ 2022-05-26 04:47 361阅读 0赞

一、排序算法的分类

选择排序（直接选择排序，堆排序）
交换排序（冒泡排序，快速排序）
插入排序（直接插入排序，希尔排序）
归并排序
桶式排序
基数排序

二、堆排序的原理

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序。堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
它的基本思想是将待排序的序列构造成一个大顶堆（或小顶堆）。此时，整个序列的最大值就是堆顶的根节点，将其与堆数组的末尾元素交换，此时末尾元素就是最大值，然后将剩余的 n-1 个序列重新构造成一个最大堆，再将新的最大堆的顶与末尾元素交换，如此反复执行，便能得到一个有序序列了。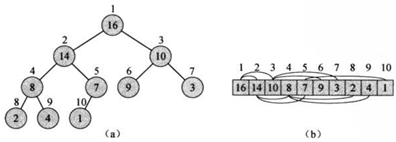
这里写图片描述

三、堆排序的实现

堆排序中重要的一个部分是不断调整堆使其满足最大堆的性质，即父节点都比子节点的值大。调整最大堆的算法如下所示，输入为一个数组A和一个下标i，它用来维护以下标i为根结点的子树最大堆的性质，通过让A[i]的值在最大堆中“逐级下降”，从而使得以下标i为结点的子树重新遵循最大堆的性质。

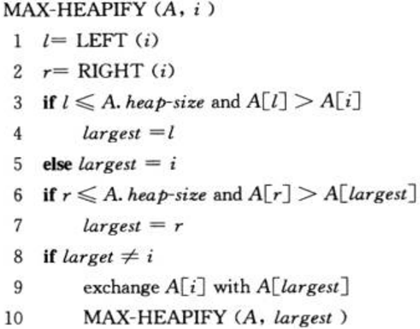
这里写图片描述

之后用置底向上的方法利用MAX-HEAPIFY把一个大小为n=A.length的数组A[1~n]转化为最大堆。算法如下所示，原理很简单，就是从倒数第2层开始，调用MAX-HEAPFY方法，直至到根结点。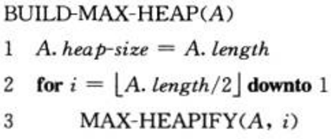
这里写图片描述

最后是取出最大值的算法，也就说将最大堆的顶值与最后一个节点值交换，这样最后一个节点就变成了最大值，再将前n-1个值重新进行最大堆排序。算法如下所示，首先将待排序的数组构建为最大堆数组，之后遍历整棵树，每次遍历“取出”根结点，再调用MAX-HEAPIFY维护子树的最大堆性质。这样就能保证遍历时每次“取出”的元素是当前剩余元素中最大的。

这里写图片描述

实现代码如下所示：

public class HeapSort {
    public static void heapSort(int[] arr){
        buildMaxHeap(arr);
        int heapSize = arr.length;
        //最大值的节点与最后一个节点交换位置
        for (int i = arr.length - 1; i > 0; i--) {
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            //最后一个节点为最大值后，再对前边节点进行堆排序，每交换出一个最大值，最大堆的大小减1
            heapSize--;
            maxHeapify(arr, 0, heapSize);
        }
    }
    /**
     * 4 3 9 5 10 2 6
     * 0 1 2 3 4  5 6
     * 
     *       4
     *   3       9
     * 5   10  2   6 
     * 
     * @param arr 待排序的数组
     * @param index 要进行调整的节点位置
     * @param heapSize 最大堆的大小
     */
    public static void maxHeapify(int[] arr, int index, int heapSize) {
        int leftIndex = 2 * index + 1;//左节点
        int rightIndex = 2 * index + 2;
        int largeIndex;//临时存储三个节点中最大的节点
        if (leftIndex < heapSize && arr[leftIndex] > arr[index]) {
            largeIndex = leftIndex;
        } else {
            largeIndex = index;
        }
        if (rightIndex < heapSize && arr[rightIndex] > arr[largeIndex]) {
            largeIndex = rightIndex;
        }
        if (largeIndex != index) {
            //与最大值的节点交换位置
            int temp = arr[largeIndex];
            arr[largeIndex] = arr[index];
            arr[index] = temp;
            //递归的方式对新的节点进行最大堆调整
            maxHeapify(arr, largeIndex, heapSize);
        }
    }
    //建立最大堆，遍历其中的非叶子节点，调整位置，达到最大堆的特点，即父节点的值大于子节点的值
    public static void buildMaxHeap(int[] arr) {
        int heapSize = arr.length;
        for (int i = (arr.length - 2) / 2; i > -1; i--) {
            maxHeapify(arr, i, heapSize);
        }
    }
    public static void main(String args[]){
        int[] test = {
   4,3,9,5,10,2,6};
        heapSort(test);
        for(int i=0; i<test.length; i++){
            System.out.print(test[i] + " ");
        }
    }
}