计算几何
平面上有有条线段,判断这两条线段是否会相交。
【line.in】
0 0 1 1 0 1 1 0
【line.out】
1
判断线段相交可以用跨立实验+快速排斥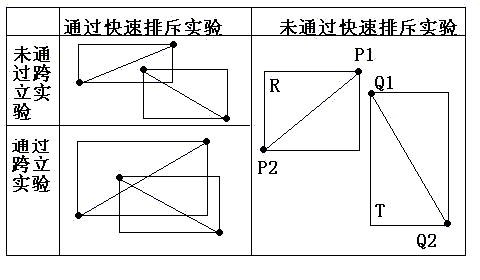
如果是直线,只需要快速排斥就可以判断了(?)。线段有长度,因此还要跨立实验。
快速排斥
if ((max(a.x,b.x)<min(c.x,d.x)||max(a.y,b.y)<min(c.y,d.y)||max(c.x,d.y)<min(a.x,b.x)||max(c,y,d.y)<min(a.y,c.y))return false;
跨立实验:
const double eps = 1e-6;double h, i, j, k;h = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);i = (b.x - a.x) * (d.y - a.y) - (b.y - a.y) * (d.x - a.x);j = (d.x - c.x) * (a.y - c.y) - (d.y - c.y) * (a.x - c.x);k = (d.x - c.x) * (b.y - c.y) - (d.y - c.y) * (b.x - c.x);return h * i <= eps && j * k <= eps;#include<iostream>#include<cstdio>#include<cstdlib>#include<cstring>const double eps = 1e-6;using namespace std;struct point {double x;double y;};inline bool judge(point a, point b, point c, point d){if (max(a.x,b.x)<min(c.x,d.x)||max(a.y,b.y)<min(c.y,d.y)||max(c.x,d.y)<min(a.x,b.x)||max(c.y,d.y)<min(a.y,c.y))return false;double h,i,j,k;h = (b.x - a.x)*(c.y - a.y) - (b.y - a.y) * (c.x - a.x);i = (b.x - a.x)*(d.y - a.y) - (b.y - a.y) * (d.x - a.x);j = (d.x - c.x)*(a.y - c.y) - (d.y - c.y) * (a.x - c.x);k = (d.x - c.x)*(b.y - c.y) - (d.y - c.y) * (b.x - c.x);return (h*i <= eps && j*k <= eps);}int main(){freopen("input.in","r",stdin);point a,b,c,d;scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y);cout<<judge(a,b,c,d);}
B
【问题描述】
小Q对计算几何有着浓厚的兴趣。他经常对着平面直角坐标系发呆,思考一些有趣的问题。今天,他想到了一个十分有意思的题目:
首先,小Q会在x轴正半轴和y轴正半轴分别挑选n个点。随后,他将x轴的点与y轴的点一一连接,形成n条线段,并保证任意两条线段不相交。小Q确定这种连接方式有且仅有一种。最后,小Q会给出m个询问。对于每个询问,将会给定一个点p(px,py),请回答线段OP与n条线段会产生多少个交点?
小Q找到了正在钻研数据结构的你,希望你可以帮他解决这道难题。
【输入格式】
第1行包含一个正整数n,表示线段的数量;
第2行包含n个正整数,表示小Q在x轴选取的点的横坐标;
第3行包含n个正整数,表示小Q在y轴选取的点的纵坐标;
第4行包含一个正整数m,表示询问数量;
随后m行,每行包含两个正整数px,py,表示询问中给定的点的横、纵坐标。
【输出格式】
共m行,每行包含一个非负整数,表示你对这条询问给出的答案。
【样例输入】
3
4 5 3
3 5 4
2
1 1
3 3
【样例输出】
0
3
【数据范围】
对于50%的数据,1≤n,m,≤2×103。
对于100%的数据,1≤n,m≤2×105,坐标范围≤108。
3 4 5
3 4 5
由于情况具有单调性,用二分可优化时间复杂度。利用上面得到的定理,可以用二分+判断来解决这个题目。
#include<iostream>#include<algorithm>#include<string>#include<cstring>#include<cstdio>#include<cstdlib>#include<cmath>#include<queue>#include<list>#define N 200001using namespace std;const double eps = 1e-6;int px,py;int a[N + 10], b[N + 10];struct point {double x;double y;}o,p,f,g;inline bool judge(point a, point b, point c, point d){if (max(a.x,b.x)<min(c.x,d.x)||max(a.y,b.y)<min(c.y,d.y)||max(c.x,d.y)<min(a.x,b.x)||max(c.y,d.y)<min(a.y,c.y))return false;double h,i,j,k;h = (b.x - a.x)*(c.y - a.y) - (b.y - a.y) * (c.x - a.x);i = (b.x - a.x)*(d.y - a.y) - (b.y - a.y) * (d.x - a.x);j = (d.x - c.x)*(a.y - c.y) - (d.y - c.y) * (a.x - c.x);k = (d.x - c.x)*(b.y - c.y) - (d.y - c.y) * (b.x - c.x);return (h*i <= eps && j*k <= eps);}int n,m;int main(){freopen("b.in","r",stdin);freopen("b.out","w",stdout);scanf("%d",&n);for (int i =1;i<=n;i++){scanf("%d",&a[i]);}for (int j=1;j<=n;j++){scanf("%d",&b[j]);}sort(a+1,a+n+1);sort(b+1,b+n+1);scanf("%d",&m);o.x = 0;o.y = 0;for (int i =1;i<=m;i++){scanf("%lf%lf",&p.x,&p.y);int l = 0,r = n;while(l<r){int mid = ((l+r+1)>>1);f.x = 0;f.y = b[mid];//y zhoug.x = a[mid];g.y = 0;//x zhouif (judge(o,p,f,g)){l = mid;}else{r = mid-1;}}printf("%d\n",l);}}//来自http://blog.csdn.net/Donald_TY/article/details/53001702#include<cstdio>#include<iostream>#include<algorithm>#include<cstring>#define ll long longusing namespace std;int n,q;ll x,y;ll a[100005],b[100005];int erfen(int l,int r){if(l>r) return r;int mid=(l+r)/2;if(a[mid]*y>=x*(-1)*b[mid]+a[mid]*b[mid]) return erfen(mid+1,r); else return erfen(l,mid-1);}int main(){cin>>n;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);sort(a+1,a+n+1);for(int i=1;i<=n;i++) scanf("%lld",&b[i]);sort(b+1,b+n+1); //因为线段不相交,所以x与y必须递增cin>>q;for(int i=1;i<=q;i++){scanf("%lld%lld",&x,&y);printf("%d\n",erfen(1,n));}return 0;}
































还没有评论,来说两句吧...