数据结构——基本栈的模板类
数据结构笔记
这篇文章主要是给出栈的基本操作的代码(如: POP、PUSH等),是一个最基本的栈的模板类。
#include <iostream>#include <cassert>#include "stack.h"using namespace std;const int stackIncreament = 20; //栈溢出时扩展空间的增量template<class T>class SeqStack :public Stack<T> {public:SeqStack(int sz = 50); //建立一个空栈~SeqStack(); //析构函数void Push(const T & x); //如果IsFull则溢出处理,否则把x推入栈顶bool Pop(T & x); //如果IsEmpty则不执行,返回false,否则推掉栈顶元素并返回true//推出元素值通过引用参数x返回bool getTop(T & x)const; //如果栈为NULL则返回false,否则返回true,栈顶元素的值通过x传回bool IsEmpty()const; //如果栈中元素等于0个返回true,否则返回falsebool IsFull()const; //如果栈中元素等于maxSize,返回true,否则返回falseint getSize()const; //返回栈中元素的个数void makeEmpty(); //清空栈的内容void output(ostream & os);private:T *elements; //存放栈中元素的栈数组int top; //标记栈的topint maxSize; //栈的最大能容元素的个数void overflowProcess(); //栈的溢出处理};template<class T>void SeqStack<T>::output(ostream & os) {os << "top = " << top << endl;for (int i = 0; i <= top; i++) {os << i << ":" << elements[i] << endl;}}template<class T>ostream & operator << (ostream & os, SeqStack<T> & s) {s.output(os);return os;}template<class T>SeqStack<T>::~SeqStack() {delete[] elements;}template<class T>bool SeqStack<T>::IsEmpty() const {//判断是否为NULLif (-1 == top) {return true;}else {return false;}}template<class T>bool SeqStack<T>::IsFull() const {//判断栈是否FULLif (maxSize - 1 == top) {return true;}else {return false;}}template<class T>void SeqStack<T>::makeEmpty() {//清空栈top = -1;}template<class T>int SeqStack<T>::getSize()const {return top + 1;}template<class T>SeqStack<T>::SeqStack(int sz) {top = -1;maxSize = sz;//建立一个最大尺寸为sz的空栈,若分配不成功则错误处理elements = new T[maxSize]; //创建栈的数组空间assert(elements != NULL); //断言:动态存储分配是否成功}template<class T>void SeqStack<T>::overflowProcess() {//私有函数:扩充栈的存储空间T * newArray = new T[maxSize + stackIncreament];if (NULL == newArray) {cerr << "内存分配错误" << endl;exit(1);}for (int i = 0; i <= top; i++) {newArray[i] = elements[i]; //将原来栈中的数据逐一copy}maxSize += stackIncreament; //更新栈的最大容量delete[] elements; //释放原来的指针elements = newArray; //更新原来的指针}template<class T>void SeqStack<T>::Push(const T& x) {//若栈不满,则将元素x推入栈顶位置,否则溢出处理if (IsFull()) {overflowProcess(); //检测到栈满,扩充栈的容量}elements[++top] = x; //先执行top+1,后元素进栈}template<class T>bool SeqStack<T>::Pop(T & x) {//若栈不空则函数返回栈顶的值,并将栈顶元素弹出if (IsEmpty()) {return false;}x = elements[top--]; //top-1实现pop栈顶元素return true;}template<class T>bool SeqStack<T>::getTop(T &x)const {//若栈不空,则函数返回栈顶元素if (IsEmpty()) {return false;}x = elements[top];return true;}int main(){int pop1, pop2;SeqStack<int> stackTest;stackTest.Push(1);stackTest.Push(2);stackTest.Push(2);stackTest.Push(2);stackTest.Push(5);cout << stackTest;stackTest.Pop(pop1);stackTest.Pop(pop2);cout << stackTest;cout << stackTest.getSize() << endl;int top;stackTest.getTop(top);cout << top << endl;system("pause");return 0;}
运行测试: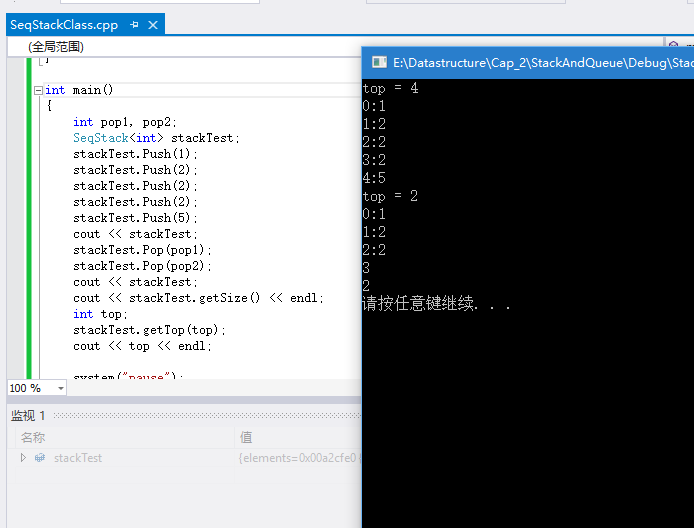
在写这部分程序中,应该注意的是对输出操作符的重载,在涉及友元函数及其它方式时应该注意的问题,之后会有相应的总结。


























![[C#版剑指offer]旋转数组的最小数字查询 [C#版剑指offer]旋转数组的最小数字查询](https://image.dandelioncloud.cn/dist/img/NoSlightly.png)


还没有评论,来说两句吧...