算法-排序算法总结

短命女 2022-06-09 01:58 376阅读 0赞

冒泡排序

朴素冒泡排序

反复扫描待排序序列，在扫描的过程中顺次比较相邻的两个元素的大小，若逆序就交换位置。第一趟，从第一个数据开始，比较相邻的两个数据，（以升序为例）总是把大的数交换到后面，得到一个最大数据在末尾；然后进行第二趟，只扫描前n-1个元素，得到次大的放在倒数第二位。以此类推，最后得到升序序列。
当然也可以从最后一个数开始向前扫描，此时要把较小的数换到前面，得到一个最小的数在最前面；然后进行第二趟，只扫描后n-1个元素，得到次小的放在第二位。以此类推，得到升序序列。
无论是找最大还是找最小，冒泡排序都是一个数从底部逐位移到顶部，就像气泡一样，这也就是冒泡排序的名字由来。

  1. void BubbleSort_simple(int array[], int length)
  2. {
  4.     int temp;       //保存临时数据（数据交换时使用）
  5.     for(int i = 0; i < length-1; i++)//设置需要扫描的趟数
  6.     {
  8.         for(int j = 0; j < length - i - 1; j++) //遍历，比相邻两个数据的大小
  9.         {
  11.             if(array[j] > array[j+1])
  12.             {
  14.                 temp = array[j+1];
  15.                 array[j+1] = array[j];
  16.                 array[j] = temp;
  17.             }
  18.         }
  19.     }
  20. }

改进冒泡排序

对于朴素冒泡排序算法，永远在进行从从n-1到1扫描过程，哪怕中间某次的时候，顺序就已经排好了（不再有交换），所以可以根据这点对冒泡排序作出改进，的如果在某次扫描过程中，发现没有交换，说明已经排好序列，直接终止扫描。所以最多进行n-1趟扫描，最少只需要1趟。

  1. void BubbleSort_Improve(int array[], int length)
  2. {
  4.     int temp;       //保存临时数据（数据交换时使用）
  5.     bool flag = true;       //设置标记，记录此趟排序是否发生交换
  6.     for(int i = 0; i < length-1&&flag; i++)//设置需要扫描的趟数
  7.     {
  9.         flag = false;
  10.         for(int j = 0; j < length - i - 1; j++) //遍历，比相邻两个数据的大小
  11.         {
  13.             if(array[j] > array[j+1])
  14.             {
  16.                 temp = array[j+1];
  17.                 array[j+1] = array[j];
  18.                 array[j] = temp;
  20.                 flag = true;
  21.             }
  22.         }
  23.     }
  24. }

稳定性与复杂度分析

  • 时间复杂度：
    对于朴素冒泡排序算法，没有最好与最差情况的区别，时间复杂度都是 O ( n 2 ) O(n^2) O(n2)，对于改进冒泡排序算法，最好的情况是本来有序，此时时间复杂度为 O ( n ) O(n) O(n)，最差的情况是逆序，此时时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
  • 空间复杂度：
    冒泡排序只需要一个临时位置做交换数据，所以空间复杂度 O ( 1 ) O(1) O(1)。
  • 稳定性：
    稳定

简单选择排序

冒泡排序存在大量的逐位交换操作，这是因为冒泡排序每次逐位比较后，只要满足条件就会发生交换，最后把小的数换到最前。那么一定需要逐位交换吗？能不能先知道某个值最终要放到哪里，然后一次换好？这就是简单选择排序要做的事。
简单选择排序算法就是为了解决频繁交换的问题（虽然这对时间复杂度计算没有影响，但是交换操作实际上在影响着效率）。
选择排序，或者叫简单选择排序（因为堆排序也是一种选择排序），简单选择排序有两个索引，一个是要把最小的值交换到的位置i，一个是找到的最小值位置min，其中i是随着遍历逐步加1的，而每一次的过程中都用i初始化min，并遍历i后的所有个位置逐个与min比较，最终从中找到min的位置后与i交换，i++后重复上述过程，直到遍历结束。

  1. void SelectSort(int array[], int length)
  2. {
  4.     int min;  //保存目标元素的索引
  5.     int temp; //临时变量（数据交换时候使用）
  6.     for(int i = 0; i < length; i++)//对数组中的每一个数进行遍历
  7.     {
  9.         min = i;      //最小值位置等于它本身
  10.         for(int j = i+1; j < length; j++)//选择出目前最小元素的索引
  11.         {
  13.             if(array[min] > array[j])
  14.                 min = j;
  15.         }
  17.         if(min != i)
  18.         {
  20.             temp = array[i];
  21.             array[i] = array[min];
  22.             array[min] = temp;
  23.         }
  24.     }
  25. }

稳定性与复杂度分析

  • 时间复杂度：
    简单选择排序为了解决频繁交换问题，相比于（改进冒泡排序）在时间复杂度上没有改进，其实反而更差一些，因为简单选择排序在时间复杂度上没有最好与最坏的区别，都是 O ( n 2 ) O(n^2) O(n2)，但是比较好的一点是，即便是最差的情况，简单选择排序的交换次数也只有 n − 1 n-1 n−1次。
  • 空间复杂度：
    O ( 1 ) O(1) O(1)
  • 稳定性：
    不稳定

直接插入排序

这里的插入排序指的是直接插入排序算法，基本思想就是认为前i-1个数的顺序已经排好，将第i个值插入到前i-1个中的适当位置。所以i是从数组中第二个数开始一直到最后，每次插入前都保存好array[i]的值，并对前i-1个数的位置做出调整，最后将array[i]插入到合适的位置。

  1. void InsertSort(int array[],int length)
  2. {
  4.     int temp, insert;   //temp保存插入值,insert记录与插入值比较的索引
  5.     for(int i = 1;i < length;i++)
  6.     {
  8.         temp = array[i]; //记录下需要插入的值，防止向后移位时，值被覆盖
  9.         insert = i-1;
  10.         while(insert >= 0 && array[insert] > temp )
  11.         {
  13.             array[insert+1] = array[insert];
  14.             insert = insert - 1;
  15.         }
  16.         array[insert+1] = temp;
  17.     }
  18. }

稳定性与复杂度分析

  • 时间复杂度：
    最好的情况（本身有序），时间复杂度 O ( n ) O(n) O(n)；最差的情况（本身逆序），时间复杂度 O ( n 2 ) O(n^2) O(n2)，平均时间复杂度 O ( n 2 ) O(n^2) O(n2)。
  • 空间复杂度：
    O ( 1 ) O(1) O(1)
  • 稳定性：
    稳定

希尔排序

希尔排序是第一个突破排序时间复杂度 O ( n 2 ) O(n^2) O(n2)的算法，又称缩小增量排序法。基本思想是使用跃进的方式，把待排序序列分成若干较小的子序列，然后逐个使用直接插入排序法排序，最后再对一个较为有序的序列进行一次排序，主要是为了减少移动的次数，提高效率。原理应该就是从无序到渐渐有序，要比直接从无序到有序移动的次数会少一些。
希尔排序比较难理解的地方也是它的跃进式方式，在最外层的循环（do-while）中，是在改变跃进的步长，最后一次的跃进步长一定为1，也就是两两交换。第二层循环（第一个for）实现以某一次的step遍历所有数，而for之内的操作其实就是一个直接插入排序。

  • 希尔排序中的直接插入操作，是在间隔一个阶跃进行子序列操作，13-20行是一个直接插入排序，只是1换成了step。

  • 希尔排序的最后一次do（step =1），一定是退化成直接插入排序，但是这个时候，数列是相对有序的状态。

    void ShellSort(int array[], int length)
    {

    1. int insert,temp;   //temp保存临时数据（数据交换时使用）
    2. int step=length;     //设置增量
    3. do 
    4. {
    6.     step = step/3;      
    7.     //做直接插入排序 将1换成step
    8.     for( int i = step; i < length; i++)
    9.     {
    11.         temp = array[i];
    12.         insert = i-step;
    13.         while(insert>=0&& array[insert] > temp)
    14.         {
    16.             array[insert + step] = array[insert];
    17.             insert-=step
    18.         }
    19.         array[insert + step] = temp;
    20.     }
    21. }
    22. while (step>1);

    }

稳定性与复杂度分析

  • 时间复杂度：
    最好的情况（本身有序），时间复杂度 O ( n 1.3 ) O(n^{1.3}) O(n1.3)；最差的情况（本身逆序），时间复杂度 O ( n 2 ) O(n^2) O(n2)，平均时间复杂度 ( n 1.5 ) (n^{1.5}) (n1.5)。
  • 空间复杂度：
    O ( 1 ) O(1) O(1)
  • 稳定性：
    不稳定

快速排序

快速排序是一个递归的过程，递归的部分一般称为Partition，即在一个序列中选取一个数字n，把序列中小于等于n的数字放在n的左边，大于n的数字放在n 的右边，即完成了一次Partition。其具体的实现为：
比如一个数列arr为：{4,7,8,9,5,6,1,3,2}，那么我们可以直接把arr[0]位置的数作为分割数，即n=4，那么下面的工作就是如何把数列中小于等于4的数放在4的左边，大于等于4的数放在4的右边。首先找到右侧第一个小于等于4的数，与4所在的位置交换：
2 7 8 9 5 6 1 3 4
找到左侧第一个大于等于4的数，与4交换：
2 4 8 9 5 6 1 3 7
找到右侧第一个小于等于4的数，与4交换：
2 3 8 9 5 6 1 4 7
找到左侧第一个大于等于4的数，与4交换：
2 3 4 9 5 6 1 8 7
一直重复上述过程，直到右侧大于等于4的数与左侧小于等于4的数是一个数（一个位置），也就是4本身所在的位置，就完成了一次Partition：
2 3 1 9 5 6 4 8 7
2 3 1 4 5 6 9 8 7
2 3 1 4 5 6 9 8 7
2 3 1 4 5 6 9 8 7

以上就是快速排序算法的基础组成，而快排就是不断递归Partition的过程。

  1. //Partition过程
  2. int Partition(int array[],int low,int high)
  3. {
  5.     int pv = array[low];
  6.     while(low<high)
  7.     {
  9.         //low和pv对应的索引是相同的，先判断高位
  10.         while((low<high)&&(array[high]>=pv)) 
  11.             high--;
  12.         swap(array,high,low);
  13.         while((low<high)&&array[low]<=pv)
  14.             low++;
  15.         swap(array,low,high);
  16.     }
  17.     return low;
  18. }
  19. //递归调用部分
  20. void QSort(int array[],int low,int high)
  21. {
  23.     if (low>=high)
  24.         return;    
  25.     int pvIndex = Partition(array,low,high);
  26.     QSort(array,low,pvIndex-1);
  27.     QSort(array,pvIndex+1,high);
  28. }
  29. void QuickSort(int array[],int length)
  30. {
  32.     QSort(array,0,length-1);
  33. }

稳定性与复杂度分析

  • 时间复杂度：
    最好的情况（本身有序），时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)；最差的情况（本身逆序），时间复杂度 O ( n 2 ) O(n^2) O(n2)，平均时间复杂度 ( n l o g n ) (nlogn) (nlogn)。
  • 空间复杂度：
    O ( n l o g n ) O(nlogn) O(nlogn)
  • 稳定性：
    不稳定

归并排序

归并排序是建立在二路归并和分治法的基础上的一个高效排序算法,将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
将待排序序列R[0…n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列。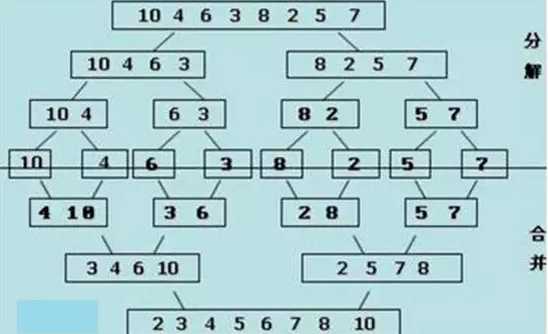
这里写图片描述
所以就像快速排序的Partition功能一样，归并排序也有一个基础的组成部分，就是合并的过程，我们可以将它称为Merge，其思路为：比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

  1. void Merge(int array[],int left,int mid,int right)
  2. {
  4.     int lstart=left;
  5.     int rstart = mid+1;
  6.     int index = 0;
  7.     int *temp = new  int[right-left+1];
  8.     while (lstart<=mid&&rstart<=right)
  9.     {
  11.         if(array[lstart]<=array[rstart])
  12.             temp[index++]=array[lstart++];
  13.         else
  14.             temp[index++]=array[rstart++];
  15.     }
  16.     while (lstart<=mid)
  17.     {
  19.         temp[index++]=array[lstart++];
  20.     }
  21.     while (rstart<=right)
  22.     {
  24.         temp[index++]=array[rstart++];
  25.     }
  26.     for(int i = 0; i < index; i++)
  27.         array[left+i] = temp[i];
  28.     delete[] temp;
  29.     temp = nullptr;
  30. }
  31. void MSort(int array[],int left,int right)
  32. {
  34.          if(left == right) return;
  35.         int mid = (left+right)/2;
  36.         MSort(array,left,mid);
  37.         MSort(array,mid+1,right);
  38.         Merge(array,left,mid,right);
  39. }
  40. void MergeSort(int array[],int length)
  41. {
  43.     MSort(array,0,length-1);
  44. }

稳定性与复杂度分析

  • 时间复杂度：
    最好的情况（本身有序），时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)；最差的情况（本身逆序），时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)，平均时间复杂度 ( n l o g n ) (nlogn) (nlogn)。
  • 空间复杂度：
    在所有的常见排序算法中，归并排序的空间复杂度最高，因为他需要一个和待排序数列相同长度的空间去做拆分和合并，所以空间复杂度为： O ( n ) O(n) O(n)
  • 稳定性：
    稳定
    归并排序也是快排，堆排序，归并排序三种算法中唯一稳定的一个。

堆排序

堆排序是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。所以在理解堆排序之前，要了解堆的概念：
堆分为大根堆和小根堆，是完全二叉树。
若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。完全二叉树度为1的点只有1个或0个
大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。所以根据大根堆的要求可知，最大的值一定在堆顶。与最大堆对应的就是最小堆了，最小堆的要求是每一个节点的值都不小于其父结点的值。堆一般用数组的形式实现，下面就是最大堆与最小堆的存储结构：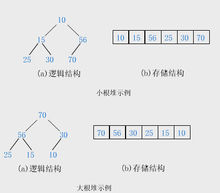
这里写图片描述
可以看到，i结点的父结点下标就为(i – 1) / 2（/符号是取整符号，不是除法！！不是除法！！）。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。比如最大数组中，i=3位置的值为25，那么其父结点为i=1位置，在最大堆中也就是56；i=3结点的左右孩子是i=7和i-8，显然没有。
那么清楚了最大堆与其顺序存储形式后，就可以看下堆排序算法了（假设使用最大堆），那么首先将无序的数组构建成一个最大堆的形式，此时堆顶的元素值一定是最大的，随后移除该值，重新调整成最大堆，重复移除与调整的过程，直到只剩下最后一个结点。

  1. void HeapAdjust(int array[],int parent,int length)
  2. {
  4.     int temp =array[parent];
  5.     for(int child = parent*2+1;child<length;child = child*2+1)
  6.     {
  8.         if(child+1<length&&array[child]<array[child+1])
  9.             child++;
  10.         if(temp>=array[child])
  11.             break;
  12.         array[parent] = array[child];
  13.         parent = child;
  14.     }
  15.     array[parent] = temp;
  16. }
  17. void HeapSort(int array[],int length)
  18. {
  20.     int i;
  21.     for(i=length/2-1;i>=0;i--)
  22.      HeapAdjust(array,i,length-1);
  23.     for (i = length-1;i>0;i--)
  24.     {
  26.         swap(array,0,i);
  27.         HeapAdjust(array,0,i);
  28.     }
  29. }
  31. void HeapAdjust(int array[], int start, int end) 
  32. {
  34.     //建立父节点指标和子节点指标
  35.     int dad = start;
  36.     int son = dad * 2 + 1;
  37.     while (son <= end)  //若子节点指标在范围内才做比较
  38.     {
  40.         if (son + 1 <= end && array[son] < array[son + 1]) //先比较两个子节点大小，选择最大的
  41.             son++;
  42.         if (array[dad] > array[son]) //如果父节点大於子节点代表调整完毕，直接跳出函数
  43.             return;
  44.         else  //否则交换父子内容再继续子节点和孙节点比较
  45.         {
  47.             swap(array,dad, son);
  48.             dad = son;
  49.             son = dad * 2 + 1;
  50.         }
  51.     }
  52. }
  53. void HeapSort(int array[], int length) 
  54. {
  56.     //初始化，i从最后一个父节点开始调整，下标为lenght/2 -1
  57.     for (int i = length/ 2 - 1; i >= 0; i--)
  58.         HeapAdjust(array, i, length- 1);//调整数组从i到最后
  59.     //先将第一个元素和已经排好的元素前一位做交换，再从新调整(刚调整的元素之前的元素)，直到排序完毕
  60.     for (int i = length- 1; i > 0; i--) 
  61.     {
  63.         swap(array,0,i);
  64.         HeapAdjust(array, 0, i - 1);//调整数组从开始到交换好的前一个位置
  65.     }
  66. }

稳定性与复杂度分析

  • 时间复杂度：
    最好的情况（本身有序），时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)；最差的情况（本身逆序），时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)，平均时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)。
  • 空间复杂度：
    O ( 1 ) O(1) O(1)
  • 稳定性：
    不稳定

总结

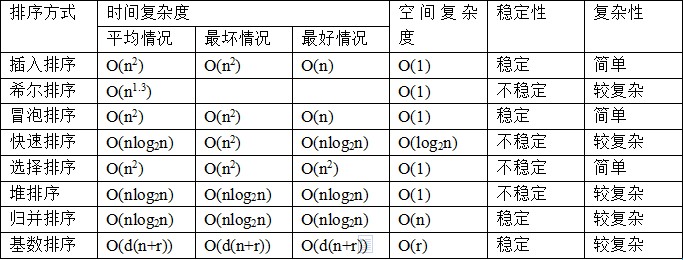
这里写图片描述

所有排序算法中用的最多的是堆排序，快速排序与归并排序，在这三种算法中：
如果从空间复杂度来考虑的话，首选堆排序，其次是快速排序，最后是归并排序。
如果从稳定性考虑，选择归并排序（稳定）。

此外，还有一种说法，如果待排序列表基本有序，那么选择直接插入排序。

在以上的7中排序算法中，也可以按照主要操作进行分类，可以分为4类：

基于交换：冒泡排序，快速排序
基于选择：简单选择排序，堆排序
基于插入：直接插入排序，希尔排序
基于归并：归并排序

在最后，不知道大家有没有发现一个问题，堆排序与快排的空间复杂度，平均时间复杂度与最好情况下时间复杂度都一样，但是最差情况下时间复杂度堆排序要更胜一筹，那么为毛快排更好呢？直接贴出解答地址吧，我也是从这看的：数学之美番外篇：快排为什么那样快

发表评论

表情：
评论列表 （有 0 条评论，376人围观）

还没有评论，来说两句吧...

相关阅读

    相关 排序算法总结

    概述 排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。 我们这里说说八

    ﹏ヽ暗。殇╰゛Y﹏ヽ暗。殇╰゛Y/ 0 赞/ 281 阅读

    相关 算法-排序算法总结

    冒泡排序 朴素冒泡排序 反复扫描待排序序列，在扫描的过程中顺次比较相邻的两个元素的大小，若逆序就交换位置。第一趟，从第一个数据开始，比较相邻的两个数据，（以升序为例

    短命女短命女/ 0 赞/ 377 阅读

    相关 排序算法总结

    1.插入排序算法（附伪代码和C源码） 插入排序原理：从第i=2位开始到数组长度|A|截至。将当前i的值key取出来，从i开始从后往前\[1, i-1\]寻找小于（大

    淩亂°似流年淩亂°似流年/ 0 赞/ 387 阅读

    相关 排序算法总结

    最近在看左神的算法视频，随便记录下自己的学习心得，方便以后review，也让大家对基本的排序算法有个了解。 冒泡排序 > 冒泡排序（英语：Bubble Sort）是一种

    红太狼红太狼/ 0 赞/ 420 阅读

    相关 排序算法总结

    1.冒泡排序 > 　冒泡算法思想： > 　　1.从左到右依次比较相邻的元素。如果第一个比第二个大，就交换他们两个,等全部执行完,最后的元素就是最大的数,这      

    今天药忘吃喽~今天药忘吃喽~/ 0 赞/ 412 阅读

    相关 排序算法总结

    常见排序算法评估 时间复杂度 O(n2)：冒泡排序、选择排序、插入排序 O(nlogn)：归并排序、快速排序、堆排序、希尔排序 O(n)：计数排序、基数排序  

    ╰半橙微兮°╰半橙微兮°/ 0 赞/ 394 阅读