矩形面积并、矩形面积交、矩形周长并（线段树、扫描线总结）

浅浅的花香味﹌ 2022-06-14 09:08 289阅读 0赞

# 转自：http://blog.csdn.net/lwt36/article/details/48908031 #

# HDU 1542 \[POJ 1151\] Atlantis （矩形面积并） #

*  题意:
    
    > 求N<=100个矩形的面积并
 *  分析:
    
    >  *  离散化: 这些技巧都是老生常谈的了, 不然浮点数怎么建树, 离散化x坐标就可以了
    >  *  扫描线: 首先把矩形按y轴分成两条边, 上边和下边, 对x轴建树, 扫描线可以看成一根平行于x轴的直线.   
    >     从y=0开始往上扫, 下边表示要计算面积\+1, 上边表示已经扫过了−1, 直到扫到最后一条平行于x轴的边   
    >     但是真正在做的时候, 不需要完全模拟这个过程, 一条一条边地插入线段树就好了
    >  *  线段树: 用于动态维护扫描线在往上走时, x轴哪些区域是有合法面积的
    >  *  ps:这种线段树是不用lazy的, 因为不用push\_down, 为啥不用push\_down, 因为没有查询操作
 *  扫描线扫描的过程（建议配合代码模拟）
    
    > ps:无论说的再好,都不如自己在纸上模拟一遍扫描的过程,我自己学的时候模拟了很多遍   
    > 以下图转载自@kk303的博客

![初始状态][20151005001227138]

初始状态

![这里写图片描述][20151005001522369]

扫到最下边的线, 点1→3更新为1

![这里写图片描述][20151005001541628]

扫到第二根线, 此时S=lcnt!=0∗h两根线之间, 得到绿色的面积, 加到答案中去, 随后更新计数

![这里写图片描述][20151005001600220]

同上, 将黄色的面积加到答案中去

![这里写图片描述][20151005001615715]

同上, 将灰色的面积加到答案中去

![这里写图片描述][20151005001627502]

同上, 将紫色的面积加到答案中去

![这里写图片描述][20151005001646747]

同上, 将蓝色的面积加到答案中去

*  代码

//
    // Created by TaoSama on 2015-07-14
    // Copyright (c) 2015 TaoSama. All rights reserved.
    //
    //#pragma comment(linker, "/STACK:1024000000,1024000000")
    #include <algorithm>
    #include <cctype>
    #include <cmath>
    #include <cstdio>
    #include <cstdlib>
    #include <cstring>
    #include <iomanip>
    #include <iostream>
    #include <map>
    #include <queue>
    #include <string>
    #include <set>
    #include <vector>
    
    using namespace std;
    #define pr(x) cout << #x << " = " << x << " "
    #define prln(x) cout << #x << " = " << x << endl
    const int N = 205, INF = 0x3f3f3f3f, MOD = 1e9 + 7;
    
    int n;
    struct Seg {
        double l, r, h; int d;
        Seg() {}
        Seg(double l, double r, double h, int d): l(l), r(r), h(h), d(d) {}
        bool operator< (const Seg& rhs) const {
       return h < rhs.h;}
    } a[N];
    
    int cnt[N << 2]; //根节点维护的是[l, r+1]的区间
    double sum[N << 2], all[N];
    
    #define lson l, m, rt << 1
    #define rson m + 1, r, rt << 1 | 1
    
    void push_up(int l, int r, int rt) {
        if(cnt[rt]) sum[rt] = all[r + 1] - all[l];
        else if(l == r) sum[rt] = 0; //leaves have no sons
        else sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
    }
    
    void update(int L, int R, int v, int l, int r, int rt) {
        if(L <= l && r <= R) {
            cnt[rt] += v;
            push_up(l, r, rt);
            return;
        }
        int m = l + r >> 1;
        if(L <= m) update(L, R, v, lson);
        if(R > m) update(L, R, v, rson);
        push_up(l, r, rt);
    }
    
    int main() {
    #ifdef LOCAL
        freopen("in.txt", "r", stdin);
    // freopen("out.txt","w",stdout);
    #endif
        ios_base::sync_with_stdio(0);
    
        int kase = 0;
        while(scanf("%d", &n) == 1 && n) {
            for(int i = 1; i <= n; ++i) {
                double x1, y1, x2, y2;
                scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
                a[i] = Seg(x1, x2, y1, 1);
                a[i + n] = Seg(x1, x2, y2, -1);
                all[i] = x1; all[i + n] = x2;
            }
            n <<= 1;
            sort(a + 1, a + 1 + n);
            sort(all + 1, all + 1 + n);
            int m = unique(all + 1, all + 1 + n) - all - 1;
    
            memset(cnt, 0, sizeof cnt);
            memset(sum, 0, sizeof sum);
    
            double ans = 0;
            for(int i = 1; i < n; ++i) {
                int l = lower_bound(all + 1, all + 1 + m, a[i].l) - all;
                int r = lower_bound(all + 1, all + 1 + m, a[i].r) - all;
                if(l < r) update(l, r - 1, a[i].d, 1, m, 1);
                ans += sum[1] * (a[i + 1].h - a[i].h);
            }
            printf("Test case #%d\nTotal explored area: %.2f\n\n", ++kase, ans);
        }
        return 0;
    }
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91
      
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91

--------------------

# HDU 1255 覆盖的面积 （矩形面积交） #

*  题意:
    
    > 求N<=1000个矩形覆盖至少两次区域的面积,也就是矩形面积交
 *  分析
    
    >  *  前面的与矩形面积并类似, 不同的是push\_up的时候要考虑至少覆盖一次one和至少覆盖两次two的更新   
    >     尤其是当前被覆盖了一次的时候, 由于没有push\_down操作, 父亲节点的信息是没有同步到儿子节点的, 这样的话push\_up就要考虑了.
    >  *  父亲被记录覆盖了一次, 但是如果儿子被覆盖过, 这些操作都是在这个父亲这个大区间上的, 就相当于父亲区间被覆盖了至少两次, 所以two和one都要更新
 *  代码

//
    // Created by TaoSama on 2015-10-04
    // Copyright (c) 2015 TaoSama. All rights reserved.
    //
    //#pragma comment(linker, "/STACK:1024000000,1024000000")
    #include <algorithm>
    #include <cctype>
    #include <cmath>
    #include <cstdio>
    #include <cstdlib>
    #include <cstring>
    #include <iomanip>
    #include <iostream>
    #include <map>
    #include <queue>
    #include <string>
    #include <set>
    #include <vector>
    
    using namespace std;
    #define pr(x) cout << #x << " = " << x << " "
    #define prln(x) cout << #x << " = " << x << endl
    const int N = 2e3 + 10, INF = 0x3f3f3f3f, MOD = 1e9 + 7;
    
    int n;
    struct Seg {
        double l, r, h; int d;
        Seg() {}
        Seg(double l, double r, double h, double d): l(l), r(r), h(h), d(d) {}
        bool operator< (const Seg& rhs) const {
            return h < rhs.h;
        }
    } a[N];
    
    int cnt[N << 2];
    double one[N << 2], two[N << 2], all[N];
    
    #define lson l, m, rt << 1
    #define rson m + 1, r, rt << 1 | 1
    
    void push_up(int l, int r, int rt) {
        if(cnt[rt] >= 2) two[rt] = one[rt] = all[r + 1] - all[l];
        else if(cnt[rt] == 1) {
            one[rt] = all[r + 1] - all[l];
            if(l == r) two[rt] = 0;
            else two[rt] = one[rt << 1] + one[rt << 1 | 1];
        } else {
            if(l == r) one[rt] = two[rt] = 0;
            else {
                one[rt] = one[rt << 1] + one[rt << 1 | 1];
                two[rt] = two[rt << 1] + two[rt << 1 | 1];
            }
        }
    }
    
    void update(int L, int R, int v, int l, int r, int rt) {
        if(L <= l && r <= R) {
            cnt[rt] += v;
            push_up(l, r, rt);
            return;
        }
        int m = l + r >> 1;
        if(L <= m) update(L, R, v, lson);
        if(R > m) update(L, R, v, rson);
        push_up(l, r, rt);
    }
    
    int main() {
    #ifdef LOCAL
        freopen("in.txt", "r", stdin);
    // freopen("out.txt","w",stdout);
    #endif
        ios_base::sync_with_stdio(0);
    
        int t; scanf("%d", &t);
        while(t--) {
            scanf("%d", &n);
            for(int i = 1; i <= n; ++i) {
                double x1, y1, x2, y2;
                scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
                a[i] = Seg(x1, x2, y1, 1);
                a[i + n] = Seg(x1, x2, y2, -1);
                all[i] = x1; all[i + n] = x2;
            }
            n <<= 1;
            sort(a + 1, a + 1 + n);
            sort(all + 1, all + 1 + n);
            int m = unique(all + 1, all + 1 + n) - all - 1;
    
            memset(cnt, 0, sizeof cnt);
            memset(one, 0, sizeof one);
            memset(two, 0, sizeof two);
    
            double ans = 0;
            for(int i = 1; i < n; ++i) {
                int l = lower_bound(all + 1, all + 1 + m, a[i].l) - all;
                int r = lower_bound(all + 1, all + 1 + m, a[i].r) - all;
                if(l < r) update(l, r - 1, a[i].d, 1, m, 1);
                ans += two[1] * (a[i + 1].h - a[i].h);
            }
            printf("%.2f\n", ans);
        }
        return 0;
    }
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91
       92
       93
       94
       95
       96
       97
       98
       99
       100
       101
       102
       103
       104
      
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91
       92
       93
       94
       95
       96
       97
       98
       99
       100
       101
       102
       103
       104

--------------------

# HDU 1828 \[POJ 1177\] Picture（矩形周长并） #

*  题意:
    
    > 求N<=5000个矩形的轮廓长度,也就是矩形周长并
 *  分析一:
    
    > 可以用类似矩形面积并的办法, 不过这次我们不乘高, 不算面积罢了.   
    > 需要注意的是, 由于周长的线会被重复覆盖, 我们每次需要和上一次的作差.   
    > 但是这样仅仅是x轴的, 不过我可以再y轴做一次加起来就可以了
 *  演示x轴求长度和的部分   
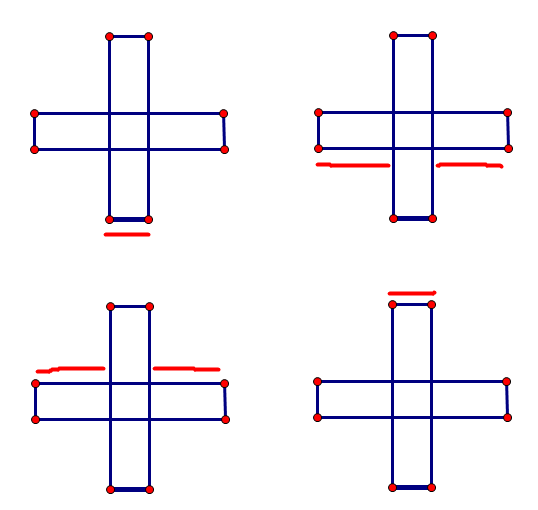
    ![这里写图片描述][20151005011720453]
 *  代码一:

//
    // Created by TaoSama on 2015-07-15
    // Copyright (c) 2015 TaoSama. All rights reserved.
    //
    //#pragma comment(linker, "/STACK:1024000000,1024000000")
    #include <algorithm>
    #include <cctype>
    #include <cmath>
    #include <cstdio>
    #include <cstdlib>
    #include <cstring>
    #include <iomanip>
    #include <iostream>
    #include <map>
    #include <queue>
    #include <string>
    #include <set>
    #include <vector>
    
    using namespace std;
    #define pr(x) cout << #x << " = " << x << " "
    #define prln(x) cout << #x << " = " << x << endl
    const int N = 1e4 + 10, INF = 0x3f3f3f3f, MOD = 1e9 + 7;
    
    int n, m[2];
    int sum[N << 2], cnt[N << 2], all[2][N];
    struct Seg {
        int l, r, h, d;
        Seg() {}
        Seg(int l, int r, int h, int d): l(l), r(r), h(h), d(d) {}
        bool operator< (const Seg& rhs) const {
       return h < rhs.h;}
    } a[2][N];
    
    #define lson l, m, rt << 1
    #define rson m + 1, r, rt << 1 | 1
    
    void push_up(int p, int l, int r, int rt) {
        if(cnt[rt]) sum[rt] = all[p][r + 1] - all[p][l];
        else if(l == r) sum[rt] = 0;
        else sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
    }
    
    void update(int p, int L, int R, int v, int l, int r, int rt) {
        if(L <= l && r <= R) {
            cnt[rt] += v;
            push_up(p, l, r, rt);
            return;
        }
    
        int m = l + r >> 1;
        if(L <= m) update(p, L, R, v, lson);
        if(R > m) update(p, L, R, v, rson);
        push_up(p, l, r, rt);
    }
    
    int main() {
    #ifdef LOCAL
        freopen("in.txt", "r", stdin);
    // freopen("out.txt","w",stdout);
    #endif
        ios_base::sync_with_stdio(0);
    
        while(scanf("%d", &n) == 1) {
            for(int i = 1; i <= n; ++i) {
                int x1, y1, x2, y2;
                scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
                all[0][i] = x1, all[0][i + n] = x2;
                all[1][i] = y1, all[1][i + n] = y2;
                a[0][i] = Seg(x1, x2, y1, 1);
                a[0][i + n] = Seg(x1, x2, y2, -1);
                a[1][i] = Seg(y1, y2, x1, 1);
                a[1][i + n] = Seg(y1, y2, x2, -1);
            }
            n <<= 1;
            sort(all[0] + 1, all[0] + 1 + n);
            m[0] = unique(all[0] + 1, all[0] + 1 + n) - all[0] - 1;
            sort(all[1] + 1, all[1] + 1 + n);
            m[1] = unique(all[1] + 1, all[1] + 1 + n) - all[1] - 1;
            sort(a[0] + 1, a[0] + 1 + n);
            sort(a[1] + 1, a[1] + 1 + n);
    
    // for(int i = 0; i < 2; ++i){ 
    // for(int j = 1; j <= m[i]; ++j) cout << all[i][j] <<' '; cout << endl;
    // } cout << endl;
    
            int ans = 0;
            for(int i = 0; i < 2; ++i) {
                int t = 0, last = 0;
                memset(cnt, 0, sizeof cnt);
                memset(sum, 0, sizeof sum);
                for(int j = 1; j <= n; ++j) {
                    int l = lower_bound(all[i] + 1, all[i] + 1 + m[i], a[i][j].l) - all[i];
                    int r = lower_bound(all[i] + 1, all[i] + 1 + m[i], a[i][j].r) - all[i];
                    if(l < r) update(i, l, r - 1, a[i][j].d, 1, m[i], 1);
                    t += abs(sum[1] - last);
                    last = sum[1];
                }
                ans += t;
            }
            printf("%d\n", ans);
        }
        return 0;
    }
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91
       92
       93
       94
       95
       96
       97
       98
       99
       100
       101
       102
       103
      
     
      
       1
       2
       3
       4
       5
       6
       7
       8
       9
       10
       11
       12
       13
       14
       15
       16
       17
       18
       19
       20
       21
       22
       23
       24
       25
       26
       27
       28
       29
       30
       31
       32
       33
       34
       35
       36
       37
       38
       39
       40
       41
       42
       43
       44
       45
       46
       47
       48
       49
       50
       51
       52
       53
       54
       55
       56
       57
       58
       59
       60
       61
       62
       63
       64
       65
       66
       67
       68
       69
       70
       71
       72
       73
       74
       75
       76
       77
       78
       79
       80
       81
       82
       83
       84
       85
       86
       87
       88
       89
       90
       91
       92
       93
       94
       95
       96
       97
       98
       99
       100
       101
       102
       103

--------------------

*  分析二:
    
    > 当然我们也可只对x轴做一次扫描线, 只要同时维护y轴竖线(就是求矩形面积并的时候的高)的个数, vtl记录竖线的个数   
    > 需要的注意的是竖线重合的情况, 需要再开变量lbd,rbd来判断重合, 避免重复计算
 *  代码二:

[20151005001227138]: /images/20220614/fc925ee4a84940a6b6d55ace9e9341e4.png
[20151005001522369]: /images/20220614/49185cc7c420417c957d00fc1786e5fb.png
[20151005001541628]: /images/20220614/abec5dda53fa412094beb52f6fe88ed4.png
[20151005001600220]: /images/20220614/8fdbc0b9f9124939b1a0efa646d4180e.png
[20151005001615715]: /images/20220614/49afbfdef4ad40f983ce1676c8625bf0.png
[20151005001627502]: /images/20220614/c837bd11486840e4b143fc76c70c2141.png
[20151005001646747]: /images/20220614/be47867061be468e9012a4ea770f82e1.png
[20151005011720453]: /images/20220614/895fef0368d04bbfbc77f91b16db30db.png