codeforces #8D Two Friends (二分答案+计算几何)-蒲公英云

题目链接;

点击打开题目链接

题意：

有两个人Alan和Bob，他们现在都在A点，现在Bob想去B点，Alan想先到C点再去B点。

要求Alan走过的长度不能超过最短路长度+t1，Bob走过的长度不能超过最短路长度+t2，求两人在一起最多走多久(分开后再汇合不算一起走)?

题解：

设Alan最多走L1，Bob最多走L2，注意还要加上t1和t2这两个差值。

首先如果Bob能陪伴Alan全程(即L2≥Distance(A,C)+Distance(C,B))，那么答案显然为min(L1,L2) 。此时他们一定是在Alan到达C之前分开的

否则两人分离时Bob一定还没有经过C点 ,这时显然不比一起回家更优。

容易发现答案是单调的，我们不妨二分答案x，即Alan 和Bob走距离为x的相同路线后分开。

不妨设分离点为P，当前二分到mid，那么：

Distance(P,A)≤mid

Distance(P,B)≤L2−mid

Distance(P,C)≤L1−Distance(B,C)−mid

即：

设分离点为P，那么点P必须满足一下三个条件：

P必须在以A为圆心半径为x的圆内，因为他们走的公共距离为x

P必须在以B为圆心半径为L2−x的圆内，为了让Bob在分开之后能及时返回B点

P必选在以C为圆心半径为L1−x−BC的圆内，因为Alan在到达C之后还要径直走回B点。

所以如果三个圆相交，那么一定存在这样的点P。

所以容易发现每个不等式中P的范围都是一个圆。

因此我们只需要判断三个圆是否有公共部分即可。

判断三个圆是否相交：

三个圆两两相交是必要条件但不是充分条件。

因为可能会有这种情况：

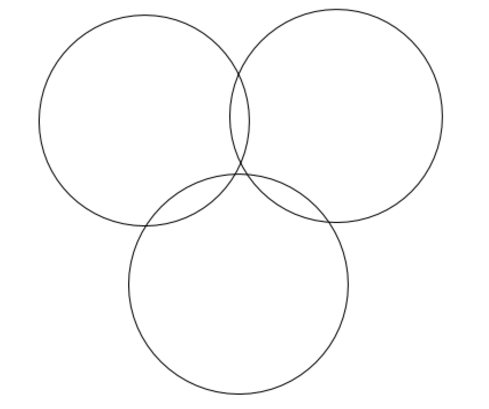
这里写图片描述

在两两相交的前提下，如果有一个小圆内含在一个大圆内的话，那么这三个圆也是相交的。

否则，如果三个圆有公共部分，两两圆必然有1∼2个交点。

如图：

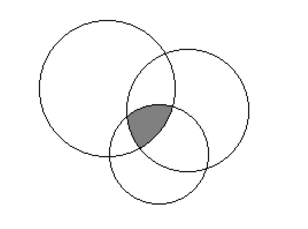
这里写图片描述

考虑这三个圆的相交区域，它必然是由若干个圆弧组成的。

所以这块区域的关键点也一定是某两个圆的交点，枚举两两圆的共三组交点，如果有一个交点满足都在三个圆的圆内或圆上，那么这三个圆就是相交的。

我的是二分了200次。
AC代码：

//#pragma comment(linker, "/STACK:102400000,102400000")
//#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <map>
#include <cmath>
#include <queue>
#include <set>
#include <bitset>
#include <iomanip>
#include <list>
#include <complex>
#include <stack>
#include <utility> 
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef vector<int> vi;
const double eps = 1e-8;  
const int INF = 1e9+7; 
const ll inf =(1LL<<62) ;
const int MOD = 1e9 + 7;  
const ll mod = (1LL<<32);
const int N =1e6+6; 
const int M=100010;
const int maxn=1001;
#define mst(a) memset(a, 0, sizeof(a))
#define M_P(x,y) make_pair(x,y)
#define pi acos(-1.0)
#define in freopen("in.txt","r",stdin) 
#define rep(i,j,k) for (int i = j; i <= k; i++)  
#define per(i,j,k) for (int i = j; i >= k; i--)  
#define lson x << 1, l, mid  
#define rson x << 1 | 1, mid + 1, r  
const int lowbit(int x) { return x&-x; }
int read(){ int v = 0, f = 1;char c =getchar();
while( c < 48 || 57 < c ){
   if(c=='-') f = -1;c = getchar();}
while(48 <= c && c <= 57) v = v*10+c-48, c = getchar();
return v*f;}
#define point complex<double>
double t1, t2;
point cinema, shop, house;
void readpoint(point &p)
{
  double x, y;
  scanf("%lf %lf", &x, &y);
  p = point(x, y);
}
bool inter(point a, double r_a, point b, double r_b, point c, double r_c) //以c为主圆求a b焦点判相交
{ 
  if (abs(c - a) <= r_a && abs(c - b) <= r_b) return true;
  b -= a; 
  c -= a; //以a为原点 
  point r = point(b.real() / abs(b), b.imag() / abs(b)); //将x轴正方向置为b
  b /= r; 
  c /= r;
  double d = (r_a * r_a - r_b * r_b + abs(b) * abs(b)) / (2 * abs(b));
  double h = sqrt(max(r_a * r_a - d * d, 0.0));
  if (abs(h * h + (d - abs(b)) * (d - abs(b))) - r_b * r_b > eps) return false;
  if (abs(point(d, h) - c) <= r_c || abs(point(d, -h) - c) <= r_c) return true;
  return false;
}
bool check(point a, double r_a, point b, double r_b, point c, double r_c) //判断三圆是否相交 
{ 
  if (r_a <= eps || r_b <= eps || r_c <= eps) return false; //有空集 
  r_a = max(r_a, 0.0); 
  r_b = max(r_b, 0.0); 
  r_c = max(r_c, 0.0);
  if (inter(a, r_a, c, r_c, b, r_b)) return true;
  if (inter(b, r_b, a, r_a, c, r_c)) return true;
  if (inter(c, r_c, b, r_b, a, r_a)) return true;
  return false;
}
int main()
{
  scanf("%lf %lf", &t1, &t2);
  readpoint(cinema); //cinema
  readpoint(house); //house
  readpoint(shop); //shop
  if (abs(shop - cinema) + abs(house - shop) <= abs(cinema - house) + t2)//Alan <= Bob + t2
  {
    printf("%lf\n", min( abs(cinema - house) + t2, abs(shop - cinema) + abs(house - shop) + t1));   
  } 
  else
  {
    double l, r, mid;
    l = 0; 
    r = min( abs(cinema - house) + t2, abs(shop - cinema) + abs(house - shop) + t1);
    for(int i=1;i<=200;i++)
    { 
      mid = (r + l) / 2;
      if (check(cinema, mid, shop, abs(shop - cinema) + t1 - mid, house, abs(house - cinema) + t2 - mid)){
        l = mid;
      } 
      else {
        r = mid;
      }
    }
    printf("%.4lf\n", l);
  }
  return 0;
}