很详细的解答tree of tree 树状DP（有图）

青旅半醒 2022-06-18 11:53 182阅读 0赞

这道题目比较有意思，而且是挺有研究一下的价值

题意：给你一棵树，每个点（树叶和结点）都有一个权值，求一拥有个K个节点的子树 的权值和最大为多少

输入： 点数n,节点数 k

输出：K个节点的子树 的最大权值

测试案例：

输入： 5 3

10 8 7 4 20  
0 1  
0 2  
1 3  
1 4  
输出： 38

下面是我的AC代码：

#include<cstdio>
    #include<cstring>
    #include<vector>
    #include<algorithm>
    using namespace std;
    
    const int maxn = 110;
    vector<int>v[maxn];
    int dp[maxn][maxn];
    int visit[maxn];
    int n,m;
    
    void DFS(int x)
    {
        visit[x]=1;
        for(int i=0;i<v[x].size();i++){
            int d=v[x][i];
            if(!visit[d]){
                DFS(d);
                for(int j=m;j>=1;j--){   //因为m的取值 至少是 1，就是结点自己本身
                    for(int k=1;k<j;k++)//至少从自身取一个结点,所以最多从 x 的子结点 d 中取 j-1个
                        dp[x][j] = max( dp[x][j], dp[x][k]+dp[d][j-k] ); //如果之前找到最大值了，那么就不会更新了
                }
            }
        }
    }
    
    int main()
    {
        while(scanf("%d%d",&n,&m)!=EOF){
            for(int i=0;i<n;i++){
    	    v[i].clear();
    	    visit[i]=0;
            }
            memset(dp,0,sizeof(dp));
            for(int i=0;i<n;i++){
                scanf("%d",&dp[i][1]);
            }
    	int a,b;
            for(int i=0;i<n-1;i++){
                scanf("%d%d",&a,&b);
                v[a].push_back(b);//添加一条边，双向关联
                v[b].push_back(a);
            }
            DFS(0);
    	int ans=0;
    	for(int i=0;i<n;i++)
    	    if(dp[i][m]>ans) ans = dp[i][m];//更新 以 每个点  为树根的k结点子树的最大值  
            printf("%d\n",ans);
        }
        return 0;
    }

1. 动态转移方程里面，因为d始终是x的子树（儿子），不会造成随便找（或者不在同一棵子树上面的情况）

2. 全局变量 dp数组，vector每次执行另外一个案例的时候，都要初始化，不然~你懂的。

3. dp\[x\]\[j\] = max( dp\[x\]\[j\], dp\[x\]\[k\]+dp\[d\]\[j-k\] ) 这一句是关键，表示以x 为根节点且节点数（包含自身）为j 的数的和的最大值，他的值会在以子树为根时进行更新。自身（不包含d儿子的其他点）取k个，从子树（d儿子）中取j-k个。

下面是我自己写的递归调用顺序，也许能够帮助理解！

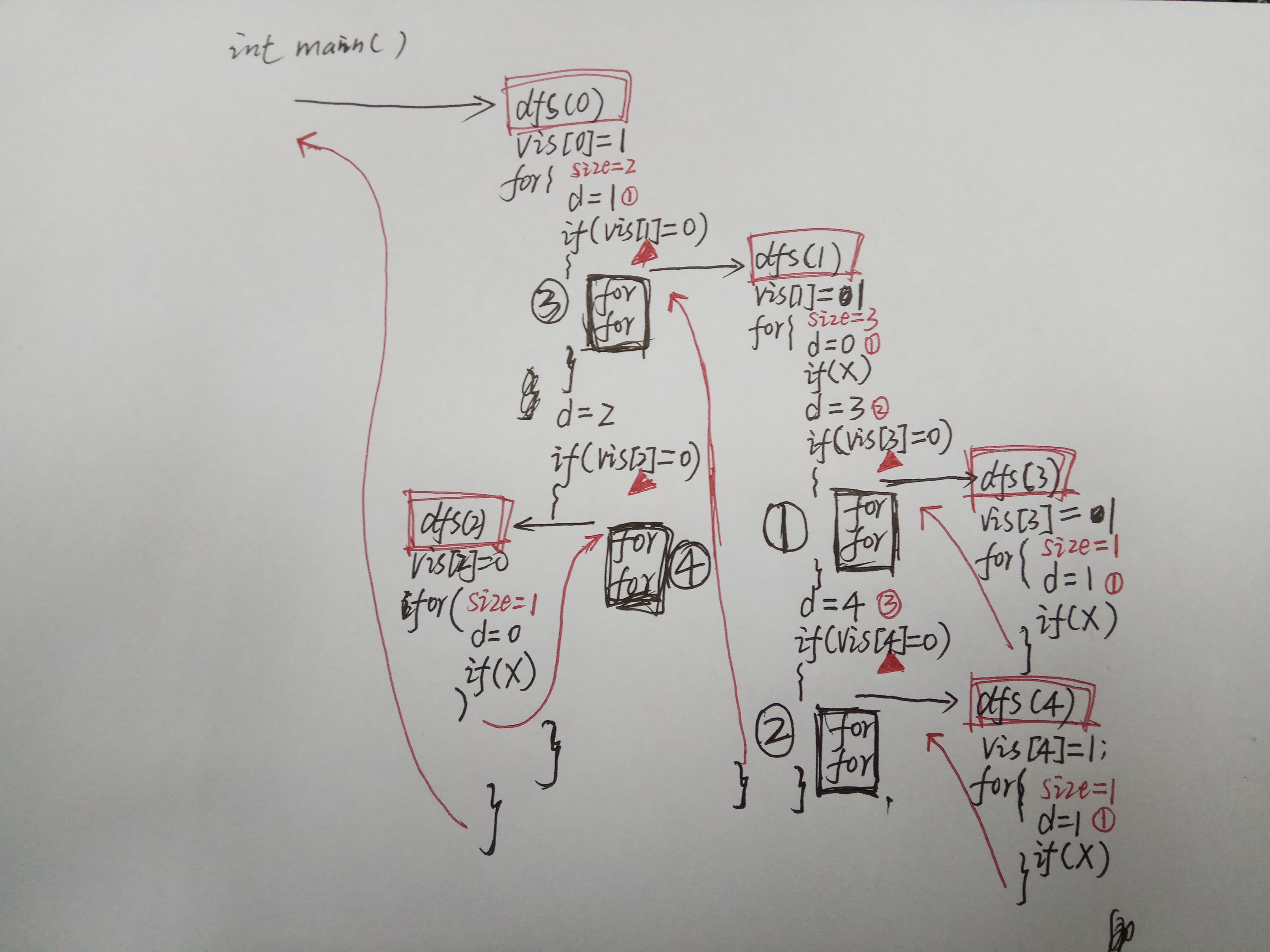
![Center][]

希望对大家有帮助！

[Center]: /images/20220618/b01d71d857b84fbebaf30962b99e058a.png