二叉树的遍历（前序遍历、中序遍历、后序遍历）-蒲公英云

二叉树

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作左子树和右子树。

树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构。

树和二叉树的2个主要差别：

树中结点的最大度数没有限制，而二叉树结点的最大度数为2；
树的结点无左、右之分，而二叉树的结点有左、右之分

二叉树也是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

(1)空二叉树无根节点的二叉树

(2)只有一个根结点的二叉树

(3)只有右子树无左子树

(4)只有左子树无右子树

(5)完全二叉树

二叉树的遍历

这里写图片描述

前序遍历

前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。
若二叉树为空则结束返回，否则：
（1）访问根结点。
（2）前序遍历左子树。
（3）前序遍历右子树。
需要注意的是：遍历左右子树时仍然采用前序遍历方法。
已知后序遍历和中序遍历，就能确定前序遍历。

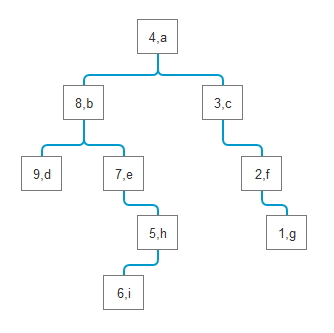
public static void beforeDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            //先遍历中间节点，再递归遍历左右   遍历顺序（中、左、右）
            System.out.println(parent);
            beforeDisplay(left);
            beforeDisplay(right);
}
上图前序遍历的结果如下：
[value: a , index: 4 ]
[value: b , index: 8 ]
[value: d , index: 9 ]
[value: e , index: 7 ]
[value: h , index: 5 ]
[value: i , index: 6 ]
[value: c , index: 3 ]
[value: f , index: 2 ]
[value: g , index: 1 ]

中序遍历

中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。
在遍历左、右子树时，仍然先遍历左子树，再访问根结点，最后遍历右子树。
即：
若二叉树为空则结束返回
否则：
（1）中序遍历左子树。
（2）访问根结点。
（3）中序遍历右子树。
需要注意的是：遍历左右子树时仍然采用中序遍历方法。
如果一棵二叉排序树的节点值是数值，中序遍历的结果为升序排列的数组。
可以利用该性质检测一棵树是否为二叉排序数。
已知前序遍历和后序遍历，不能确定唯一的中序遍历。

public static void centerDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            centerDisplay(left);
            //先遍历左节点，再递归遍历中右   遍历顺序（左、中、右）
            System.out.println(parent);
            centerDisplay(right);
}
上图中序遍历的结果如下：
[value: d , index: 9 ]
[value: b , index: 8 ]
[value: e , index: 7 ]
[value: i , index: 6 ]
[value: h , index: 5 ]
[value: a , index: 4 ]
[value: c , index: 3 ]
[value: f , index: 2 ]
[value: g , index: 1 ]

后序遍历

后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。
即：若二叉树为空则结束返回，
否则：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点
已知前序遍历和中序遍历，就能确定后序遍历。

public static void afterDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            afterDisplay(left);
            afterDisplay(right);
            //先遍历左右，后遍历中     遍历顺序（左、右、中）
            System.out.println(parent);
}
上图后序遍历的结果如下：
[value: d , index: 9 ]
[value: i , index: 6 ]
[value: h , index: 5 ]
[value: e , index: 7 ]
[value: b , index: 8 ]
[value: g , index: 1 ]
[value: f , index: 2 ]
[value: c , index: 3 ]
[value: a , index: 4 ]

以下是二叉树的结构、插入、以及遍历（完整）

public class BinaryTreeDemo {
    //二叉树结构类 
    static class Node{
        //左节点
        Node left;
        //右节点
        Node right;
        //值
        String value;
        //键
        Integer key;
        public Node getLeft() {
            return left;
        }
        public void setLeft(Node left) {
            this.left = left;
        }
        public Node getRight() {
            return right;
        }
        public void setRight(Node right) {
            this.right = right;
        }
        public Node(int key ,String value){
            this.key=key;
            this.value=value;
        }
        public Node(){
        }
        public String getValue() {
            return value;
        }
        public void setValue(String value) {
            this.value = value;
        }
        public int getKey() {
            return key;
        }
        public void setKey(int key) {
            this.key = key;
        }
        @Override
        public String toString() {
            return "[value: "+this.getValue()+" , index: "+this.getKey()+" ]";
        }
    }
    //二叉树管理类、管理节点如何分配
    static class NodeManager{
        private static Node root;
        public static void setNode(Node parent,Node node){
            //二叉树根是否是为空
            if(root==null){
                //设置第一个插入的节点为根节点
                root=node;
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            //插入的节点key 比  父节点 大   (即：大的挂左边，小的挂右边 )
            if(parent.getKey()<node.getKey()){
                //比父节点大，挂在父节点的左节点 ，前提是父节点左边无节点可比较了，否则需要递归比较
                if(left==null){
                    parent.setLeft(node);
                }else{
                    //递归左节点
                    setNode(left,node);
                }
            }else{
                if(right==null){
                    parent.setRight(node);
                }else{
                    //递归右节点
                    setNode(right,node);
                }
            }
        }
        public static void beforeDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            System.out.println(parent);
            beforeDisplay(left);
            beforeDisplay(right);
        }
        public static void centerDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            centerDisplay(left);
            System.out.println(parent);
            centerDisplay(right);
        }
        public static void afterDisplay(Node parent) {
            if(parent==null){
                return;
            }
            Node left=parent.getLeft();
            Node right=parent.getRight();
            afterDisplay(left);
            afterDisplay(right);
            System.out.println(parent);
        }
    }
    public static void main(String[] args) {
        String arr [] ={
   "a","b","c","d","e","f","g","h","i"};
        int key [] ={
   4,8,3,9,7,2,1,5,6};
        //按照数组索引顺序将键值插入到二叉树结构中
        for(int i =0 ;i<arr.length;i++){
            String c = arr[i];
            int k = key[i];
            NodeManager.setNode(NodeManager.root,new Node(k,c));
            /**
         * 第一个插入的节点  key 是4，value 是 a 
            首先二叉树需要有有根节点，第一个节点为跟节点
            第二个节点 key 是 8，value 是 b
            key比根节点大，遍历根节点的左节点，根节点的左节点为null, 所以第二节点为根节点的左节点，
            否则递归根节点的左节点的左节点，进行比较，插入节点的key比该节点的key 大挂置左边，小挂置右边（前提是左或者是右为null）以此类推。
         */
        }
        //遍历
        NodeManager.beforeDisplay(NodeManager.root);
        System.out.println("end");
        NodeManager.centerDisplay(NodeManager.root);
        System.out.println("end");
        NodeManager.afterDisplay(NodeManager.root);
        System.out.println("end");
    }
}