UFLDL教程笔记及练习答案六（稀疏编码与稀疏编码自编码表达）

稀疏编码(SparseCoding)

sparse coding也是deep learning中一个重要的分支，同样能够提取出数据集很好的特征(稀疏的)。选择使用具有稀疏性的分量来表示我们的输入数据是有原因的，因为绝大多数的感官数据，比如自然图像，可以被表示成少量基本元素的叠加，在图像中这些基本元素可以是面或者线（人脑有大量的神经元，但对于某些图像或者边缘只有很少的神经元兴奋，其他都处于抑制状态）。

稀疏编码算法的目的就是找到一组基向量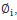使得我们能将输入向量x表示成这些基向量的线性组合：

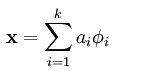
这里构成的基向量要求是超完备的，即要求k大于n，这样的方程就大多情况会有无穷多个解，此时我们给它加入一个稀疏性的限制，最终的优化公式变成了如下形式：

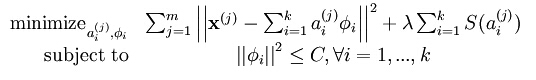
其中S(ai)就是稀疏惩罚项，可以是L0或者L1范数，L1范数和L0范数都可以表示稀疏编码，L1范数是L0范数的最优凸近似，但是L1因具有比L0更好的优化求解特性而被广泛应用。

稀疏编码自编码表达：

将稀疏编码用到深度学习中，用于提取数据集良好的稀疏特征，设A为超完备的基向量，s表示输入数据最后的稀疏特征(也就是稀疏编码中的稀疏系数),这样就可以表示成X = A*s。

其实这里的A就等同于稀疏自编码中的W2，而s就是隐层的结点值。(当具有很多样本的时候，s就是一个矩阵，每一列表示的是一个样本的稀疏特征值)

最终的优化函数变成了：

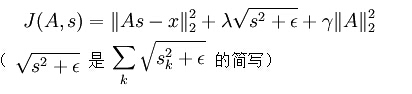
优化步骤为：

可以采用以下两个trick来提高最后的迭代速度和精度。

(1)将样本表示成良好的“迷你块”，比如你有10000个样本，我们可以每次只随机选择2000个mini_patches进行迭代，这样不仅提高了迭代的速度，也提升了收敛的速度。

(2)良好的s初始化。因为我们的目标是X=As,因此交叉迭代优化的过程中，在A给定的情况下，我们可以将s初始化为s=AT*X,但这样可能会导致稀疏性的缺失，我们在做一个规范，这里其中的s的行数就等于A列数，然后用s的每个元素除以其所在A的那一列向量的2范数。

即 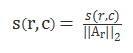其中Ar表示矩阵A的第r列。这样对s做规范化处理就是为了保持较小的稀疏惩罚值。<个人认为UFLDL教程中该处A的下标是错误的。>

因此最后的优化算法步骤表示为：

注意：以上对s和A采用交叉迭代优化，其中我们会发现分别对s和A求导的时候，发现可以直接得出A的解析形式的解，因此在优化A的时候直接给出其解析形式的解就可以了，而s我们无法给出其解析形式的解，就需要用梯度迭代等无约束的优化问题了。

测试：当有一个新的样本x，我们需要用以上训练集得到的A来优化以上cost函数得到s就是该样本的稀疏特征。这样相比之前的前馈网络的，每次对新的数据样本进行“编码”，我们必须再次执行优化过程来得到所需的系数。

注：教程中拓扑稀疏编码的内容我还没有弄明白是如何得到groupMatrix的，这里就不误导大家了。

练习答案：

以下对grad的求解可以参看这篇blog：http://www.cnblogs.com/tornadomeet/archive/2013/04/16/3024292.html给出的推导结果。

Sparse_coding_exercise.m

%% CS294A/CS294W Sparse Coding Exercise
%  Instructions
%  ------------
% 
%  This file contains code that helps you get started on the
%  sparse coding exercise. In this exercise, you will need to modify
%  sparseCodingFeatureCost.m and sparseCodingWeightCost.m. You will also
%  need to modify this file, sparseCodingExercise.m slightly.
% Add the paths to your earlier exercises if necessary
% addpath /path/to/solution
%%======================================================================
%% STEP 0: Initialization
%  Here we initialize some parameters used for the exercise.
numPatches = 20000;   % number of patches
numFeatures = 121;    % number of features to learn
patchDim = 8;         % patch dimension
visibleSize = patchDim * patchDim; 
% dimension of the grouping region (poolDim x poolDim) for topographic sparse coding
poolDim = 3;
% number of patches per batch
batchNumPatches = 2000; 
lambda = 5e-5;  % L1-regularisation parameter (on features)
epsilon = 1e-5; % L1-regularisation epsilon |x| ~ sqrt(x^2 + epsilon)
gamma = 1e-2;   % L2-regularisation parameter (on basis)
%%======================================================================
%% STEP 1: Sample patches
images = load('IMAGES.mat');
images = images.IMAGES;
patches = sampleIMAGES(images, patchDim, numPatches);
display_network(patches(:, 1:64));
%%======================================================================
%% STEP 2: Implement and check sparse coding cost functions
%  Implement the two sparse coding cost functions and check your gradients.
%  The two cost functions are
%  1) sparseCodingFeatureCost (in sparseCodingFeatureCost.m) for the features 
%     (used when optimizing for s, which is called featureMatrix in this exercise) 
%  2) sparseCodingWeightCost (in sparseCodingWeightCost.m) for the weights
%     (used when optimizing for A, which is called weightMatrix in this exericse)
% We reduce the number of features and number of patches for debugging
% numFeatures = 25;
% patches = patches(:, 1:5);
% numPatches = 5;
weightMatrix = randn(visibleSize, numFeatures) * 0.005;
featureMatrix = randn(numFeatures, numPatches) * 0.005;
%% STEP 2a: Implement and test weight cost
%  Implement sparseCodingWeightCost in sparseCodingWeightCost.m and check
%  the gradient
[cost, grad] = sparseCodingWeightCost(weightMatrix, featureMatrix, visibleSize, numFeatures, patches, gamma, lambda, epsilon);
numgrad = computeNumericalGradient( @(x) sparseCodingWeightCost(x, featureMatrix, visibleSize, numFeatures, patches, gamma, lambda, epsilon), weightMatrix(:) );
% Uncomment the blow line to display the numerical and analytic gradients side by side
% disp([numgrad grad]);     
diff = norm(numgrad-grad)/norm(numgrad+grad);
fprintf('Weight difference: %g\n', diff);
assert(diff < 1e-8, 'Weight difference too large. Check your weight cost function. ');
%% STEP 2b: Implement and test feature cost (non-topographic)
%  Implement sparseCodingFeatureCost in sparseCodingFeatureCost.m and check
%  the gradient. You may wish to implement the non-topographic version of
%  the cost function first, and extend it to the topographic version later.
% Set epsilon to a larger value so checking the gradient numerically makes sense
epsilon = 1e-2;
% We pass in the identity matrix as the grouping matrix, putting each
% feature in a group on its own.
groupMatrix = eye(numFeatures);
[cost, grad] = sparseCodingFeatureCost(weightMatrix, featureMatrix, visibleSize, numFeatures, patches, gamma, lambda, epsilon, groupMatrix);
numgrad = computeNumericalGradient( @(x) sparseCodingFeatureCost(weightMatrix, x, visibleSize, numFeatures, patches, gamma, lambda, epsilon, groupMatrix), featureMatrix(:) );
% Uncomment the blow line to display the numerical and analytic gradients side by side
% disp([numgrad grad]); 
diff = norm(numgrad-grad)/norm(numgrad+grad);
fprintf('Feature difference (non-topographic): %g\n', diff);
assert(diff < 1e-8, 'Feature difference too large. Check your feature cost function. ');
%% STEP 2c: Implement and test feature cost (topographic)
%  Implement sparseCodingFeatureCost in sparseCodingFeatureCost.m and check
%  the gradient. This time, we will pass a random grouping matrix in to
%  check if your costs and gradients are correct for the topographic
%  version.
% Set epsilon to a larger value so checking the gradient numerically makes sense
epsilon = 1e-2;
% This time we pass in a random grouping matrix to check if the grouping is
% correct.
groupMatrix = rand(100, numFeatures);
[cost, grad] = sparseCodingFeatureCost(weightMatrix, featureMatrix, visibleSize, numFeatures, patches, gamma, lambda, epsilon, groupMatrix);
numgrad = computeNumericalGradient( @(x) sparseCodingFeatureCost(weightMatrix, x, visibleSize, numFeatures, patches, gamma, lambda, epsilon, groupMatrix), featureMatrix(:) );
% Uncomment the blow line to display the numerical and analytic gradients side by side
% disp([numgrad grad]); 
diff = norm(numgrad-grad)/norm(numgrad+grad);
fprintf('Feature difference (topographic): %g\n', diff);
assert(diff < 1e-8, 'Feature difference too large. Check your feature cost function. ');
%%======================================================================
%% STEP 3: Iterative optimization
%  Once you have implemented the cost functions, you can now optimize for
%  the objective iteratively. The code to do the iterative optimization 
%  using mini-batching and good initialization of the features has already
%  been included for you. 
% 
%  However, you will still need to derive and fill in the analytic solution 
%  for optimizing the weight matrix given the features. 
%  Derive the solution and implement it in the code below, verify the
%  gradient as described in the instructions below, and then run the
%  iterative optimization.
% Initialize options for minFunc
options.Method = 'lbfgs';
options.display = 'off';
options.verbose = 0;
% Initialize matrices
weightMatrix = rand(visibleSize, numFeatures);
featureMatrix = rand(numFeatures, batchNumPatches);
% Initialize grouping matrix
assert(floor(sqrt(numFeatures)) ^2 == numFeatures, 'numFeatures should be a perfect square');
donutDim = floor(sqrt(numFeatures));
assert(donutDim * donutDim == numFeatures,'donutDim^2 must be equal to numFeatures');
groupMatrix = zeros(numFeatures, donutDim, donutDim);
groupNum = 1;     %% 获得拓扑稀疏编码   这段处理不太懂啊！！
for row = 1:donutDim
    for col = 1:donutDim
        groupMatrix(groupNum, 1:poolDim, 1:poolDim) = 1;
        groupNum = groupNum + 1;
        groupMatrix = circshift(groupMatrix, [0 0 -1]);
    end
    groupMatrix = circshift(groupMatrix, [0 -1, 0]);
end
groupMatrix = reshape(groupMatrix, numFeatures, numFeatures);
if isequal(questdlg('Initialize grouping matrix for topographic or non-topographic sparse coding?', 'Topographic/non-topographic?', 'Non-topographic', 'Topographic', 'Non-topographic'), 'Non-topographic')
    groupMatrix = eye(numFeatures);
end
% Initial batch
indices = randperm(numPatches);
indices = indices(1:batchNumPatches);
batchPatches = patches(:, indices);                           
fprintf('%6s%12s%12s%12s%12s\n','Iter', 'fObj','fResidue','fSparsity','fWeight');
for iteration = 1:200                                 %% 因为要交替优化直到最小化cost function, 所以才这样进行的
    error = weightMatrix * featureMatrix - batchPatches;
    error = sum(error(:) .^ 2) / batchNumPatches;
    fResidue = error;
    R = groupMatrix * (featureMatrix .^ 2);
    R = sqrt(R + epsilon);    
    fSparsity = lambda * sum(R(:));    
    fWeight = gamma * sum(weightMatrix(:) .^ 2);
    fprintf('  %4d  %10.4f  %10.4f  %10.4f  %10.4f\n', iteration, fResidue+fSparsity+fWeight, fResidue, fSparsity, fWeight)   %% 以上这部分可以不用的，只是为了显示最终的
    % Select a new batch
    indices = randperm(numPatches);   %% 重新挑选2000个样本用来进行训练
    indices = indices(1:batchNumPatches);
    batchPatches = patches(:, indices);         %%% 重新挑选的样本                 
    % Reinitialize featureMatrix with respect to the new batch
    featureMatrix = weightMatrix' * batchPatches;           %% trick 对featureMatrix(s)进行初始化 --技巧 方法
    normWM = sum(weightMatrix .^ 2)';                     %%%%% 也就是weightMatrix矩阵每列的平方和
    featureMatrix = bsxfun(@rdivide, featureMatrix, normWM);   %% featureMatrix除以上者
    % Optimize for feature matrix    
    options.maxIter = 20;   % 迭代20次，并对featureMatrix进行无约束优化
    [featureMatrix, cost] = minFunc( @(x) sparseCodingFeatureCost(weightMatrix, x, visibleSize, numFeatures, batchPatches, gamma, lambda, epsilon, groupMatrix), ...
                                           featureMatrix(:), options);
    featureMatrix = reshape(featureMatrix, numFeatures, batchNumPatches);                                      
    % Optimize for weight matrix  
    weightMatrix = zeros(visibleSize, numFeatures);      %%%  通过直接求导得出对weightMatrix进行优化，这里无需进行梯度迭代或者牛顿法等得出最终的结果
    weightMatrix = batchPatches*featureMatrix'/(gamma*batchNumPatches* eye(size(featureMatrix, 1)) + featureMatrix*featureMatrix');
    % -------------------- YOUR CODE HERE --------------------
    % Instructions:
    %   Fill in the analytic solution for weightMatrix that minimizes 
    %   the weight cost here.     
    %   Once that is done, use the code provided below to check that your
    %   closed form solution is correct.
    %   Once you have verified that your closed form solution is correct,
    %   you should comment out the checking code before running the
    %   optimization.
    [cost, grad] = sparseCodingWeightCost(weightMatrix, featureMatrix, visibleSize, numFeatures, batchPatches, gamma, lambda, epsilon, groupMatrix);
    assert(norm(grad) < 1e-12, 'Weight gradient should be close to 0. Check your closed form solution for weightMatrix again.')
    error('Weight gradient is okay. Comment out checking code before running optimization.');
    % -------------------- YOUR CODE HERE --------------------  
    % Visualize learned basis
    figure(1);
    display_network(weightMatrix);           
end

sparseCodingWeight.m

function [cost, grad] = sparseCodingWeightCost(weightMatrix, featureMatrix, visibleSize, numFeatures,  patches, gamma, lambda, epsilon, groupMatrix)
%sparseCodingWeightCost - given the features in featureMatrix, 
%                         computes the cost and gradient with respect to
%                         the weights, given in weightMatrix
% parameters
%   weightMatrix  - the weight matrix. weightMatrix(:, c) is the cth basis
%                   vector.
%   featureMatrix - the feature matrix. featureMatrix(:, c) is the features
%                   for the cth example
%   visibleSize   - number of pixels in the patches
%   numFeatures   - number of features
%   patches       - patches
%   gamma         - weight decay parameter (on weightMatrix)
%   lambda        - L1 sparsity weight (on featureMatrix)
%   epsilon       - L1 sparsity epsilon
%   groupMatrix   - the grouping matrix. groupMatrix(r, :) indicates the
%                   features included in the rth group. groupMatrix(r, c)
%                   is 1 if the cth feature is in the rth group and 0
%                   otherwise.
    if exist('groupMatrix', 'var')
        assert(size(groupMatrix, 2) == numFeatures, 'groupMatrix has bad dimension');
    else
        groupMatrix = eye(numFeatures);
    end
    numExamples = size(patches, 2);
    weightMatrix = reshape(weightMatrix, visibleSize, numFeatures);
    featureMatrix = reshape(featureMatrix, numFeatures, numExamples);
    % -------------------- YOUR CODE HERE --------------------
    % Instructions:
    %   Write code to compute the cost and gradient with respect to the
    %   weights given in weightMatrix.     
    % -------------------- YOUR CODE HERE --------------------   
    ave_square = sum(sum((weightMatrix * featureMatrix - patches).^2))./numExamples;   %计算重构误差
    weight_decay = gamma * sum(sum(weightMatrix.^2));            %
    cost = ave_square + weight_decay;
    grad = (2*weightMatrix*featureMatrix*featureMatrix' - 2 * patches*featureMatrix')./numExamples + 2*gamma*weightMatrix;
    grad = grad(:);
end

sparseCodingFeatureCost.m

function [cost, grad] = sparseCodingFeatureCost(weightMatrix, featureMatrix, visibleSize, numFeatures, patches, gamma, lambda, epsilon, groupMatrix)
%sparseCodingFeatureCost - given the weights in weightMatrix,
%                          computes the cost and gradient with respect to
%                          the features, given in featureMatrix
% parameters
%   weightMatrix  - the weight matrix. weightMatrix(:, c) is the cth basis
%                   vector.
%   featureMatrix - the feature matrix. featureMatrix(:, c) is the features
%                   for the cth example
%   visibleSize   - number of pixels in the patches
%   numFeatures   - number of features
%   patches       - patches
%   gamma         - weight decay parameter (on weightMatrix)
%   lambda        - L1 sparsity weight (on featureMatrix)
%   epsilon       - L1 sparsity epsilon
%   groupMatrix   - the grouping matrix. groupMatrix(r, :) indicates the
%                   features included in the rth group. groupMatrix(r, c)
%                   is 1 if the cth feature is in the rth group and 0
%                   otherwise.
    isTopo = 1;
    if exist('groupMatrix', 'var')
        assert(size(groupMatrix, 2) == numFeatures, 'groupMatrix has bad dimension');
        if(isequal(groupMatrix, eye(numFeatures)))
            isTopo = 0;
        end
    else
        groupMatrix = eye(numFeatures);
        isTopo = 0;
    end
    numExamples = size(patches, 2);
    weightMatrix = reshape(weightMatrix, visibleSize, numFeatures);
    featureMatrix = reshape(featureMatrix, numFeatures, numExamples);
    % -------------------- YOUR CODE HERE --------------------
    % Instructions:
    %   Write code to compute the cost and gradient with respect to the
    %   features given in featureMatrix.     
    %   You may wish to write the non-topographic version, ignoring
    %   the grouping matrix groupMatrix first, and extend the 
    %   non-topographic version to the topographic version later.
    % -------------------- YOUR CODE HERE --------------------
     ave_square = sum(sum((weightMatrix * featureMatrix - patches).^2))./numExamples;    % 计算重构误差
     sparsity = lambda .* sum(sum(sqrt( groupMatrix * (featureMatrix.^2) + epsilon)));      %计算系数惩罚项
     cost = ave_square + sparsity;
     gradResidue = (2* weightMatrix'* weightMatrix*featureMatrix - 2*weightMatrix'*patches)./numExamples; %%+ lambda*featureMatrix./sqrt(featureMatrix.^2+epsilon);
     if ~isTopo
        gradSparsity = lambda*featureMatrix./sqrt(featureMatrix.^2+epsilon);   %%% 不是拓扑的稀疏编码
     else
        gradSparsity = lambda * groupMatrix'*(groupMatrix *(featureMatrix .^ 2) + epsilon).^(0.5).*featureMatrix;   %% 拓扑稀疏编码
     end
     grad = gradResidue + gradSparsity;
     grad = grad(:);
end

参考文献：

1：UFLDL教程http://ufldl.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B

2：http://blog.csdn.net/zouxy09/article/details/24971995/机器学习中的范数规则化之（一）L0、L1与L2范数

3：http://www.cnblogs.com/tornadomeet/archive/2013/04/16/3024292.htmlDeep learning：二十九(Sparse coding练习)

4：http://www.cnblogs.com/tornadomeet/archive/2013/04/13/3018393.htmlDeep learning：二十六(Sparse coding简单理解)