http://[blog.csdn.net/pipisorry/article/details/46383947][blog.csdn.net_pipisorry_article_details_46383947]

编辑距离Edit distance/Levenshtein distance-序列之间的距离

X 和Y 的编辑距离定义为：从字符串strings X转换到 Y 需要的插入、删除、替换两个相邻的基本单位(字符)的最小个数。

给定 2 个字符串 a, b. 编辑距离是将 a 转换为 b 的最少操作次数，操作只允许如下 3 种：

插入一个字符，例如：fj -> fxj
删除一个字符，例如：fxj -> fj
替换一个字符，例如：fxj -> fyj

如：
ed (recoginze, recognize) = 1
ed (sailn, failing) = 3

编辑距离是一个动态规划的问题。

编辑距离常用在英语单词拼写检查中，可以使用有限自动机实现[宗成庆:《自然语言处理》讲义：第03章形式语言与自动机及其在自然语言处理中的应用NLP-03+FL_and_ItsApp.pdf]。

编辑距离与最长公共子序列LCS

Center
子串的定义：one string is a sub-sequence of another if we can get the first by deleting 0 or more positions from the second.the positions of the deleted characters did not have to be consecutive.
计算x,y编辑距离的两种方式
Center 1

第一种方式中我们可以逆向编辑：we can get from y to x by doing the same edits in reverse.delete u and v,and then we insert a to get x.

[海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记之局部敏感哈希LSH的距离度量方法]

Note: lz代码证明了，并没有这种关系，这里只是一个特例碰巧而已，不知道是不是lcs定义不同还是怎么回事。如”bedaacbade”和 “dccaeedbeb”的lcs为5，而编辑距离为10，并没有以上关系。

扩展的编辑距离(Damerau-Levenshtein Distance)

扩展的编辑距离在思想上与编辑距离一样，只是除插入、删除和替换操作外，还支持 相邻字符的交换 这样一个操作，增加这个操作的考虑是人们在计算机上输入文档时的错误情况中，因为快速敲击而前后两个字符的顺序被输错的情况很常见。

皮皮blog

编辑距离的动态规划解

思路

用分治的思想解决比较简单，将复杂的问题分解成相似的子问题。

假设字符串 a, 共 m 位，从 a[1] 到 a[m]，字符串 b, 共 n 位，从 b[1] 到 b[n]
d[i][j] 表示字符串 a[1]-a[i] 转换为 b[1]-b[j] 的编辑距离。

那么有如下递归规律（a[i] 和 b[j] 分别是当前要计算编辑距离的子字符串 a 和 b 的最后一位）：

当 a[i] 等于 b[j] 时，d[i][j] = d[i-1][j-1], 比如 fxy -> fay 的编辑距离等于 fx -> fa 的编辑距离
当 a[i] 不等于 b[j] 时，d[i][j] 等于如下 3 项的最小值：
- d[i-1][j] + 1（删除 a[i]（删除等价于插入操作，相当于插入b中插入a[i[）），比如 fxy -> fab 的编辑距离 = fx -> fab 的编辑距离 + 1
- d[i][j-1] + 1（删除 b[j]或者插入b[j])，比如 fxy -> fab 的编辑距离 = fxyb -> fab 的编辑距离 + 1 = fxy -> fa 的编辑距离 + 1
- d[i-1][j-1] + 1（将a[i]b[j]同时删除（等价于交换操作）），比如 fxy -> fab 的编辑距离 = fxb -> fab 的编辑距离 + 1 = fx -> fa 的编辑距离 + 1

递归边界：

a[i][0] = i, b 字符串为空，表示将 a[1]-a[i] 全部删除，所以编辑距离为 i
a[0][j] = j, a 字符串为空，表示 a 插入 b[1]-b[j]，所以编辑距离为 j

递归思路代码

按照上面的思路将代码写下来

int edit_distance(char *a, char *b, int i, int j)
{
    if (j == 0) {
        return i;
    } else if (i == 0) {
        return j;
    // 算法中 a, b 字符串下标从 1 开始，c 语言从 0 开始，所以 -1
    } else if (a[i-1] == b[j-1]) {
        return edit_distance(a, b, i - 1, j - 1);
    } else {
        return min_of_three(edit_distance(a, b, i - 1, j) + 1,
                            edit_distance(a, b, i, j - 1) + 1,
                            edit_distance(a, b, i - 1, j - 1) + 1);
    }
}
edit_distance(stra, strb, strlen(stra), strlen(strb));

但是这个代码的性能很低下，时间复杂度是指数增长的，很多相同的子问题其实是经过了多次求解。

解决这类问题的办法是1 使用记忆

ins = dict()
def edit_distance(w1, w2, i, j):
    if (i, j) in ins:
        return ins[(i, j)]
    if len(w1) <= i:
        return len(w2) - j
    if len(w2) <= j:
        return len(w1) - i
    if w1[i] == w2[j]:
        minl = edit_distance(w1, w2, i + 1, j + 1)
    else:
        minl = min(edit_distance(w1, w2, i + 1, j + 1), edit_distance(w1, w2, i, j + 1)
                   , edit_distance(w1, w2, i + 1, j)) + 1
    ins[(i, j)] = minl
    return minl

2 使用动态规划。

用动态规划思想优化时间复杂度

以上解决思路是从后往前算的，想知道 edit_distance(a, b, i, j) 就需要知道 edit_distance(a, b, i-1, j-1)。
如果从前往后算，先算出各个子问题，然后根据子问题，计算出原问题。

例如以字符串 a = “ace”, b = “abcdef” 为例：

首先建立一个矩阵，用来存放子问题及原问题的编辑距离，并将递归边界在矩阵中填好，如下：

	0	a	b	c	d	e	f
0	0	1	2	3	4	5	6
a	1
c	2
e	3

然后计算 i = 1, j = 1 所对应的编辑距离：比较 a[i] 和 b[j] 是否相等然后根据递归规律算出这个值
比如在这种情况下 a[i] = a 和 b[j] = a, 那么 d[i][j] 就等于 d[i-1][j-1] 等于 0
然后计算 i = 1, j = 2 直到算出 i = 3, j = 6, 原问题的编辑距离就等于 d[3][6]
最终矩阵如下：

	0	a	b	c	d	e	f
0	0	1	2	3	4	5	6
a	1	0	1	2	3	4	5
c	2	1	1	1	2	3	4
e	3	2	2	2	2	2	3

即要计算d[i][j]只需要知道3个位置上的值。

代码如下：

int edit_distance(char *a, char *b){
    int lena = strlen(a);
    int lenb = strlen(b);
    int d[lena+1][lenb+1];
    int i, j;
    for (i = 0; i <= lena; i++) {
        d[i][0] = i;
    }
    for (j = 0; j <= lenb; j++) {
        d[0][j] = j;
    }
    for (i = 1; i <= lena; i++) {
        for (j = 1; j <= lenb; j++) {
            // 算法中 a, b 字符串下标从 1 开始，c 语言从 0 开始，所以 -1
            if (a[i-1] == b[j-1]) {
                d[i][j] = d[i-1][j-1];
            } else {
                d[i][j] = min_of_three(d[i-1][j]+1, d[i][j-1]+1, d[i-1][j-1]+1);
            }
        }
    }
    return d[lena][lenb];
}
def edit_distance(w1, w2):
    len1 = len(w1)
    len2 = len(w2)
    matrix = [[0 for _ in range(len2 + 1)] for _ in range(len1 + 1)]
    for j in range(len2):
        matrix[0][j + 1] = j + 1
    for i in range(len1):
        matrix[i + 1][0] = i + 1
    for i in range(1, len1 + 1):
        for j in range(1, len2 + 1):
            if w1[i - 1] == w2[j - 1]:
                matrix[i][j] = matrix[i - 1][j - 1]
            else:
                matrix[i][j] = min(matrix[i - 1][j], matrix[i - 1][j - 1], matrix[i][j - 1]) + 1
    return matrix[len1][len2]

这个算法的时间复杂度为O(mn)。

空间复杂度为 O(mn)，空间复杂度可以继续优化，因为计算矩阵某位置值的时候总是需要有限的量，同一时间并不需要所有矩阵的值。

根据具体问题优化空间复杂度

还是以 a = “fxy”, b = “fab” 为例，例如计算 d[1][3], 也就是下图中的绿色方块，我们需要知道的值只需 3 个，下图中蓝色方块的值

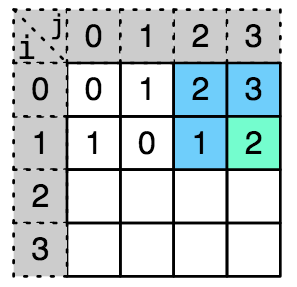
进一步分析，我们知道，当计算 d[1] 这行的时候，我们只需知道 d[0] 这行的值，同理我们计算当前行的时候只需知道上一行就可以了。
再进一步分析，其实我们只需要一行就可以了，每次计算的时候我们需要的 3 个值，其中上边和左边的值我们可以直接得到，坐上角的值需要临时变量（如下代码使用 old）来记录。

代码如下：

int edit_distance(char *a, char *b){
    int lena = strlen(a);
    int lenb = strlen(b);
    int d[lenb+1];
    int i, j, old, tnmp;
    for (j = 0; j <= lenb; j++) {
        d[j] = j;
    }
    for (i = 1; i <= lena; i++) {
        old = i - 1;
        d[0] = i;
        for (j = 1; j <= lenb; j++) {
            temp = d[j];
            // 算法中 a, b 字符串下标从 1 开始，c 语言从 0 开始，所以 -1
            if (a[i-1] == b[j-1]) {
                d[j] = old;
            } else {
                d[j] = min_of_three(d[j] + 1, d[j-1] + 1, old + 1);
            }
            old = temp;
        }
    }
    return d[lenb];
}

写代码的过程中需要注意的一点就是，当一行计算好之后开始下一行的时候，要初始化 old 和 d[0] 的值

优化过后时间复杂度还是 O(mn), 空间复杂度 O(min(m,n))。

皮皮blog

DTW 距离（Dynamic Time Warp）

时间序列是序列之间距离的另外一个例子。DTW 距离（Dynamic Time Warp）是序列信号在时间或者速度上不匹配的时候一种衡量相似度的方法。举个例子，两份原本一样声音样本A、B都说了“你好”，A在时间上发生了扭曲，“你”这个音延长了几秒。最后A:“你~~好”，B：“你好”。DTW正是这样一种可以用来匹配A、B之间的最短距离的算法。DTW 距离在保持信号先后顺序的限制下对时间信号进行“膨胀”或者“收缩”，找到最优的匹配，与编辑距离相似，这其实也是一个动态规划的问题。

实现代码

import sys
distance = lambda a,b : 0 if a==b else 1
def dtw(sa,sb):
    '''
    >>>dtw(u"干啦今今今今今天天气气气气气好好好好啊啊啊", u"今天天气好好啊")
    2
    '''
    MAX_COST = 1<<32
    #初始化一个len(sb) 行(i)，len(sa)列(j)的二维矩阵
    len_sa = len(sa)
    len_sb = len(sb)
    # BUG:这样是错误的(浅拷贝): dtw_array = [[MAX_COST]*len(sa)]*len(sb)
    dtw_array = [[MAX_COST for i in range(len_sa)] for j in range(len_sb)]
    dtw_array[0][0] = distance(sa[0],sb[0])
    for i in xrange(0, len_sb):
        for j in xrange(0, len_sa):
            if i+j==0:
                continue
            nb = []
            if i > 0: nb.append(dtw_array[i-1][j])
            if j > 0: nb.append(dtw_array[i][j-1])
            if i > 0 and j > 0: nb.append(dtw_array[i-1][j-1])
            min_route = min(nb)
            cost = distance(sa[j],sb[i])
            dtw_array[i][j] = cost + min_route
    return dtw_array[len_sb-1][len_sa-1]
def main(argv):
    s1 = u'干啦今今今今今天天气气气气气好好好好啊啊啊'
    s2 = u'今天天气好好啊'
    d = dtw(s1, s2)
    print d
    return 0
if __name__ == '__main__':
    sys.exit(main(sys.argv))