最长不下降自序列（最长递增子序列）C++动态规划-蒲公英云

最长不下降自序列（最长递增子序列）C++动态规划

你的名字 2022-08-29 15:52 281阅读 0赞

题目：http://www.kencoding.net/problem.php?id=1112

最长递增子序列（Longest Increasing Subsequence , LIS）问题：给定一个长度为N的数组，找出一个最长的单调递增子序列。例如一个长度为7的序列 A = 5 , 6 , 7 , 4 , 2 , 8 , 3 A={5,6,7,4,2,8,3} A=5,6,7,4,2,8,3，它最长的单调递增子序列为 5 , 6 , 7 , 8 {5,6,7,8} 5,6,7,8，长度为4.

在这里插入图片描述

此题答案，也是最长不下降自序列的固定模板：

#include <cstdio>
int a[1000];
int n;
int f[1000];
int main(){ 
    scanf("%d",&n);
    int i;
    int j;
    for (i=1;i<=n;i++){ 
        scanf("%d",&a[i]);
    }
    //每个点的f值不可能小于1
    for(i=1;i<=n;i++) f[i] =1;
    int max = 1;
    for (i=2;i<=n;i++){ 
        for(j=1;j<i;j++){ 
            if( a[j] <= a[i] && f[i] < f[j]+1){ 
                f[i] = f[j]+1;
                if(max < f[i])
                    max = f[i];
            }
        }
    }
    printf("%d",max);
    return 0;
}

下面给出一个例题

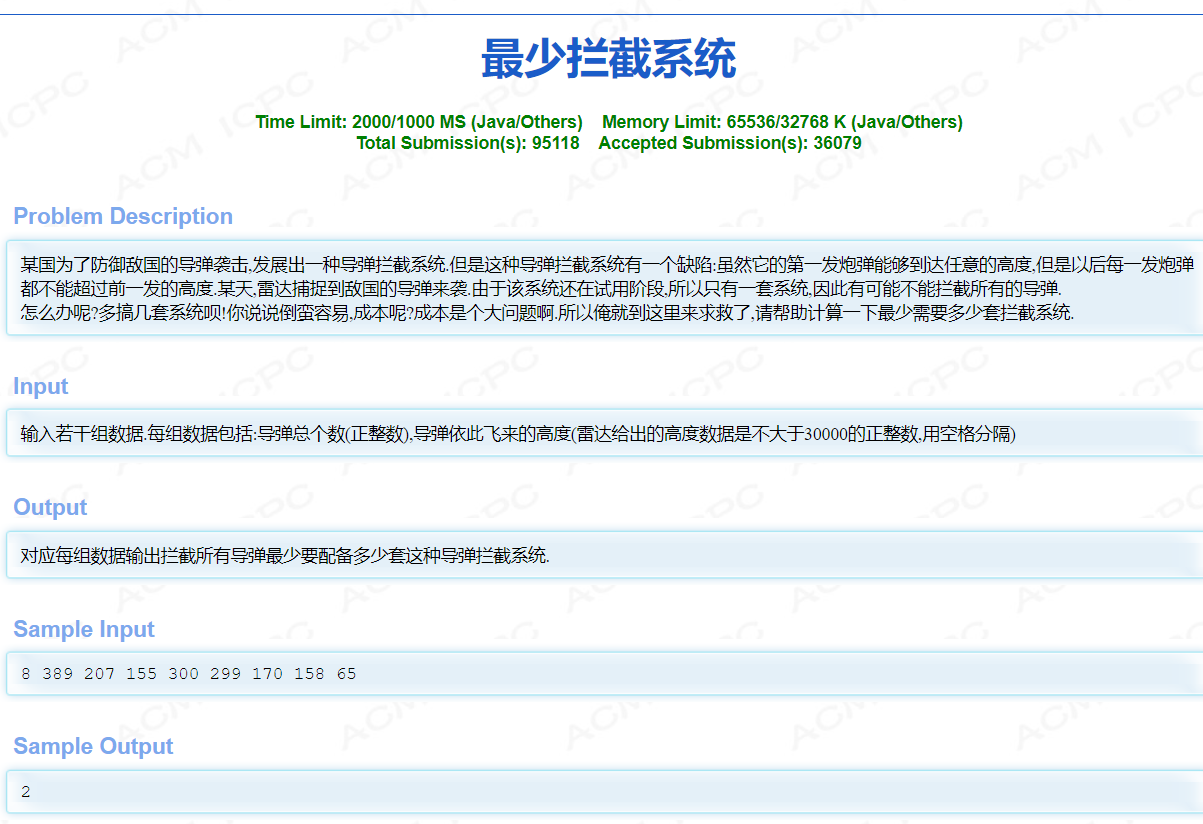
导弹拦截系统 hdu 1257

某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统.但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能超过前一发的高度.某天,雷达捕捉到敌国的导弹来袭.由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹.
怎么办呢?多搞几套系统呗!你说说倒蛮容易,成本呢?成本是个大问题啊.所以俺就到这里来求救了,请帮助计算一下最少需要多少套拦截系统.

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100010;
int n, high[MAXN];
int LIS(){ 
    int ans = 1;
    int dp[MAXN];
    dp[1] = 1;
    for (int i = 2; i <= n; i++)
    { 
        int max= 0;
        for (int j = 1; j < i; j++)
        { 
            if (dp[j] > max && high[j] < high[i])
                max = dp[j];
        }
        dp[i] = max + 1;
        if (dp[i] > ans)
            ans = dp[i];
    }
    return ans;
}
int main(){ 
    while (cin >> n)
    { 
        for (int i = 1; i <= n; i++)
        { 
            cin >> high[i];
        }
        cout << LIS() << endl;
    }
}