565 数组嵌套（图论思想-求解所有环的最大长度）-蒲公英云

565 数组嵌套（图论思想-求解所有环的最大长度）

1. 问题描述：

索引从0开始长度为N的数组A，包含0到N - 1的所有整数。找到最大的集合S并返回其大小，其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], … }且遵守以下的规则。假设选择索引为i的元素A[i]为S的第一个元素，S的下一个元素应该是A[A[i]]，之后是A[A[A[i]]]… 以此类推，不断添加直到S出现重复的元素。

示例 1:

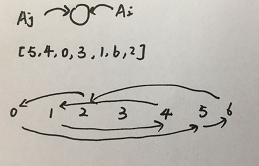
输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}

提示：

N是[1, 20,000]之间的整数。
A中不含有重复的元素。
A中的元素大小在[0, N-1]之间。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/array-nesting

2. 思路分析：

首先需要理解题目的意思，我们可以先画一下图，可以发现抽象出来是一个图论的问题（题目中蕴含了图论的思想）。我们可以将数组中的每一个位置看成是图中的点，数组中的元素值表示当前位置对应的点到另外一个点存在联系，那么将这两个位置连一条边，并且每个点只有一条出边，因为A数组中的元素值为0~N-1，所以对于每个点也只有一条入边，所以对于图中每一个点都是入度 = 出度 = 1，而满足这种性质的一定是由若干个环组成的图，对于每一个集合对应着一个环，所以本质上求解的是所有环的最大长度。对于这道题目来说因为只有N条边，所以我们可以从前遍历当发现当前这个位置之前没有被遍历过说明是新的环的起点那么从当前位置开始遍历找到当前起点构成的整个环（当前位置被遍历过之后那么标记为-1），在求解环的长度的时候维护环的最大长度即可，最终每一个点只被遍历一次。

3. 代码如下：

from typing import List
class Solution:
    def arrayNesting(self, nums: List[int]) -> int:
        res = 0
        for i in range(len(nums)):
            # s记录当前环的长度
            s = 0
            j = i
            # 找到了新的环的起点
            if nums[i] != -1:
                while nums[j] != -1:
                    # next为环的下一个位置
                    next = nums[j]
                    s += 1
                    # 当前位置被遍历过那么标记为-1
                    nums[j] = -1
                    j = next
                res = max(res, s)
        return res