财商训练(01)————等额本息和等额本金房贷的区别-蒲公英云

财商训练(01)————等额本息和等额本金房贷的区别

文章目录

- - 01 等额本息
  - - 每月还款数额计算公式
    - 案例分析：
  - 02 等额本金
  - - 每月还款额度计算公式
    - 案例分析
  - 03 计算工具
  - 04 Python实现

01 等额本息

每月还款数额计算公式

M = P × R × ( 1 + R ) N ( 1 + R ) N − 1 M = P \times \frac{R \times (1+R)^{N}} {(1+R)^N - 1} M=P×(1+R)N−1R×(1+R)N

字母	描述
M	每月还款数额
P	贷款金额
R	月利率 R = 年利率 12 \quad R = \frac{年利率}{12} R=12年利率
N	还款期数

案例分析：

(1) 你购买了一所价格100万元的房子，首付为30%，使用的是旧版基准利率4.9%，贷款期限为30年，计算每月还款(M)、利息总额(M×N-P)、本息合计(M×N)

解：
首付金额 = 100 万 × 30 % = 30 万 =100万 \times 30\% = 30万 =100万×30%=30万
贷款金额 = 100 万 − 30 万 = 70 万 = 100万 - 30万 = 70万 =100万−30万=70万
每月还款(M)：
R = 4.9 % 12 N = 12 × 30 P = 70 万 M = P × R × ( 1 + R ) N ( 1 + R ) N − 1 = 3715 ( 元 ) \begin{aligned} R & = \frac{4.9\%}{12} \quad \quad \quad N = 12\times 30 \quad \quad P = 70万 \\ M & = P \times \frac{R \times(1+R)^N}{(1+R)^N-1} = 3715(元) \end{aligned} RM=124.9%N=12×30P=70万=P×(1+R)N−1R×(1+R)N=3715(元)
本息合计： M × N = 133.74 (万元)
利息总额： M × N - P = 63.74 (万元)

02 等额本金

每月还款额度计算公式

M i = P N + ( P − X i ) × R M_i = \frac{P}{N} + (P- X_i) ×R Mi=NP+(P−Xi)×R

字母	描述
M i M_i Mi	每月还款数额
P P P	贷款金额
R R R	月利率 R = 年利率 12 \quad R = \frac{年利率}{12} R=12年利率
N N N	还款期数
X i X_i Xi	已归还本金 X i = i N × P \quad X_i = \frac{i}{N}×P Xi=Ni×P

案例分析

(1) 你购买了一所价格100万元的房子，首付为30%，使用的是旧版基准利率4.9%，贷款期限为30年，计算每月还款、利息总额、本息合计
解：
首付金额 = 100 万 × 30 % = 30 万 =100万 \times 30\% = 30万 =100万×30%=30万
贷款金额 = 100 万 − 30 万 = 70 万 = 100万 - 30万 = 70万 =100万−30万=70万
首月还款( M 1 M_1 M1)：
R = 4.9 % 12 N = 12 × 30 P = 70 万 X 1 = 1 N × P = 1944.4 元 M 1 = P N + ( P − X 1 ) × R = 4802.78 元 \begin{aligned} R & = \frac{4.9\%}{12} \quad \quad \quad N = 12\times 30 \quad \quad P = 70万\\ X_1 & = \frac{1}{N} \times P = 1944.4元 \\ M_1 & = \frac{P}{N} + (P- X_1) ×R = 4802.78 元 \end{aligned} RX1M1=124.9%N=12×30P=70万=N1×P=1944.4元=NP+(P−X1)×R=4802.78元
本息合计：还款总额 =（还款月数+1）×贷款额×月利率/2+ 贷款额
S = ∑ i N M i = ( N + 1 ) × P × R 2 + P = 121.59 万元 S = \sum_i^NM_i = (N+1) \times P \times \frac{R}{2} + P = 121.59 万元 S=i∑NMi=(N+1)×P×2R+P=121.59万元
利息总额： S − P = 121.59 万元 − 70 万元 = 51.59 万元 S-P = 121.59 万元 - 70万元 = 51.59 万元 S−P=121.59万元−70万元=51.59万元

03 计算工具

参考1: 房贷计算器//www.baiozhuntuixing.com/daikuan.aspx
参考2: 安居客房贷计算器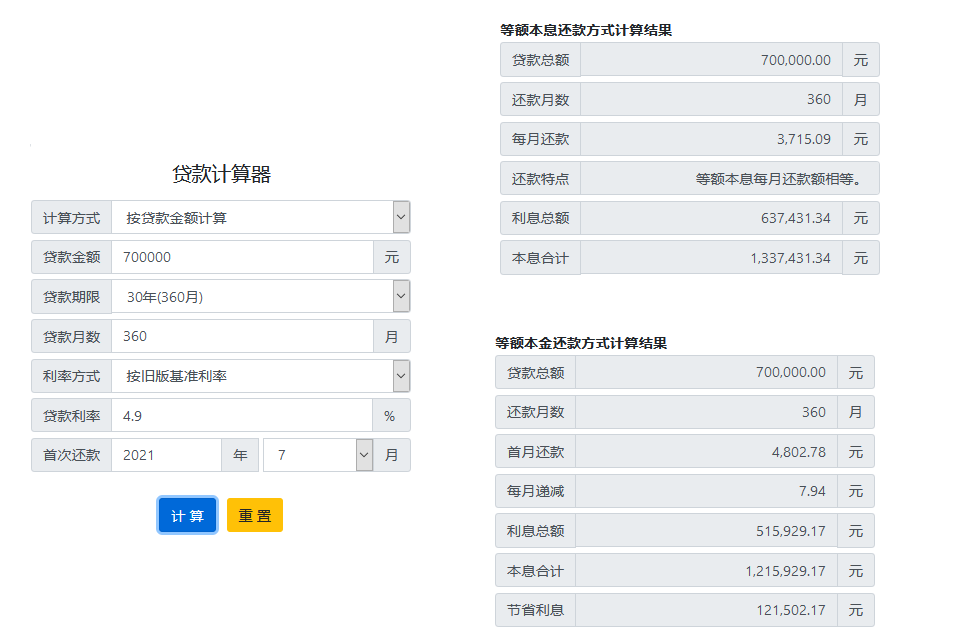
在这里插入图片描述

04 Python实现

"""
你购买了一所价格100万元的房子，首付为30%，
使用的是旧版基准利率4.9%，贷款期限为30年，
分别用等额本息和等额本金计算，每月还款、利息总额、本息合计
"""
import numpy as np
# 01 等额本息计算器
P = 70 * 10**4        # 70万
R = 4.9/100 / 12.0    # 4.9%的年利率
N = 12 * 30        # 30年
M = P * (R*(1+R)**N) / ((1+R)**N-1)
print("===============等额本息==============")
print("每月还款: %0.2f 元" % M)
print("本息合计: %0.2f 万元" % (M*N * 10**(-4)))
print("利息总和: %0.2f 万元" % ((M*N-P) * 10**(-4)))
print()
# 02 等额本金计算
# 每月还本付息金额=（本金/还款月数）+（本金-累计已还本金）×月利率
X = 0.0
ret = 0.0    
M = np.zeros(N)
for i in range(1,N+1):
    M[i-1] = (P/N) + (P-X) * R    # 每月还款金额
    X = i/N * P                    # 已归还本金
    ret = ret + M[i-1]            # 已归还金额 不等于 已归还本金
print("===============等额本金==============")
# 首月还款金额
print("首月还款: %0.2f 元" % M[0])
# 每月递减金额
print("每月递减: %0.2f 元" % (M[0]-M[1]))
# 还款总额
# print(ret * 10**(-4))
# 还款总额 =（还款月数+1）×贷款额×月利率/2+ 贷款额
end_sum = (N+1) * P * R /2 + P
print("本息合计: %0.2f 万元" % (end_sum * 10**(-4)))
print("利息总和: %0.2f 万元" % ((end_sum-P) * 10**(-4)))