机器学习 | 【05】聚类算法

一时失言乱红尘 2022-09-04 11:50 473阅读 0赞

文章目录

      • 聚类算法
        • 1、简介
          • 1.1 应用
        • 2、API简介
        • 3、实现流程
          • 3.1 聚类步骤
        • 4、模型评估
          • 4.1 误差平方和
          • 4.2 肘方法【K值确定】
          • 4.3 轮廓系数法
          • 4.4 CH系数
        • 5、小结
        • 6、优化算法
          • 6.1 Canopy算法
          • 6.2 K-means++
          • 6.3 K-means++
          • 6.4 k-medoids（中心聚类算法）
        • 7、特征降维
          • 7.1 降维
          • 7.2 特征选择
          • 7.3 相关系数
          • 7.4 主成分分析（PCA）

聚类算法

1、简介

  • 使用不同的聚类准则，产生的聚类结果不同。
  • 一种典型的无监督学习的算法，主要用于将相似的样本自动归到一个类别上；
  • 常用欧式距离算法。
1.1 应用
  • 用户画像，广告推荐，Data Segmentation，搜索引擎的流量推荐，恶意流量识别；
  • 基于位置信息的商业推送，新闻聚类，筛选排序；
  • 图像分割，降维，识别；离群点检测；信用卡异常消费；发掘相同功能的基因片段。

2、API简介

sklearn.cluster.KMeans(n_ clusters=8)

  • n_clusters：开始的聚类中心数量

    • 整型，缺省值=8，生成的聚类数，即产生的质心(centroids) 数。
  • estimator.fit(x)；
  • estimator.predict(x)；

  • estimator.fit_predict(x)；

    • 计算聚类中心并预测每个样本类别，相当于先调用fit(x),然后再调用predict(x)；
  1. # _*_ coding:utf-8 _*_
  2. # @File : KMeanDemo.py
  3. # @Author: Jxiepc
  4. # @Time : 2021-08-13 16:18
  5. import matplotlib.pyplot as plt
  6. from sklearn import datasets
  7. from sklearn.cluster import KMeans
  8. from sklearn.metrics import calinski_harabasz_score
  10. X,y = datasets.make_blobs(n_samples=1000, n_features=2,
  11.                           centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
  12.                           cluster_std=[0.4, 0.1, 0.1, 0.1], random_state=22)
  13. """ Parameters ---------- n_samples : 平均分配的点数总数 n_features : 每个样本的特征数量 centers : 生成的中心数量，或固定的中心位置 cluster_std : 簇的标准差 Returns ------- X : ndarray of shape (n_samples, n_features)特征值 y : ndarray of shape (n_samples,)目标值 """
  14. estimator = KMeans(n_clusters=2, random_state=22)
  15. """ Parameters ---------- n_clusters : 类别的数量 """
  16. y_pre = estimator.fit_predict(X)
  18. plt.scatter(X[:, 0], X[:, 1], c=y_pre)
  19. plt.show()
  20. result = calinski_harabasz_score(X, y_pre)
  21. print(result)

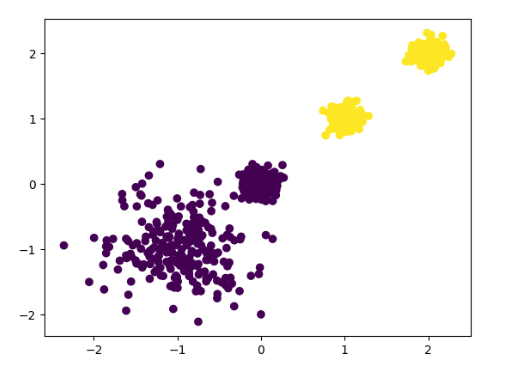
在这里插入图片描述

3、实现流程

K-means：

  • K：初始中心点个数（聚类数）；
  • means：求中心到其他数据点聚类的平均值。
3.1 聚类步骤
  • 随机设置K个特征空间内的点作为初始的聚类中心；
  • 对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别；
  • 接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）；
  • 如果计算得出的新中心点与原中心点一样(质心不再移动)，那么结束，否则重新进行第二步过程。

4、模型评估

4.1 误差平方和

在k-means中的应用：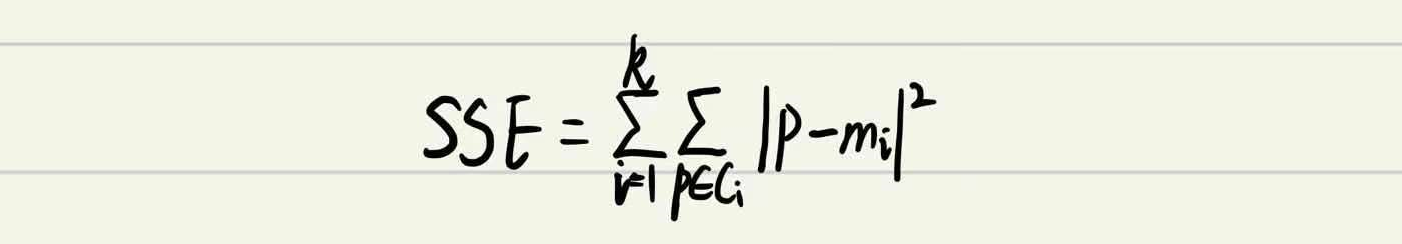
在这里插入图片描述

4.2 肘方法【K值确定】

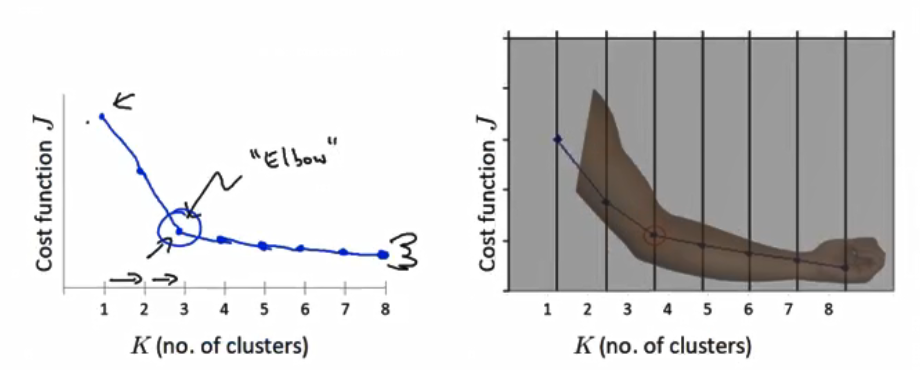
在这里插入图片描述

下降点突然变缓为最佳的k值。

4.3 轮廓系数法

结合了聚类的凝聚度和分离度，用于评估聚类的效果；S值越大越好

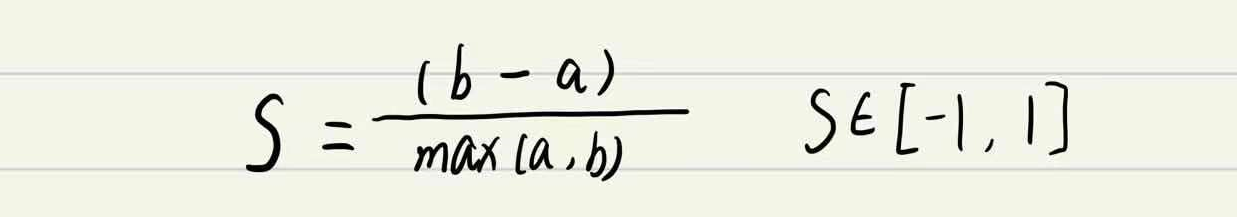
在这里插入图片描述

  • a：为样本点到其他点的平均值；
  • b：为样本点到其他簇的最小值；
  • 目的：内部距离最小化，外部距离最大化。

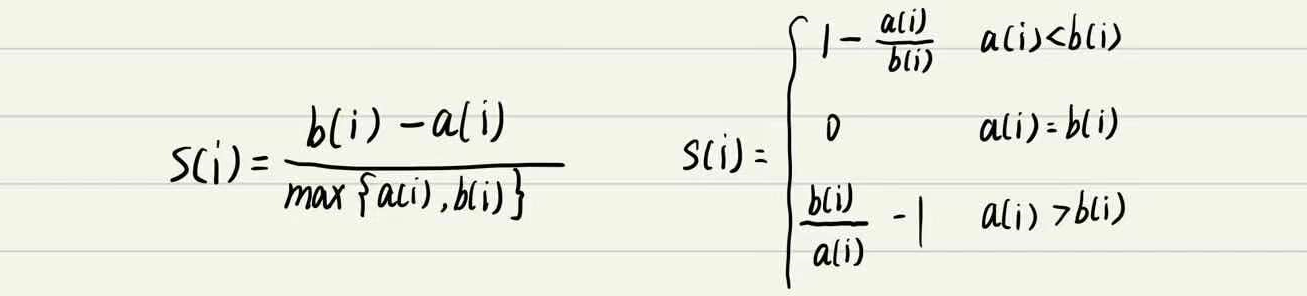
在这里插入图片描述

4.4 CH系数

类别内部数据的距离平方和越小越好，类别之间的距离平方和越大越好；

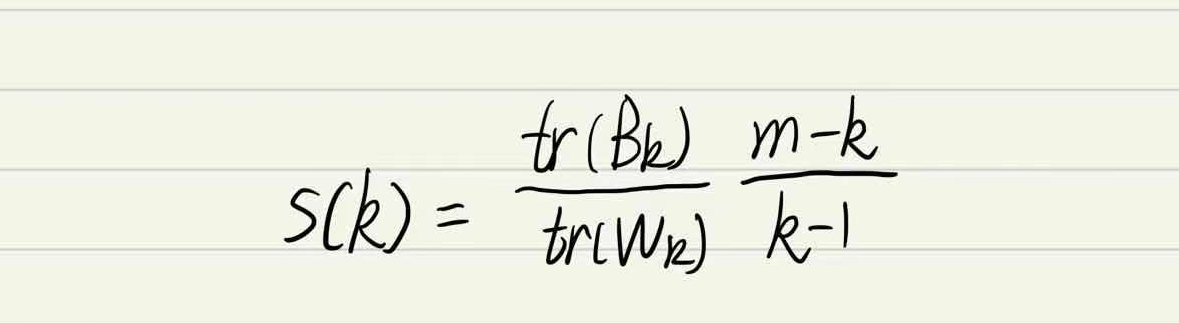
在这里插入图片描述

  • tr：矩阵的迹；
  • Bk：类别之间的协方差矩阵；
  • Wk：类别内部数据的协方差矩阵。

CH目的：用尽量少的类别聚类尽量多的样本，同时获得较好的聚类效果。

5、小结

  • K-means优点：

    • 原理简单（靠近中心点），实现容易；
    • 聚类效果中上（依赖K的选择）；
    • 空间复杂度O(N)，时间复杂度O(KN)；
    • N为样本点个数，K为中心点个数，I为迭代次数。

  • K-means缺点：

    • 对离群点，噪声敏感（中心点易偏移）；
    • 很难发现大小差别很大的簇及进行增量计算；
    • 结果不一定是全局最优，只能保证局部最优（与K的个数及初值选取有关）；

6、优化算法

6.1 Canopy算法

让初始点的选择更加合理。

优点：

  • Kmeans对噪声抗干扰较弱，通过Canopy对比，将较小的NumPoint的Cluster直接去掉有利于抗干扰；
  • Canopy选择出来的每个Canopy的centerPoint作为K会更精确；
  • 只是针对每个Canopy的内做Kmeans聚类，减少相似计算的数量。
    缺点：
  • 法中T1、T2的确定问题，依旧可能落入局部最优解。
6.2 K-means++

让选择的质心尽可能分散；

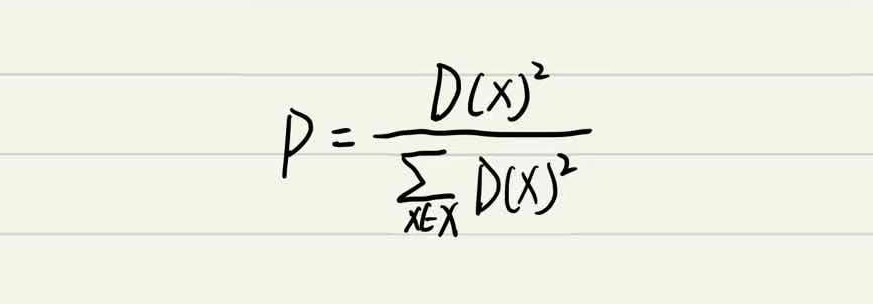
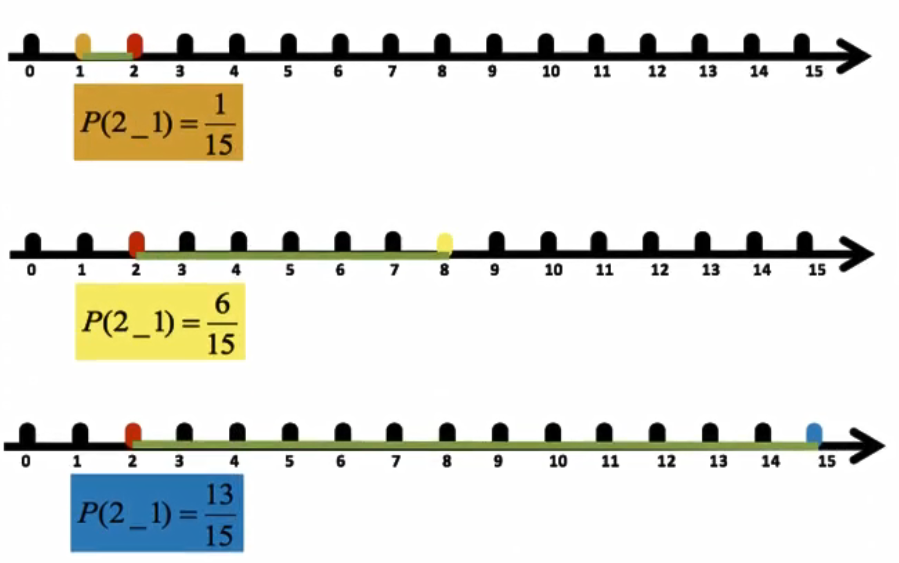
在这里插入图片描述

在这里插入图片描述

6.3 K-means++

步骤：

  • 所有点作为一个簇；
  • 将该簇一分为二；
  • 选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇；
  • 以此进行下去，直到簇的数目等于用户给定的数目k为止。
6.4 k-medoids（中心聚类算法）

与k-means的区别在与中心点的选取；

  • 从当前簇中选取到其他所有点的距离之和最小的点作为中心点。

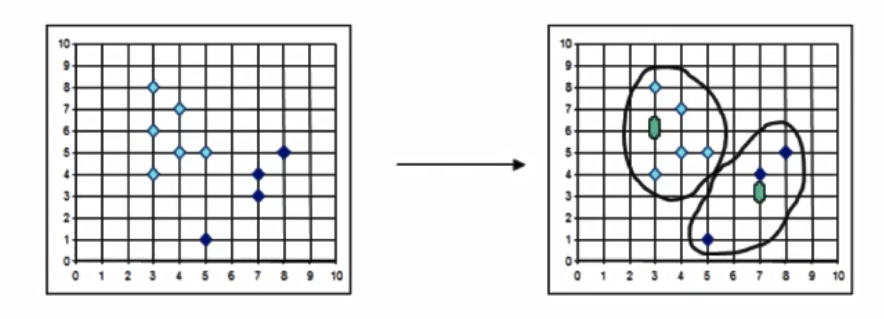
在这里插入图片描述
算法流程：

  • 总体n个样本点中任意选取k个点作为medoids；
  • 按照与medoids最近的原则，将剩余的n-k个点分配到当前最佳的medoids代表的类中；
  • 对于第i个类中除对应medoids点外的所有其他点，按顺序计算当其为新的medoids时，代价函数的值，遍历所有可能，选取代价函数最小时对应的点作为新的medoids；
  • 重复2-3的过程，直到所有的medoids点不再发生变化或已达到设定的最大迭代次数；
  • 产出最终确定的k个类。

小结

k- medoids只能对小样本起作用，样本大，速度慢，当样本多的时候，所以k-means的应用明显比k-medoids多。

7、特征降维

7.1 降维

降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组“不相关”主变量的过程；

降低随机变量的个数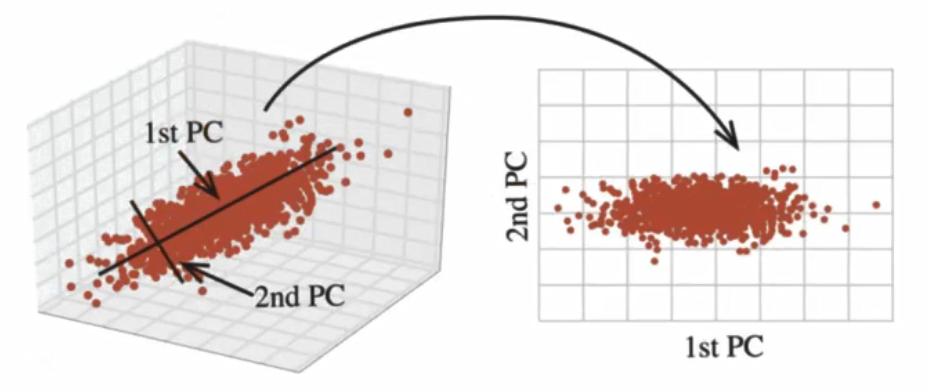
在这里插入图片描述

相关特征

降维的俩种方式：

  • 特征选择；
  • 主成分分析
7.2 特征选择

定义

数据中包含冗余或无关变量(或称特征、属性、指标等)，旨在从原有特征中找出主要特征。

方法：

  • Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联

    • 方差选择法：低方差特征过滤；
    • 相关系数；

  • Embedded (嵌入式):算法自动选择特征(特征与目标值之间的关联)

    • 决策树：信息熵、信息增益；
    • 正则化：L1、 L2；
    • 深度学习：卷积等；

低方差特征过滤

删除低方差的一些特征，前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。

  • 特征方差小：某个特征大多样本的值比较相近；
  • 特征方差大：某个特征很多样本的值都有差别。

API

  • sklearn.feature_selection.VarianceThreshold(threshold=0.0)

    • 删除所有低方差特征；

    • Variance.fit_transform(X)；

      • X：numpy array格式的数据[n_samples, n_features]；
      • 返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。
7.3 相关系数
  • 皮尔逊
  • 斯皮尔曼

皮尔逊相关系数

  • 作用：
    反映变量之间相关关系密切程度的统计指标。

  • 特点：
    相关系数的值介于-1与1之间，其性质如下:

    • 当r>0时，表示两变量正相关，r<0时， 两变量为负相关；
    • 当r=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系；
    • 当0<|r|<1时， 表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱；
    • 一般可按三级划分：|r|<0.4为低度相关；0.4s|r|<0.7为显著性相关；0.7s|r|<1为高度线性相关。
  • API
    scipy.stats.pearsonr

斯皮尔曼相关系数(Rank IC)

  • 作用：
    反映变量之间相关关系密切程度的统计指标

  • 特点：

    • 斯皮尔曼相关系数表明X (自变量)和Y (因变量)的相关方向。如果当X增加时，Y趋向于增加，斯皮尔曼相关系数则为正。
    • 与之前的皮尔逊相关系数大小性质一样，取值[-1, 1]之间。
  • API：
    scripy.stats.spearmanr
7.4 主成分分析（PCA）
  • 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量；
  • 作用：是数据维数压缩，尽可能降低原数据的维数(复杂度)，损失少量信息；
  • 应用：回归分析或者聚类分析当中。

API
sklearn.decomposition.PCA(n components=None)

  • 将数据分解为较低维数空间；

  • n_components：

    • 小数：表示保留百分之多少的信息；
    • 整数：减少到多少特征；
  • PCA.fit_transform(X) X:numpy array格式的数据[n_samples, n_features]；
  • 返回值：转换后指定维度的array。

发表评论

表情：
评论列表 （有 0 条评论，473人围观）

还没有评论，来说两句吧...

相关阅读

    相关 python机器学习10:聚类算法

    1.K均值聚类 1.K均值聚类的工作原理： 假设我们的数据集中的样本因为特征不同，像下沙堆一样散步在地上，K均值算法会在小沙堆上插上旗子。而第一遍插的旗子并不能完美

    灰太狼灰太狼/ 0 赞/ 440 阅读