Pytorch与深度学习 —— 5. 什么是循环神经网络（Recurrent Neural Network）

你的名字 2022-09-09 04:37 206阅读 0赞

> 在前面的章节里，给大家介绍了什么是神经网络，从基础概念出发，为了识别MNIST数据集，我们搭建了一个[全连接网络][Link 1]，然后又把卷积的概念引入进来后，给大家介绍了全连接网络的一种改进型——[卷积神经网络][Link 2]。而且发现，在没有优化网络结构的前提下，仅使用通用模型就取得了98%的准确率，优于全连接网络的95%准确率。  
> 现在，把目光从擅长空间数据处理的卷积神经网络（CNN）转入到擅长时序任务处理的循环神经网络（RNN），又来看看它是怎么工作。

### 文章目录 ###

*  为什么使用循环神经网络
 *   *  ECG信号
     *  语音识别
 *  RNN的基本结构
 *   *  斐波那契数列
     *  RNN网络的计算规则

# 为什么使用循环神经网络 #

尽管FNN或者DNN（全连接网络，在一些论文里又被称为密集神经网络 Dense Neural Network），是所有神经网络的基础，理论上FNN也是可以用来处理时序任务，但事实上有比FNN更擅长时序任务的网络模型，这一类模型通常称为循环神经网络——RNN。

我们生活种常见的数据类型，如果简单的分析会发现它们具有时间或空间方面的特性。比方说空间特性的图片，和时间特性的音频。当然也有同时具备这两种特性的，比如说视频。

## ECG信号 ##

与CNN专注于空间特征分析不同，RNN更擅长时间序列特征的分析。举例来说，心电数据ECG（Electrocardiograph），单个心电数据从其波形数据上有T波、R波等，对于心内科的医生来说，通过看心电图，可以判断出心脏工作状态是否正常，是否有心颤等危险信号。

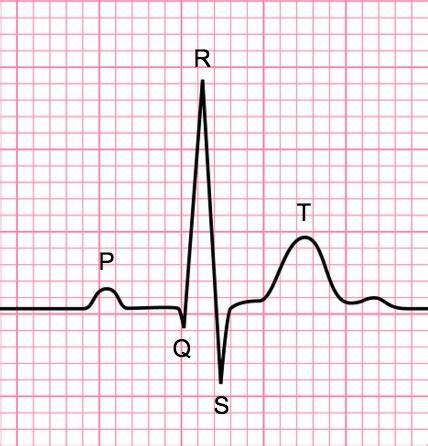
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_12_color_FFFFFF_t_70_g_se_x_16_pic_center]

而通过一个观察周期的心电图信息，例如下面这张图，心内科医生又可以很快判断出窦性心律过快、过慢或者心律不齐等问题，从而为制定合理诊断提供依据。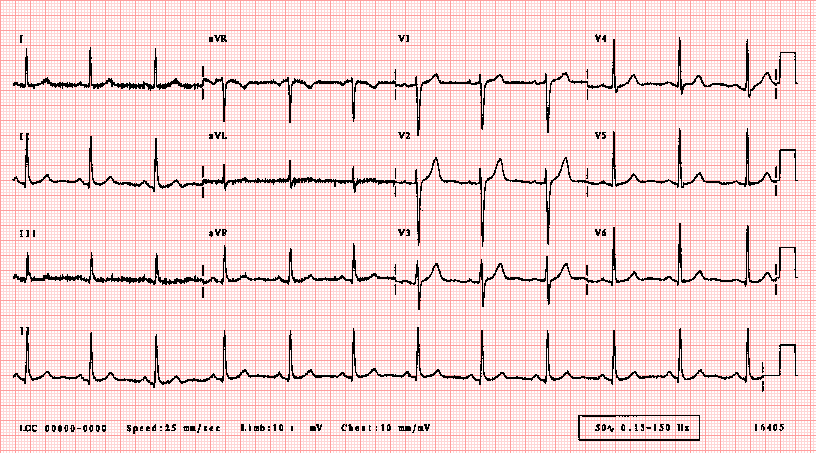  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center]  
可以看出，这一类数据有很强的顺序关联关系，如果想要分析和处理这一类数据，就要求我们一定以一定的顺序方向去读取和分析数据。

## 语音识别 ##

![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_17_color_FFFFFF_t_70_g_se_x_16_pic_center]

如果我们想通过语音与计算机进行交互，直接通过语音是无法直接应用的。至少我们要先把语音转化为文本数据后，才能分析出用户的意图。对于计算机来说，没有处理过的语音信息，就是一串带有噪音的模拟信号而已。

虽然说CNN网络在最新的一些论文里也被用在了时序数据上，但是在时序数据的处理上，有比CNN更擅长的网络技术，这一类网络被称为循环神经网络（RNN：Recurrent Neural Network）。

# RNN的基本结构 #

## 斐波那契数列 ##

为了让你能理解RNN是怎么工作的，先让我们回顾一下著名的斐波那契数列吧，它的数列表达形式是这样的：

F n = F ( n − 1 ) + F ( n − 2 ) F\_n = F\_\{(n - 1)\} + F\_\{(n - 2)\} Fn=F(n−1)\+F(n−2)

计算方法是从两个1开始，即数列  F \\mathbb\{F\} F 的  F 0 F\_0 F0,  F 1 F\_1 F1 为1，这样  F 2 = 2 , F 3 = 3 ， ⋯ F\_2 = 2, F\_3 = 3， \\cdots F2=2,F3=3，⋯

\[ 1 , 1 , 2 , 3 , 5 , 8 , 13 , ⋯   \] \[1, 1, 2, 3, 5, 8, 13, \\cdots\] \[1,1,2,3,5,8,13,⋯\]

我们用计算图的形式表示这个计算过程：

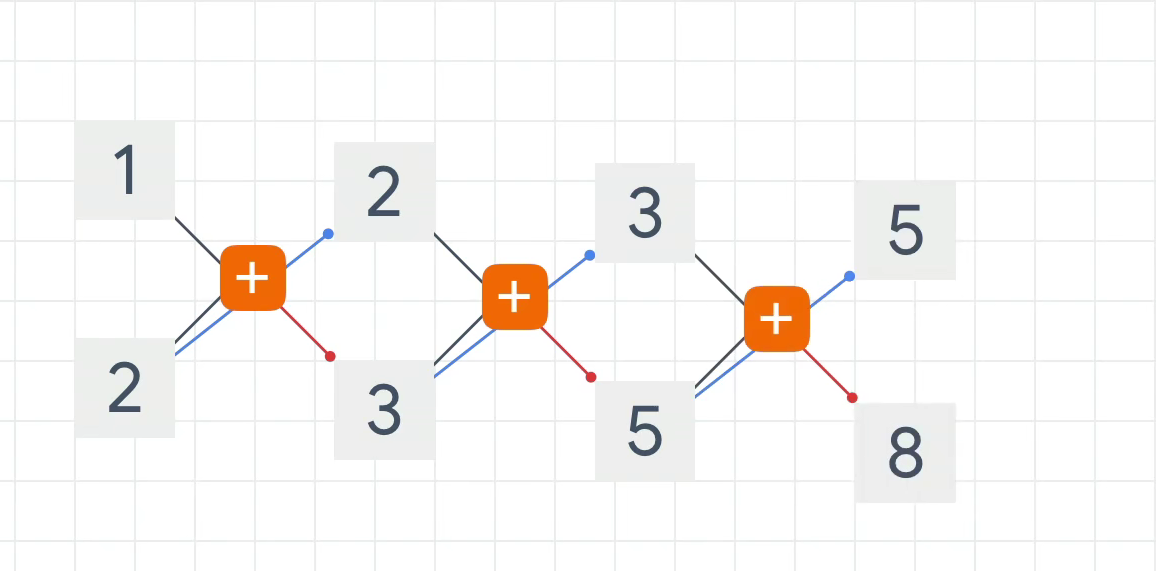
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center 1]  
可以看到，1 与 2 相加得到3，2 参加下一轮计算，与 3 相加得到5，以此类推。

如果我们以这个图下方的数当作输入  X X X，上方的数字为输出  O O O，那么我们要得到  O n O\_n On 的输出可以看到它依赖于上一时刻的  O ( n − 1 ) O\_\{(n-1)\} O(n−1) 以及当前  X n X\_n Xn 的输入。

用这个例子是为了说明，RNN的工作原理和斐波那契数列的运算规则很相似

## RNN网络的计算规则 ##

我们来看一下一个标准的RNN网络的计算公式

h t = tanh ⁡ ( W i h x t + b i h + W h h h ( t − 1 ) + b h h ) h\_t = \\tanh (W\_\{ih\} x\_\{t\} + b\_\{ih\} +W\_\{hh\} h\_\{(t−1)\} + b\_\{hh\}) ht=tanh(Wihxt\+bih\+Whhh(t−1)\+bhh)

要知道  y = W x + b \\mathbf\{y\} = \\mathbf\{W\} \\mathbf\{x\} + \\mathbf\{b\} y=Wx\+b 是一个标准线性公式，如果我们令

\{ y i = W i h x t + b i h y h = W h h h t − 1 + b h h \\left\\\{\\begin\{matrix\} \\mathbf\{y\_i\} = W\_\{ih\} x\_\{t\} + b\_\{ih\} \\\\ \\mathbf\{y\_h\} = W\_\{hh\} h\_\{t-1\} + b\_\{hh\} \\end\{matrix\}\\right. \{ yi=Wihxt\+bihyh=Whhht−1\+bhh

上面这个公式就表示为：

h t = tanh ⁡ ( y i + y h ) h\_t = \\tanh (\\mathbf\{y\_i\} + \\mathbf\{y\_h\}) ht=tanh(yi\+yh)

其中  y i \\mathbf\{y\_i\} yi 表示的就是与输入相关的线性公式， y h \\mathbf\{y\_h\} yh 就是在RNN中经常被提到的隐藏层，你可以理解为对上一次计算结果的保存。如果用图表示RNN计算过程，那么就是下面这个样子的：

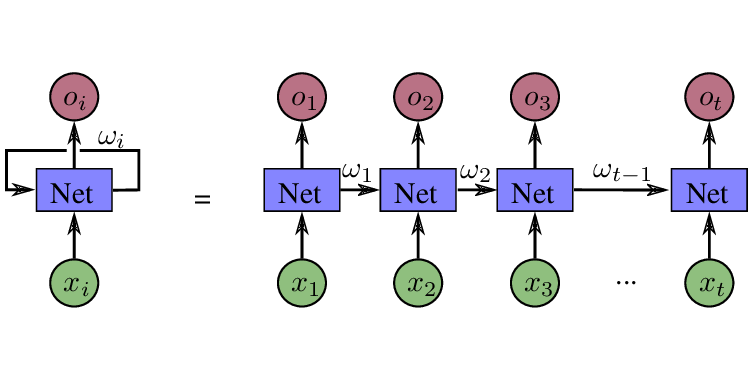
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center 2]

一个基本的RNN节点会经常被描写成这样的结构：

*  当前输入数据的  X i X\_i Xi，
 *  用于回馈并计入下一次计算的  ω i \\omega\_i ωi 也就是隐藏层  y h \\mathbf\{y\_h\} yh 的权重
 *  以及每一次计算输出的  O i O\_i Oi。

由于  y h \\mathbf\{y\_h\} yh 矩阵通常保存了上一次的计算结果，所以它的矩阵维度事实上是可以和 参与计算  O i O\_i Oi 的权重矩阵维度一致，尽管事实上在Pytorch提供的相关模型里也是这么设置的。**但是要指出的是， O i O\_i Oi 与  ω i \\omega\_i ωi 虽然有关系，但不是一回事，有些教科书或者讲师可能会说它们是一回事，但其实它们的关系更像是双胞胎兄弟，而不是同一个人。**

用线性层的代码直接实现一个RNN网络的话，通常是这样的：

class RNN(torch.nn.Module):
    
        """ $h_t = tanh(W_{ih}x_t + b_{ih} + W_{hh}h_{(t-1)} + b_{hh})$ input_size: encoded data size, could be in one-hot-vector, or ascii based, and etc. hidden_size: hidden state, to recorde previous computed weights output_size: output features to predicate """
    
        def __init__(self, input_size, hidden_size, output_size):
            super(RNN, self).__init__()
    
            self.hidden_size = hidden_size
    
            self.i2h = torch.nn.Linear(input_size + hidden_size, hidden_size)
            self.i2o = torch.nn.Linear(input_size + hidden_size, output_size)
            self.softmax = torch.nn.LogSoftmax(dim=1)
    
        def forward(self, x, h0):
            """ x: encoded substance of a sequence, for instance, 'a' to 'apple' ho: previous computed features of hidden layer, if no knowledges need to passed in first recurrent time, given a tensor with all-zero to the net """
            combined = torch.cat((x, h0), 1)
            h0 = self.i2h(combined)
            output = self.i2o(combined)
            output = self.softmax(output)
            return output, h0

*  基本结构由两个线性计算单元及一个Softmax构成；
 *  运算的时候，要传入当前的数据，以及先前的隐藏层数据；
 *  数据通过cat命令转化为一个完整的张量 **combined**；
 *  **combined** 分别送给负责隐藏层的 i2h 单元，和负责输出的 i2o 单元；
 *  i2o单元得到的结果再通过 softmax 后返回给用户。

之所以说它们是一样的唯一原因，仅仅是如果隐藏层输出特征维度与 i2o 输出的特征维度一致的时候， h 0 h\_0 h0 和 没有 softmax 处理过的 output 才是一样的。

通过上面的说明，我们可以知道 RNN的计算节点，本质上就是线性层堆叠，所以它并没有你想象中的那么难理解。

[Link 1]: https://seagochen.blog.csdn.net/article/details/119754293
[Link 2]: https://seagochen.blog.csdn.net/article/details/119940591
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_12_color_FFFFFF_t_70_g_se_x_16_pic_center]: /images/20220829/9dd425ecfae948d290dabd1bfed277cf.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center]: /images/20220829/0596d7b002c04edea0d1020bf270caf9.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_17_color_FFFFFF_t_70_g_se_x_16_pic_center]: /images/20220829/5ad54da6d4a84c15849a7b2a2ca3f893.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center 1]: /images/20220829/5b62b605d3e7425c956c3a14cb4e627b.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5omT56CB55qE6Zi_6YCa_size_20_color_FFFFFF_t_70_g_se_x_16_pic_center 2]: /images/20220829/05dbe1b172554c09a4d510a74b090d4c.png