leetcode 473. Matchsticks to Square | 473. 火柴拼正方形（递归）-蒲公英云

leetcode 473. Matchsticks to Square | 473. 火柴拼正方形（递归）

题目

https://leetcode.com/problems/matchsticks-to-square/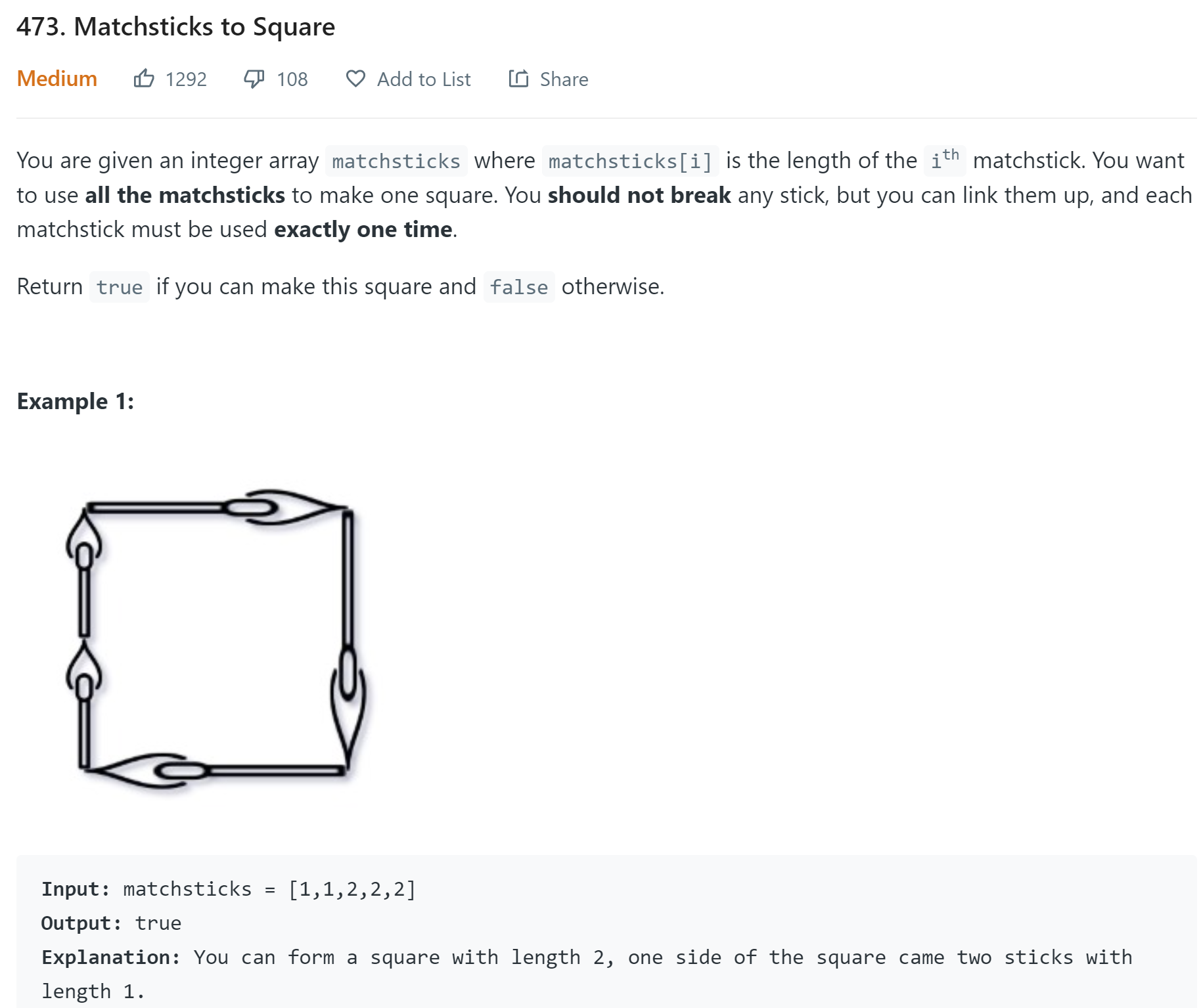
在这里插入图片描述

题解

看了 hint 之后，才有思路。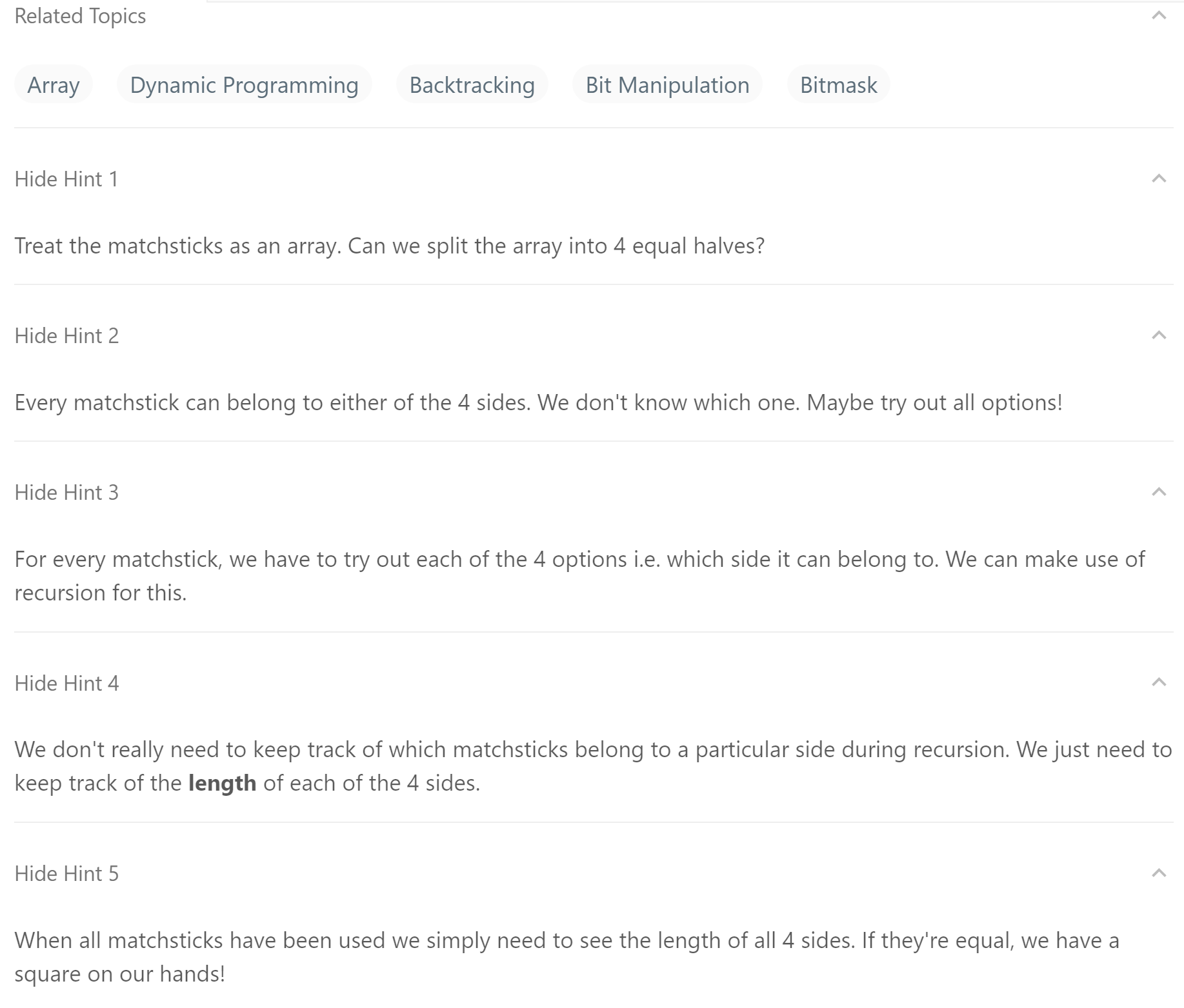
在这里插入图片描述

讨论区有个人说得好：

This solution should mention that this problem is an instance of the well-known Bin Packing Problem, which has been proven to be NP-complete, so it is not possible to implement a solution that takes less than exponential time. This would be a very important fact for the candidate to identify, because they otherwise will likely spin their wheels trying to identify a polynomial-time solution.

Once you’ve identified that the problem is NP-complete, you know that you’ll just have to implement a “brute force” solution, and the only task remaining is to look for opportunities to reduce the amount of work you need to do via pruning, memoization, etc.

…

Exactly. In fact second solution is over-engineering because there isn’t an actual improvement in big o time complexity.

If I was the interviewer, if the candidate identified that it’s a variant of bin-packing, therefore NP-complete, and gave a clean backtracking solution, that would be full marks.

class Solution { 
    public boolean makesquare(int[] arr) { 
        Arrays.sort(arr);
        int sum = 0;
        for (int m : arr) { 
            sum += m;
        }
        if (sum % 4 != 0) return false;
        return process(arr, arr.length - 1, 0, 0, 0, 0, sum / 4);
    }
    public boolean process(int[] arr, int i, int l1, int l2, int l3, int l4, int target) { 
        if (i < 0) return l1 == target && l2 == target && l3 == target && l4 == target;
        if (l1 > target || l2 > target || l3 > target || l4 > target) return false;
        return process(arr, i - 1, l1 + arr[i], l2, l3, l4, target) ||
                process(arr, i - 1, l1, l2 + arr[i], l3, l4, target) ||
                process(arr, i - 1, l1, l2, l3 + arr[i], l4, target) ||
                process(arr, i - 1, l1, l2, l3, l4 + arr[i], target);
    }
}