L1与L2正则化
0 公式
定义 L L L为loss
L1正则
m i n L + C ⋅ ∥ w ∥ 1 min L + C · \left \|w \right \|_1 minL+C⋅∥w∥1
L2正则
m i n L + C ⋅ ∥ w ∥ 2 2 min L + C · \left \|w \right \|_2^2 minL+C⋅∥w∥22
1 结构风险最小化角度
在经验风险最小化的基础上(也就是训练误差最小化),尽可能采用简单的模型,以此提高泛化预测精度。
假设X为一个二维样本,那么要求解参数 w w w也是二维,原函数曲线等高线:

加入L1和L2后的图像

1.1 认知
1、如果不加L1和L2正则化的时候,对于线性回归这种目标函数凸函数的话,我们最终的结果就是最里边的紫色的小圈圈等高线上的点。
2、当加入L1正则化的时候,我们先画出 ∣ w 1 ∣ + ∣ w 2 ∣ = F |w_1| + |w_2| = F ∣w1∣+∣w2∣=F的图像,也就是一个菱形,代表这些曲线上的点算出来的1范数 ∣ w 1 ∣ + ∣ w 2 ∣ |w_1| + |w_2| ∣w1∣+∣w2∣都为F。那我们现在的目标是不仅是原曲线算得值要小(越来越接近中心的紫色圈圈),还要使得这个菱形越小越好(F越小越好)
1.2 求解
1、以同一条原曲线目标等高线来说,现在以最外圈的红色等高线为例,我们看到,对于红色曲线上的每个点都可以做一个菱形,根据上图可知,当这个菱形与某条等高线相切(仅有一个交点)的时候,这个菱形最小,上图相割对比较大的两个菱形对应的1范数更大。用公式说这个时候能使得在相同的 1 N ⋅ ∑ i = 1 i = N ( y i − w T x i ) 2 \frac{1}{N}·\sum_{i=1}^{i=N}(y_i-w^Tx_i)^2 N1⋅∑i=1i=N(yi−wTxi)2下,由于相切的时候的 C ⋅ ∥ w ∥ 1 C · \left \|w \right \|_1 C⋅∥w∥1小,也就是 ∣ w 1 ∣ + ∣ w 2 ∣ |w_1| + |w_2| ∣w1∣+∣w2∣小,所以可以使得 1 N ⋅ ∑ i = 1 i = N ( y i − w T x i ) 2 + C ⋅ ∥ w ∥ 1 \frac{1}{N}·\sum_{i=1}^{i=N}(y_i-w^Tx_i)^2 + C · \left \|w \right \|_1 N1⋅∑i=1i=N(yi−wTxi)2+C⋅∥w∥1更小。
2、有了1.的说明,我们可以看出,最终加入L1范数得到的解,一定是某个菱形和某条原函数等高线的切点。现在有个比较重要的结论来了,我们经过观察可以看到,几乎对于很多原函数等高曲线,和某个菱形相交的时候及其容易相交在坐标轴(比如上图),也就是说最终的结果,解的某些维度及其容易是0,比如上图最终解是 ,这也就是我们所说的L1更容易得到稀疏解(解向量中0比较多)的原因。
3、求导来证明,具体的证明这里有一个很好的答案了,简而言之就是假设现在我们是一维的情况下 h ( w ) = f ( w ) + C ⋅ ∥ w ∥ 1 h(w) = f(w) + C · \left \|w \right \|_1 h(w)=f(w)+C⋅∥w∥1。那么要使得0点成为最值可能的点,虽然在0点不可导,但是我们只需要让0点左右的导数异号, h l e f t ′ ( w ) ⋅ h r i g h t ′ ( w ) = ( f ′ ( 0 ) + C ) ⋅ ( f ′ ( 0 ) − C ) < 0 h_{left}^{‘}(w) · h_{right}^{‘}(w) = (f^{‘}(0)+C)·(f^{‘}(0)-C) < 0 hleft′(w)⋅hright′(w)=(f′(0)+C)⋅(f′(0)−C)<0,从而,当 C > ∣ f ′ ( 0 ) ∣ C > |f^{‘}(0)| C>∣f′(0)∣的情况下,0点是最值点。
4、当加入L2正则化的时候,分析和L1正则化是类似的,也就是说我们仅仅是从菱形变成了圆形而已,同样还是求原曲线和圆形的切点作为最终解。当然与L1范数比,我们这样求的L2范数的从图上来看,不容易交在坐标轴上,但是仍然比较靠近坐标轴。因此这也就是我们老说的,L2范数能让解比较小(靠近0),但是比较平滑(不等于0)。
综上所述,我们可以看见,加入正则化项,在最小化经验误差的情况下,可以让我们选择解更简单(趋向于0)的解。
2 贝叶斯先验概率的角度
现在再从贝叶斯学派的观点来看看正则化,即是我们先假设要求的参数服从某种先验分布,以线性回归为例子,我们之前讲过,用高斯分布的极大似然估计求线性回归。
1、在我们求解的时候,我们假设 Y ∣ X Y|X Y∣X服从 N ( W T X , σ ) N(W^TX, \sigma) N(WTX,σ)的正态分布,即概率密度函数 P ( Y ∣ X ; w ) = N ( W T X , σ ) P(Y|X; w) = N(W^TX, \sigma) P(Y∣X;w)=N(WTX,σ),然后利用极大似然估计求解参数 w w w.
m a x ( l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ) max (log \prod_{i=1}^{i=N}p(y_i|x_i; w)) max(logi=1∏i=Np(yi∣xi;w))
m i n ( − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ) min (-log \prod_{i=1}^{i=N}p(y_i|x_i; w)) min(−logi=1∏i=Np(yi∣xi;w))
2、在贝叶斯学派的观点看来,如果我们先假设参数 w w w服从一种先验分布 P ( w ) P(w) P(w),那么根据贝叶斯公式 P ( w ∣ ( X , Y ) ) ∼ P ( Y ∣ X , w ) ⋅ P ( w ) P(w|(X,Y)) \sim P(Y|X,w)·P(w) P(w∣(X,Y))∼P(Y∣X,w)⋅P(w),那我们利用极大似然估计求参数 w w w的时候,现在我们的极大似然函数就变成了:
m a x ( l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ⋅ p ( w ) ) = l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) + l o g ∏ i = 1 i = N p ( w ) max (log \prod_{i=1}^{i=N}p(y_i|x_i; w)·p(w)) = log \prod_{i=1}^{i=N}p(y_i|x_i; w) + log \prod_{i=1}^{i=N}p(w) max(logi=1∏i=Np(yi∣xi;w)⋅p(w))=logi=1∏i=Np(yi∣xi;w)+logi=1∏i=Np(w)
m i n ( − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ⋅ p ( w ) ) = − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) − l o g ∏ i = 1 i = N p ( w ) min (-log \prod_{i=1}^{i=N}p(y_i|x_i; w)·p(w)) = -log \prod_{i=1}^{i=N}p(y_i|x_i; w) - log \prod_{i=1}^{i=N}p(w) min(−logi=1∏i=Np(yi∣xi;w)⋅p(w))=−logi=1∏i=Np(yi∣xi;w)−logi=1∏i=Np(w)
对比发现,添加上正则化项以后,式子里多了一个求和项。
2.1 L1
假设我们让 w w w服从的分布为标准拉普拉斯分布,即概率密度函数为 0.5 e − ∣ x ∣ 0.5e^{-|x|} 0.5e−∣x∣,那么上公式多出的 − l o g ∏ i = 1 i = N p ( w ) - log \prod_{i=1}^{i=N}p(w) −log∏i=1i=Np(w)变成了 C ⋅ ∥ w ∥ 1 C · \left \|w \right \|_1 C⋅∥w∥1
m i n ( − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ⋅ p ( w ) ) = − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) + C ⋅ ∥ w ∥ 1 min (-log \prod_{i=1}^{i=N}p(y_i|x_i; w)·p(w)) = -log \prod_{i=1}^{i=N}p(y_i|x_i; w) + C · \left \|w \right \|_1 min(−logi=1∏i=Np(yi∣xi;w)⋅p(w))=−logi=1∏i=Np(yi∣xi;w)+C⋅∥w∥1
熟悉吧,这不就是加了L1范数的优化目标函数么。假设 w w w服从拉普拉斯分布的话,从下图可以看出 w w w的值取到0的概率特别大。也就是说我们提前先假设了 w w w的解更容易取到0。

2.2 L2
假设我们让 w w w服从的分布为标准正态分布,即概率密度函数为 1 2 π e − x 2 2 \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} 2π1e−2x2,那么上公式多出的 − l o g ∏ i = 1 i = N p ( w ) - log \prod_{i=1}^{i=N}p(w) −log∏i=1i=Np(w)变成了 C ⋅ ∥ w ∥ 2 2 C · \left \|w \right \|_2^2 C⋅∥w∥22
m i n ( − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) ⋅ p ( w ) ) = − l o g ∏ i = 1 i = N p ( y i ∣ x i ; w ) + C ⋅ ∥ w ∥ 2 2 min (-log \prod_{i=1}^{i=N}p(y_i|x_i; w)·p(w)) = -log \prod_{i=1}^{i=N}p(y_i|x_i; w) + C · \left \|w \right \|_2^2 min(−logi=1∏i=Np(yi∣xi;w)⋅p(w))=−logi=1∏i=Np(yi∣xi;w)+C⋅∥w∥22
熟悉吧,这不就是加了L2范数的优化目标函数么。假设 w w w服从标准正太分布的话,根据图我们可以看出,其实我们就是预先假设了 w w w的最终值可能取到0附近的概率特别大。

正则化之所以能够降低过拟合的原因在于,正则化是结构风险最小化的一种策略实现。给loss function加上正则化项,能使得新得到的优化目标函数h = f + normal,需要在f和normal中做一个权衡(trade-off),如果还像原来只优化f的情况下,那可能得到一组解比较复杂,使得正则项normal比较大,那么h就不是最优的,因此可以看出加正则项能让解更加简单,符合奥卡姆剃刀理论,同时也比较符合在偏差和方差(方差表示模型的复杂度)分析中,通过降低模型复杂度,得到更小的泛化误差,降低过拟合程度。
L1正则化和L2正则化:L1正则化就是在loss function后边所加正则项为L1范数,加上L1范数容易得到稀疏解(0比较多)。L2正则化就是loss function后边所加正则项为L2范数的平方,加上L2正则相比于L1正则来说,得到的解比较平滑(不是稀疏),但是同样能够保证解中接近于0(但不是等于0,所以相对平滑)的维度比较多,降低模型的复杂度。
欢迎关注微信公众号(算法工程师面试那些事儿),建号初期,期待和大家一起刷leecode,刷机器学习、深度学习面试题等,共勉~




























![[hbase] hbase的架构及其各角色功能 [hbase] hbase的架构及其各角色功能](https://image.dandelioncloud.cn/images/20230601/3b9ef42ad8a9409390d4df738d8087d6.png)
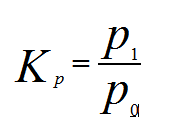



还没有评论,来说两句吧...