《A Graduate Course in Applied Cryptography》chapter 4 Block ciphers （1）-蒲公英云

原文教材与参考资料：

    Boneh Dan , Shoup Victor . A Graduate Course in Applied Cryptography\[J\].
    该书项目地址（可以免费获取）：http://toc.cryptobook.us/
   《现代密码学》（第四版）杨波.
    系列博客为对该教材的学习笔记（只包括我认为重要的东西）

分组密码（Block ciphers）

      分组密码与流密码的主要区别为，分组密码每次对一个n长的数据块进行处理，不论明文的长度有多长，每次对一个明文块进行相同的变换得到密文。分组算法所产生的密文块不依赖于之前的明密文信息，只跟其对应的明文块有关。最为著名的分组密码为AES算法，宏观运行流程如下图所示。
                                                 ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70][]

分组密码的安全性定义

分组密码的安全性定义要求能够抵抗积极的黑盒敌手：

      黑盒敌手定义为该敌手仅仅只能控制输入Input与接受输出Output，黑盒敌手不能看到加解密的具体过程，但是该敌手可以适应性的询问加解密算法，根据其获得的输出适应性的进行下一次询问。
      安全性要求对于黑盒敌手来说，其不能区分询问获得的密文与一个随机置换得到密文的区别，也可以说经过加密得到的密文与一个随机置换得到的密文是计算不可区分的。

分组密码安全的形式化定义：

     构造黑盒敌手攻击游戏如下图所示：
                                                ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 1][]
     和语义安全定义类似，定义两个实验Exp0-1。实验0为挑战者按照诚实执行加密算法，将加密结果返回给敌手。实验1为挑战者选择一个随机的置换，将随机置换后得到的密文返回给敌手。敌手的优势为：
                                         ![20210715160922402.png][]

定义这个敌手为Q-query BC adversary，敌手最多进行Q次询问。

分组密码安全性含义

1.分组密码密文是不可预测的（与随机置换不可区分）。

2.分组密码密文是能够抵抗秘钥恢复攻击的（因为不可预测）。

3.分组密码密文能够有效抵抗穷举搜索秘钥攻击（秘钥空间大）。

随机置换的高效实现方式

    挑战者实现一个随机置换是一个非常低效的方式，尽管在理论上看来只需要随机选择一个置换即可，但是以AES算法为例，一个随机置换的操作长度至少需要2^128比特长度。所以设计一种高效的随机数置换实现方式在实践过程中非常重要。

具体策略如下：

                      ![20210715162357178.png][]

如果敌手之前询问过该明文，则直接返回之前回复的值，如果敌手之前没有询问过该明文，则直接从置换空间中找一个没有使用过的值进行回复，这种方法既可以保证挑战者实现了一个函数，也保证该函数是一个置换，这种实现方式与可证明安全技术的“随机语言机”技术是相同的。

证明分组密码是语义安全的

安全性定理描述如下：

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 2

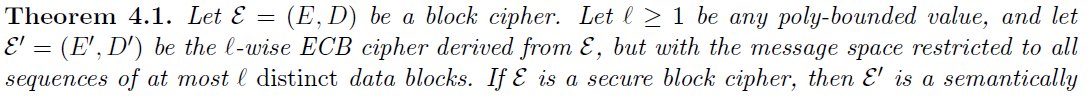
如果分组加密方案是BC安全（黑盒安全的），那么l-分组加密就是语义安全的，对于任意能够赢得语义安全游戏的敌手A，存在一个BC敌手B能够赢得黑盒安全游戏。

证明主要思路如下图所示，如果存在一个能够赢得语义安全的敌手A，那么黑盒敌手可以调用敌手A来攻击黑盒安全挑战者，所以构造一个规约算法，使用黑盒B作为A的挑战者角色，B企图通过调用A来完成黑盒攻击游戏，然而，该方案是黑盒安全的，所以无法攻击成功，所以A不能赢得该游戏。即为证明语义安全敌手优势与黑盒敌手优势相当，而黑盒敌手的优势可以忽略，所以l-分组方案是安全的。

                         ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 3][]

证明过程：

          第一步，明确证明目标：SS敌手优势 == BC敌手优势
                      ![20210715171828107.png][]
          第二步，分别建立等式两端内容：
                 2-1 构建语义安全游戏Game0与语义安全优势如下：
                       ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 4][]
                2-2 构建语义安全游戏Game1与黑盒敌手优势如下：
                        ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 5][]                                        这里需要注意，此时敌手A无法区分是与语义安全挑战者与其交互还是黑盒挑战者与其交互，因为我们可以使用黑盒敌手B调用敌手A，使用B来作为A的挑战者角色。因为如此，我们才可以使用这两个游戏得到黑盒敌手的优势：
                                                 ![20210715173728180.png][]
            第三步，构造理想化实验Game2与理想化实验的敌手优势如下：
                     ![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ptcmxpbnV4_size_16_color_FFFFFF_t_70 6][]
                       在Game2中，我们知道，敌手的输出是独立的，概率为二分之一，综合上述内容，证明目标等式成立，证明完成。