机器学习—线性回归
花了2天时间看了吴恩达老师的机器学习算法的第一章,收获很多,在网易云课堂上可看,虽然是英文版的,且偏向于理论,故在此记录下学习收获和代码实现。
1.y=kx+b的线性回归
1.1导包与前序工作
import numpy as npimport matplotlib.pyplot as plt# 1. 导入数据(两列)data=np.genfromtxt('csv/data.csv', delimiter=',')x_data=data[:,0]y_data=data[:,1]plt.scatter(x_data,y_data)plt.show()# 学习率learning rate(步长)、截距、斜率、最大迭代次数lr=0.0005b=1k=0epochs=5000
csv数据集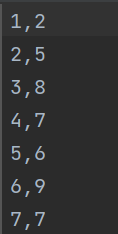
1.2代价函数
这里的代价函数为两点之间的距离差距的平方
def compute_error(b,k,x_data,y_data):totalError=0for i in range(0,len(x_data)):totalError+=(y_data[i]-(k*x_data[i]+b))**2return totalError/float(len(x_data))
1.3 梯度下降算法
记录一个理解了好久才理解的点
1.梯度下降中,如下代码
k_grad+= -(1/m)x_data[j](y_data[j]-((k*x_data[j])+b))
是根据微积分中的偏导数求出来的,公式为
2.迭代更新时应该同时更新,而不是先更新k,再更新b
def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):# 总数据量m=float(len(x_data))# 迭代epochs次for i in range(epochs):b_grad=0k_grad=0for j in range(0,len(x_data)):b_grad+= -(1/m)*(y_data[j]-((k*x_data[j])+b))k_grad+= -(1/m)*x_data[j]*(y_data[j]-((k*x_data[j])+b))# 更新b和kb= b-(lr*b_grad)k= k-(lr*k_grad)# 每迭代500次,输出一次图像和数据if i%500 ==0:print('epochs:',i)print('b:',b,'k:',k)print('error:',compute_error(b,k,x_data,y_data),)plt.plot(x_data,y_data,'b')plt.plot(x_data,k*x_data+b,'r')plt.show()return b,k
1.4启动函数
gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
上面这些代码是看了某个csdn的大佬学过来的,所以可能有雷同,修改成了3元的,思路差不多
2 z=k1x+k2y+c的线性回归
# 三元 z=b+k1x+k2yimport numpy as npimport matplotlib.pyplot as plt# 1. 导入数据(两列)data=np.genfromtxt('csv/data2.csv', delimiter=',')x_data=data[:,0] # 冒号先后:从第0行取到最后一行,逗号后面0:只要第一列y_data=data[:,1]z_data=data[:,2]# 学习率learning rate(步长)、截距、斜率、最大迭代次数lr=0.0005b=1k1=0k2=0epochs=100000# 2. 代价函数(最小二乘法):该函数只返回一个值def compute_error(b,k1,k2,x_data,y_data,z_data):totalError=0for i in range(0,len(x_data)):totalError+=(z_data[i]-(k1*x_data[i]+k2*y_data[i]+b))**2return totalError/float(len(x_data))# 3. 梯度降低算法函数def gradient_descent_runner(x_data,y_data,z_data,b,k1,k2,lr,epochs):# 总数据量m=float(len(x_data))# 迭代epochs次for i in range(epochs):b_grad=0k1_grad=0k2_grad=0for j in range(0,len(x_data)):b_grad+= -(1/m)*(z_data[j]-((k1*x_data[j])+(k2*y_data[j])+b))k1_grad+= -(1/m)*x_data[j]*(z_data[j]-((k1*x_data[j])+(k2*y_data[j])+b))k2_grad+= -(1/m)*y_data[j]*(z_data[j]-((k1*x_data[j])+(k2*y_data[j])+b))# 更新b和kb= b-(lr*b_grad)k1= k1-(lr*k1_grad)k2= k2-(lr*k2_grad)# 每迭代500次,输出一次图像和数据if i%5000 ==0:print('epochs:',i)print('b:',b,'k1:',k1,'k2:',k2)print('error:',compute_error(b,k1,k2,x_data,y_data,z_data),)return b,k1,k2gradient_descent_runner(x_data,y_data,z_data,b,k1,k2,lr,epochs)
数据集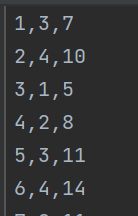
记录两个学习到的点
1.当特征值比较相似的时候,梯度下降收敛比较快,如果两个特征值相差过于大,可以使用特征缩放的方式来解决这个问题,譬如k1为[1,5],k2为[1000,2000],
可都缩放为[-1,1]这样。
2.学习率不应该过大。
刚刚考研上岸的准研究生,刚刚涉猎,如有不对,感谢指出。































还没有评论,来说两句吧...