leetcode 221. Maximal Square | 221. 最大正方形（优化的暴力解法+动态规划解法）-蒲公英云

题目

https://leetcode.com/problems/maximal-square/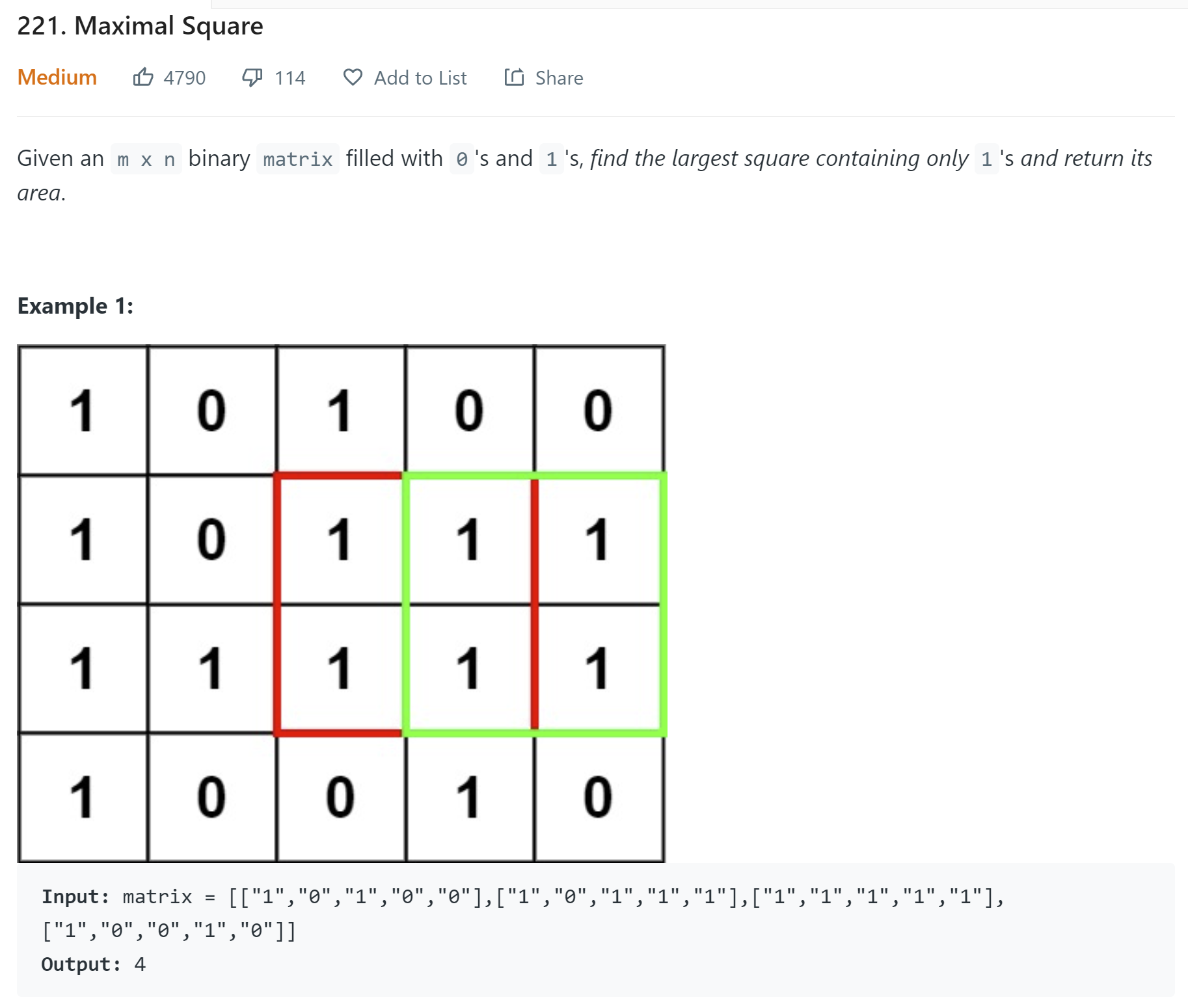
在这里插入图片描述

题解

方法1：最暴力解 O((m*n)^2)

在这里插入图片描述

public class Solution { 
    public int maximalSquare(char[][] matrix) { 
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int maxsqlen = 0;
        for (int i = 0; i < rows; i++) { 
            for (int j = 0; j < cols; j++) { 
                if (matrix[i][j] == '1') { 
                    int sqlen = 1;
                    boolean flag = true;
                    while (sqlen + i < rows && sqlen + j < cols && flag) { 
                        for (int k = j; k <= sqlen + j; k++) { 
                            if (matrix[i + sqlen][k] == '0') { 
                                flag = false;
                                break;
                            }
                        }
                        for (int k = i; k <= sqlen + i; k++) { 
                            if (matrix[k][j + sqlen] == '0') { 
                                flag = false;
                                break;
                            }
                        }
                        if (flag)
                            sqlen++;
                    }
                    if (maxsqlen < sqlen) { 
                        maxsqlen = sqlen;
                    }
                }
            }
        }
        return maxsqlen * maxsqlen;
    }
}

方法2：优化的暴力解法 O((m^2)*n)

在这里插入图片描述

虽然时间复杂度相同，但本代码没有实现上述“只看4个点”，此处待改进…

class Solution { 
    public int maximalSquare(char[][] matrix) { 
        int[][] right = new int[matrix.length][matrix[0].length]; // 向右有多少个连续的1
        int[][] down = new int[matrix.length][matrix[0].length]; // 向下有多少个连续的1
        // right
        for (int i = matrix.length - 1; i >= 0; i--) { 
            int count = 0;
            for (int j = matrix[0].length - 1; j >= 0; j--) { 
                if (matrix[i][j] == '0') count = 0;
                else count++;
                right[i][j] = count;
            }
        }
        // down
        for (int i = matrix[0].length - 1; i >= 0; i--) { 
            int count = 0;
            for (int j = matrix.length - 1; j >= 0; j--) { 
                if (matrix[j][i] == '0') count = 0;
                else count++;
                down[j][i] = count;
            }
        }
        // check
        int area = 0;
        for (int i = 0; i < matrix.length; i++) { 
            for (int j = 0; j < matrix[0].length; j++) { 
                if (right[i][j] > 0) { 
                    int square = right[i][j]; // 正方形最大边长
                    for (int k = 0; k < right[i][j]; k++) { 
                        square = Math.min(square, down[i][j + k]); // 最大边长要取min 因为受向下连续1个数的限制
                        area = Math.max(area, Math.min((k + 1) * (k + 1), square * square)); // 最大面积要取min 因为受到起点k的距离的限制
                    }
                }
            }
        }
        return area;
    }
}

在这里插入图片描述

附：左神算法配套代码，实现了上述“只看4个点”，供参考。

package chapter_8_arrayandmatrix;
public class Problem_21_MaxOneBorderSize { 
    public static void setBorderMap(int[][] m, int[][] right, int[][] down) { 
        int r = m.length;
        int c = m[0].length;
        if (m[r - 1][c - 1] == 1) { 
            right[r - 1][c - 1] = 1;
            down[r - 1][c - 1] = 1;
        }
        for (int i = r - 2; i != -1; i--) { 
            if (m[i][c - 1] == 1) { 
                right[i][c - 1] = 1;
                down[i][c - 1] = down[i + 1][c - 1] + 1;
            }
        }
        for (int i = c - 2; i != -1; i--) { 
            if (m[r - 1][i] == 1) { 
                right[r - 1][i] = right[r - 1][i + 1] + 1;
                down[r - 1][i] = 1;
            }
        }
        for (int i = r - 2; i != -1; i--) { 
            for (int j = c - 2; j != -1; j--) { 
                if (m[i][j] == 1) { 
                    right[i][j] = right[i][j + 1] + 1;
                    down[i][j] = down[i + 1][j] + 1;
                }
            }
        }
    }
    public static int getMaxSize(int[][] m) { 
        int[][] right = new int[m.length][m[0].length];
        int[][] down = new int[m.length][m[0].length];
        setBorderMap(m, right, down);
        for (int size = Math.min(m.length, m[0].length); size != 0; size--) { 
            if (hasSizeOfBorder(size, right, down)) { 
                return size;
            }
        }
        return 0;
    }
    public static boolean hasSizeOfBorder(int size, int[][] right, int[][] down) { 
        for (int i = 0; i != right.length - size + 1; i++) { 
            for (int j = 0; j != right[0].length - size + 1; j++) { 
                if (right[i][j] >= size && down[i][j] >= size
                        && right[i + size - 1][j] >= size
                        && down[i][j + size - 1] >= size) { 
                    return true;
                }
            }
        }
        return false;
    }
    public static int[][] generateRandom01Matrix(int rowSize, int colSize) { 
        int[][] res = new int[rowSize][colSize];
        for (int i = 0; i != rowSize; i++) { 
            for (int j = 0; j != colSize; j++) { 
                res[i][j] = (int) (Math.random() * 2);
            }
        }
        return res;
    }
    public static void printMatrix(int[][] matrix) { 
        for (int i = 0; i != matrix.length; i++) { 
            for (int j = 0; j != matrix[0].length; j++) { 
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }
    public static void main(String[] args) { 
        int[][] matrix = generateRandom01Matrix(7, 8);
        printMatrix(matrix);
        System.out.println(getMaxSize(matrix));
    }
}

方法3：动态规划

思路来源：leetcode 官方题解
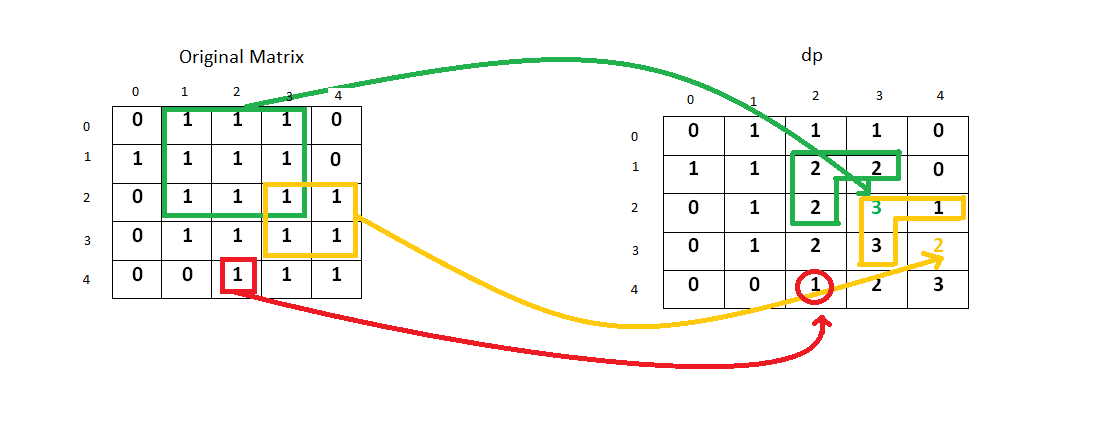
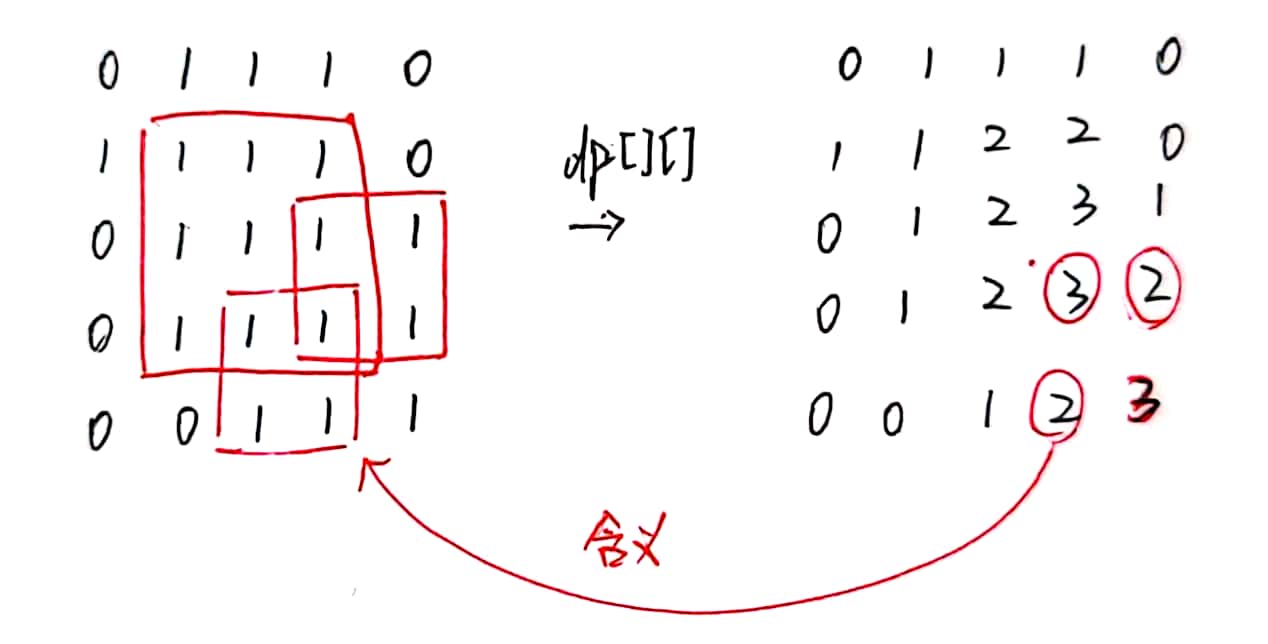
在这里插入图片描述

在这里插入图片描述

动态规划最重要的就是想清楚 d[i,j] 代表着什么，这个太重要了。

这道题中的 d[i, j] 代表的是，以坐标点(i,j) 为右下角的最大正方形，如果说你的 d[i,j] 是想这个区域中最大的正方形，那可就麻烦太多了。

官方题解代码：

public class Solution { 
    public int maximalSquare(char[][] matrix) { 
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int[][] dp = new int[rows + 1][cols + 1];
        int maxsqlen = 0;
        for (int i = 1; i <= rows; i++) { 
            for (int j = 1; j <= cols; j++) { 
                if (matrix[i-1][j-1] == '1'){ 
                    dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
                    maxsqlen = Math.max(maxsqlen, dp[i][j]);
                }
            }
        }
        return maxsqlen * maxsqlen;
    }
}

方法4：动态规划的优化解法

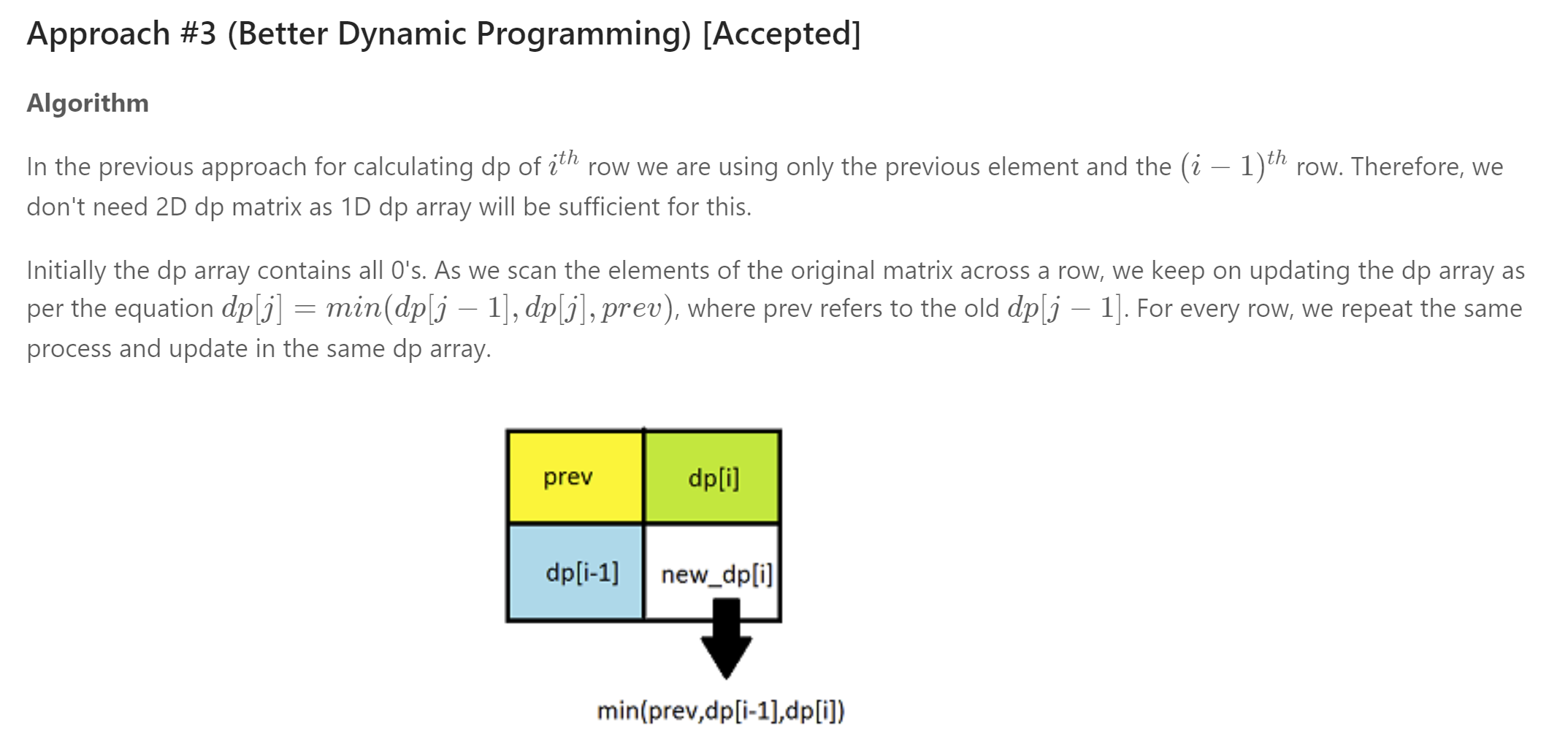
在这里插入图片描述

public class Solution { 
    public int maximalSquare(char[][] matrix) { 
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int[] dp = new int[cols + 1];
        int maxsqlen = 0, prev = 0;
        for (int i = 1; i <= rows; i++) { 
            for (int j = 1; j <= cols; j++) { 
                int temp = dp[j];
                if (matrix[i - 1][j - 1] == '1') { 
                    dp[j] = Math.min(Math.min(dp[j - 1], prev), dp[j]) + 1;
                    maxsqlen = Math.max(maxsqlen, dp[j]);
                } else { 
                    dp[j] = 0;
                }
                prev = temp;
            }
        }
        return maxsqlen * maxsqlen;
    }
}