leetcode 279. Perfect Squares | 279. 完全平方数（动态规划，Java）-蒲公英云

leetcode 279. Perfect Squares | 279. 完全平方数（动态规划，Java）

题目

https://leetcode.com/problems/perfect-squares/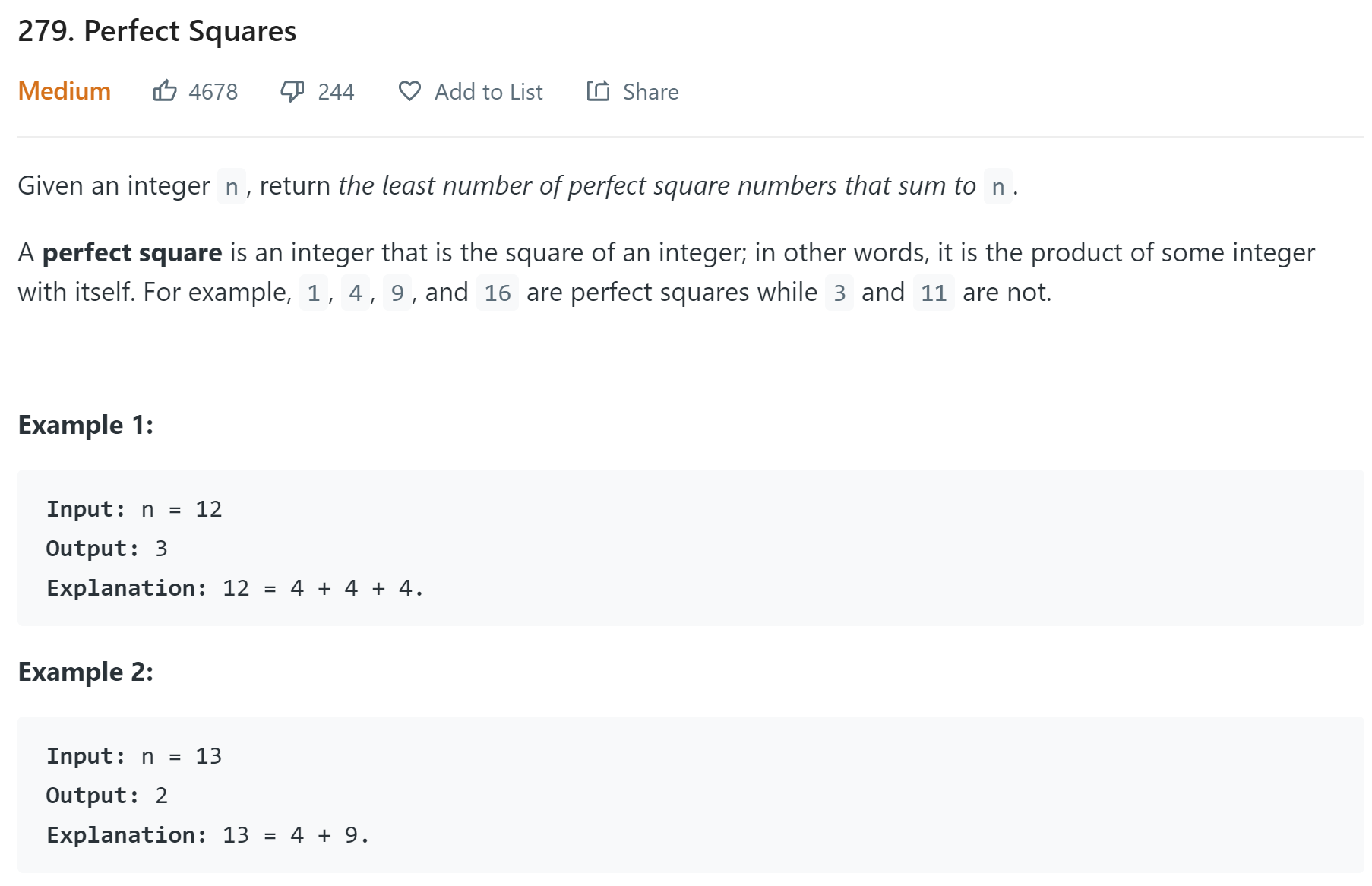
在这里插入图片描述

题解：动态规划

参考：【宫水三叶】详解完全背包一维空间优化推导（附背包问题攻略）

首先初始化长度为 n+1 的数组 dp，每个位置都为 0
如果 n 为 0，则结果为 0
对数组进行遍历，下标为 i，每次都将当前数字先更新为最大的结果，即 dp[i]=i，比如 i=4，最坏结果为 4=1+1+1+1 即为 4 个数字
状态转移方程为：dp[i] = MIN(dp[i], dp[i - j * j] + 1)，i 表示当前数字，j*j 表示平方数，实际上是 dp[i] = Math.min(dp[i], dp[i - j * j] + dp[j * j]) 的简化版，因为 dp[j * j] 必然是 1

时间复杂度：O(n∗sqrt(n))，其中 sqrt 为平方根

class Solution {

public int numSquares(int n) { 
    int[] dp = new int[n + 1];
    for (int i = 0; i <= n; i++) { 
        dp[i] = i;
        for (int j = 1; i - j * j >= 0; j++) { 
            // dp[i] = Math.min(dp[i], dp[i - j * j] + dp[j * j]);
            dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}