【论文阅读】Multi-hop Reading Comprehension through Question Decomposition and Rescoring
Multi-hop Reading Comprehension through Question Decomposition and Rescoring
论文:https://arxiv.org/abs/1906.02916
代码:https://github.com/shmsw25/DecompRC
任务
多跳阅读理解(RC)需要在几个段落中进行推理和汇总。本文提出了将一个组合式问题分解为更简单的子问题的多跳阅读理解系统,似的这些分解的子问题可以由现成的单跳阅读模型来回答。由于这种分解的注释代价很高,本文将子问题的生成重塑为一个跨度预测问题,来生成类似于人类提出的问题。
多跳问题分解为单跳子问题示例:

方法(模型)
本文提出了一种重新评分的方法,从不同的可能的分解中获得答案,并对每个分解的答案重新评分,以决定最终的答案,而不是一开始就决定分解的答案。
DECOMPRC模型实现方法:
- 首先,DECOMPRC根据跨度预测,将原始的多跳问题按照几个推理类型平行地分解成几个单跳的子问题。
- 然后,对于每个推理类型,DECOMPRC利用单跳阅读理解模型来回答每个子问题,并根据推理类型来组合答案。
- 最后,DECOMPRC利用了分解得分数来判断哪个分解是最合适的,并将该分解的答案输出为最终答案。
示例:

推理类型:bridging, intersection and comparison
HotpotQA数据集中推理类型分布。

Span Prediction for Sub-question Generation
训练 P o i n t e r c Pointer_c Pointerc模型,将一个问题映射成 c c c个点,通过映射生成的点来收集注释,随后将这些点用于为每个推理类型组成子问题。
S = [ s 1 , . . . , s n ] S = [s_1, . . . , s_n] S=[s1,…,sn]:表示句子中的n个单词。
使用BERT编码输入序列S:
U = B E R T ( S ) ∈ R n × h U = BERT(S) ∈ R^{n×h} U=BERT(S)∈Rn×h
n是输入句子单词个数
h是编码器的输出尺寸
计算每个映射点的概率:
i n d 1 , . . . , i n d c = a r g m a x i 1 < < . . . < < i c Π j = 1 c P ( i j = = i n d j ) ind_1, . . . , ind_c= \underset{i_1<<…<<i_c} {argmax}\Pi^c_{j=1}P(i_j==ind_j) ind1,…,indc=i1<<…<<icargmaxΠj=1cP(ij==indj)
使用single-hop RC model回答划分的子问题,预测4种类型问题的概率,进行下一步问题回答。
[ y i s p a n ; y i y e s ; y i n o ; y i n o n e ] = m a x ( U i ) W 1 ∈ R 4 [y^{span}_ i ; y^{yes} _i ; y^{no} _i; y^{none} _i ] = max(U_i)W_1∈ R_4 [yispan;yiyes;yino;yinone]=max(Ui)W1∈R4
选定4种类型中概率较大的一个作为预测概率,对不同的问题类型,进行下一步处理。
如果是跨度问题还需要预测跨度的区间。
p i s t a r t = s o f t m a x ( U i W s t a r t ) ∈ R n p^{start}_ i = softmax(U_iW_{start}) ∈ R_n pistart=softmax(UiWstart)∈Rn
p i e n d = s o f t m a x ( U i W e n d ) ∈ R n p^{end}_ i = softmax(U_iW_{end}) ∈ R_n piend=softmax(UiWend)∈Rn
数据集
HotpotQA数据集
Distractor setting和Full wiki setting
性能水平&结论
实验结果:
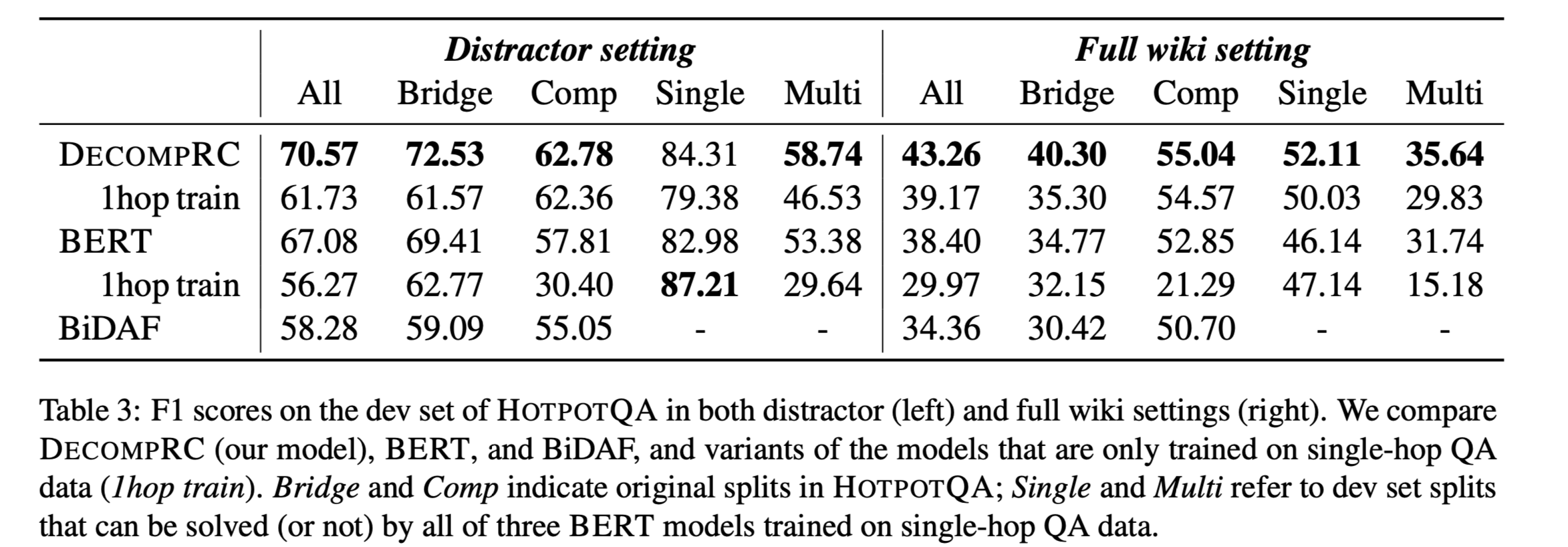
HOTPOTQA development set:
- DECOMPRC在distractor and full wiki settings 中都优于所有的基线。
- 没有经过多跳QA对训练的DECOMPRC(DECOMPRC-1hop train)在所有数据分割中都表现出不错的性能。
- 在单跳RC上训练的BERT获得了很高的F1分数(87.21)
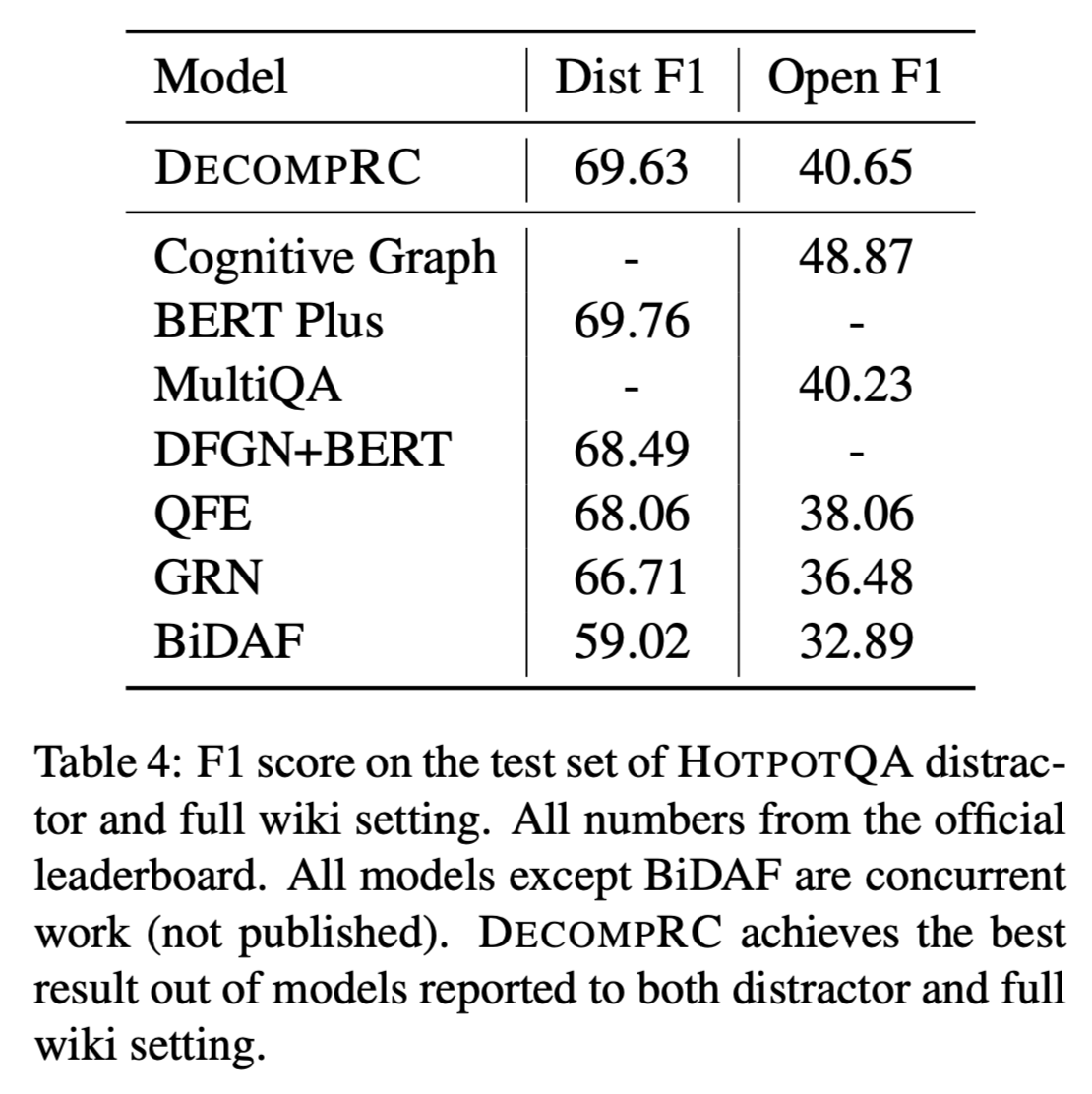
HOTPOTQA test set
distractor setting and full wiki setting
DECOMPRC在distractor setting 和 full wiki setting 相对于其他模型取得了最高的F1分数。
该方法也有一定的局限性
- 有些问题不是组合式的,但是需要隐含的多跳推理,因此不能被分解。
- 有些问题可以被分解,但每个子问题的答案在文本中并不明确存在,而是必须通过常识推理来推断。
- 所需的推理有时超出了模型设定的四种推理类型,例如算数类问题无法推理。
本文引入一种新的全局重评分方法,考虑每个分解(即子问题和它们的答案)来选择最佳的最终答案,极大地提高了整体性能。在HOTPOTQA上的实验表明,这种方法取得了最先进的结果,同时以子问题的形式为其决策提供了可解释的证据。






























还没有评论,来说两句吧...