图论方法应用

小鱼儿 2022-10-17 00:54 265阅读 0赞

声明：本博客题目和题解均来自www.acwing.com，侵权联删。

各种图论题目最合适的解法如下：
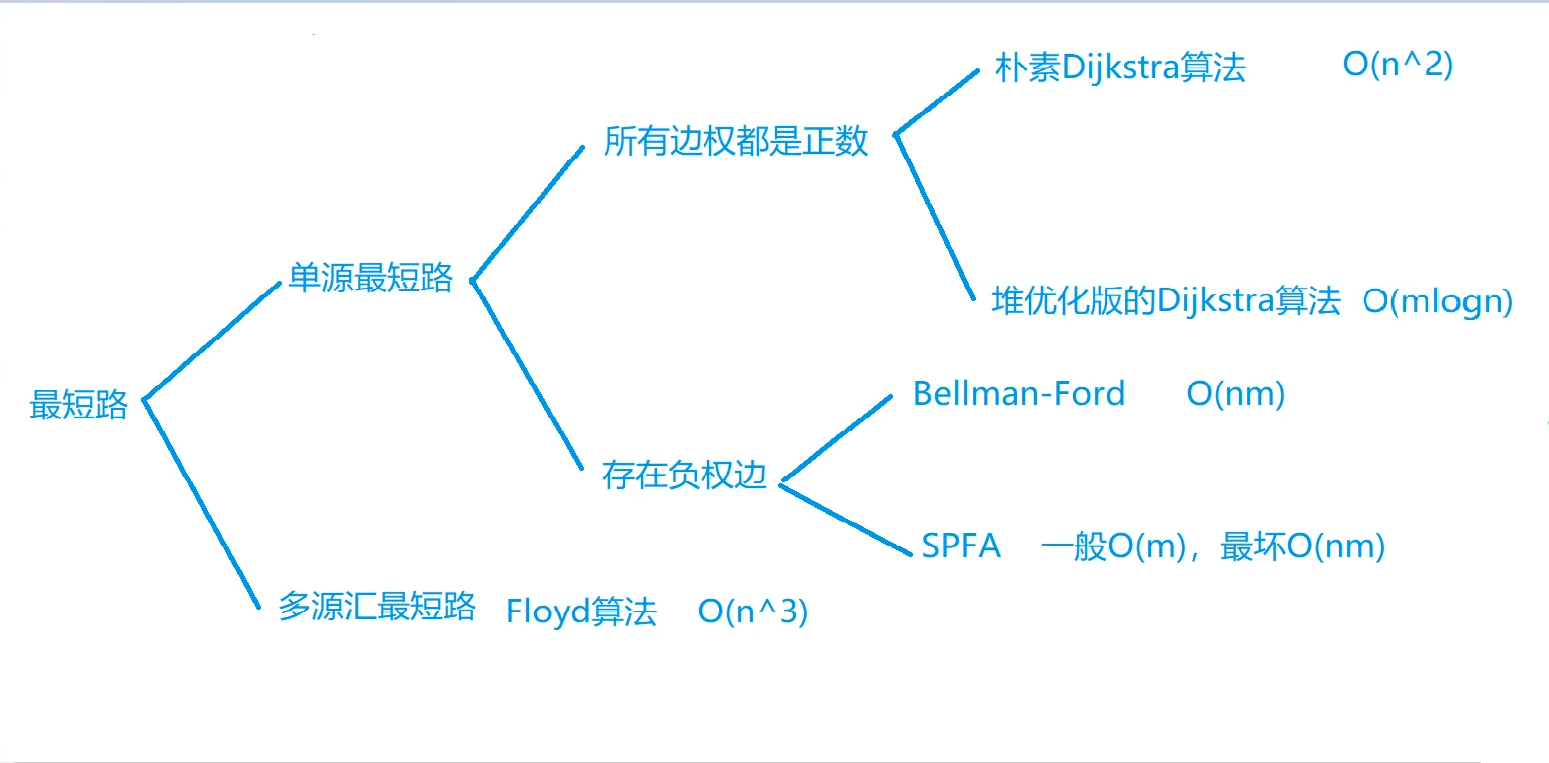
在这里插入图片描述
在这里插入图片描述

1. Dijkstra求最短路（朴素法）

给定一个 n n n 个点 m m m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n n n 号点的最短距离，如果无法从 1 号点走到 n n n 号点，则输出 −1 。

输入格式

第一行包含整数 n n n 和 m m m。
接下来 m m m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1号点到 n n n号点的最短距离。
如果路径不存在，则输出 −1。

数据范围

1 ≤ n ≤ 500 , 1≤n≤500, 1≤n≤500,
1 ≤ m ≤ 1 0 5 , 1≤m≤10^5, 1≤m≤105,
图中涉及边长均不超过10000。

输入样例：

  1. 3 3
  2. 1 2 2
  3. 2 3 1
  4. 1 3 4

输出样例：

  1. 3

标程：

  1. #include<iostream>
  2. #include<algorithm>
  3. #include<cstring>
  4. #include<cstdio>
  6. using namespace std;
  8. const int N = 510;
  10. int g[N][N];
  11. int dist[N];
  12. bool st[N];
  13. int n,m;
  15. int dijkstra()
  16. {
  18.     memset(dist,0x3f,sizeof dist);
  19.     dist[1] = 0;
  21.     for(int i = 1; i < n; i++){
  23.         int t = -1;
  24.         for(int j = 1; j <= n; j++){
  26.             if(!st[j] && (t == -1 || dist[j] < dist[t])){
  28.                 t = j;
  29.             }
  30.         }
  32.         for(int j = 1; j <= n; j++){
  34.             dist[j] = min(dist[j],dist[t]+g[t][j]);
  35.         }
  36.         st[t] = true;
  37.     }
  38.     if(dist[n] == 0x3f3f3f3f) return -1;
  39.     return dist[n];
  40. }
  42. int main()
  43. {
  45.     memset(g,0x3f,sizeof g);
  46.     scanf("%d%d",&n,&m);
  48.     for(int i = 0; i < m; i++){
  50.         int a,b,c;
  51.         scanf("%d%d%d",&a,&b,&c);
  52.         g[a][b] = min(g[a][b],c);
  53.     }
  55.     printf("%d",dijkstra());
  57.     return 0;
  58. }

2. Dijkstra求最短路（堆优化版）

给定一个 n n n 个点 m m m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n n n 号点的最短距离，如果无法从 1 号点走到 n n n 号点，则输出 −1 。

输入格式

第一行包含整数 n n n 和 m m m。
接下来 m m m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1号点到 n n n号点的最短距离。
如果路径不存在，则输出 −1。

数据范围

1 ≤ n , m ≤ 1.5 × 1 0 5 , 1≤n,m≤1.5×10^5 , 1≤n,m≤1.5×105,
图中涉及边长均不小于 0，且不超过 10000。

输入样例：

  1. 3 3
  2. 1 2 2
  3. 2 3 1
  4. 1 3 4

输出样例：

  1. 3

标程：

  1. #include<iostream>
  2. #include<queue>
  3. #include<cstring>
  4. #include<cstdio>
  5. #include<vector>
  7. using namespace std;
  9. typedef pair<int ,int> pii;
  11. const int N = 150010;
  13. int h[N],e[N],ne[N],w[N],idx;
  14. int dist[N];
  15. bool st[N];
  16. int n,m;
  18. void add(int a,int b,int c){
  20.     e[idx] = b;
  21.     w[idx] = c;
  22.     ne[idx] = h[a];
  23.     h[a] = idx++;
  24. }
  26. int dijkstra()
  27. {
  29.     memset(dist,0x3f,sizeof dist);
  30.     dist[1] = 0;
  32.     priority_queue<pii,vector<pii>,greater<pii>> heap;
  33.     heap.push({
  34.     0,1});
  36.     while(heap.size()){
  38.         pii t = heap.top();
  39.         heap.pop();
  41.         int ver = t.second;
  43.         if(st[ver]) continue;
  44.         st[ver] = true;
  46.         for(int i = h[ver]; i != -1; i = ne[i]){
  48.             int j = e[i];
  49.             if(dist[j] > dist[ver] + w[i]){
  51.                 dist[j] = dist[ver] + w[i];
  52.                 heap.push({
  53.     dist[j],j});
  54.             }
  55.         }
  56.     }
  57.     if(dist[n] == 0x3f3f3f3f) return -1;
  58.     return dist[n];
  59. }
  61. int main()
  62. {
  64.     memset(h,-1,sizeof h);
  65.     scanf("%d%d",&n,&m);
  66.     for(int i = 0; i < m; i++){
  68.         int a,b,c;
  69.         scanf("%d%d%d",&a,&b,&c);
  70.         add(a,b,c);
  71.     }
  72.     printf("%d",dijkstra());
  74.     return 0;
  75. }

3. 有边数限制的最短路 （bellman-ford）

给定一个 n n n 个点 m m m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出从 1 1 1 号点到 n n n 号点的最多经过 k k k 条边的最短距离，如果无法从 1 1 1 号点走到 n n n 号点，输出 impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数 n , m , k n,m,k n,m,k 。
接下来 m m m 行，每行包含三个整数 x , y , z x,y,z x,y,z，表示存在一条从点 x x x 到点 y y y 的有向边，边长为 z z z。

输出格式

输出一个整数，表示从 1 1 1 号点到 n n n 号点的最多经过 k k k 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围

1 ≤ n , k ≤ 500 , 1≤n,k≤500, 1≤n,k≤500,
1 ≤ m ≤ 10000 , 1≤m≤10000, 1≤m≤10000,
任意边长的绝对值不超过 10000 10000 10000。

输入样例：

  1. 3 3 1
  2. 1 2 1
  3. 2 3 1
  4. 1 3 3

输出样例：

  1. 3

标程：

  1. #include<iostream>
  2. #include<cstring>
  3. #include<cstdio>
  4. #include<algorithm>
  6. using namespace std;
  8. const int N = 510,M = 1e4+10;
  10. struct Edge
  11. {
  13.     int a,b,c;
  14. }edges[M];
  16. int n,m,k;
  17. int dist[N],last[N];
  19. void bellman_ford()
  20. {
  22.     memset(dist,0x3f,sizeof dist);
  23.     dist[1] = 0;
  24.     for(int i = 0; i < k; i++){
  26.         memcpy(last,dist,sizeof dist);
  27.         for(int j = 0; j < m; j++){
  29.             auto e = edges[j];
  30.             dist[e.b] = min(dist[e.b],last[e.a]+e.c);
  31.         }
  32.     }
  33. }
  35. int main()
  36. {
  38.     cin >> n >> m >> k;
  39.     for(int i = 0; i < m; i++){
  41.         int a,b,c;
  42.         scanf("%d%d%d",&a,&b,&c);
  43.         edges[i] = {
  44.     a,b,c};
  45.     }
  46.     bellman_ford();
  48.     if(dist[n] > 0x3f3f3f3f/2) puts("impossible");
  49.     else printf("%d\n",dist[n]);
  51.     return 0;
  52. }

4. spfa求最短路

给定一个 n n n 个点 m m m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出 1 1 1 号点到 n n n 号点的最短距离，如果无法从 1 1 1 号点走到 n n n 号点，则输出 impossible。

数据保证不存在负权回路。

输入格式

第一行包含三个整数 n , m n,m n,m 。
接下来 m m m 行，每行包含三个整数 x , y , z x,y,z x,y,z，表示存在一条从点 x x x 到点 y y y 的有向边，边长为 z z z。

输出格式

输出一个整数，表示 1 1 1 号点到 n n n 号点的最短距离。
如果路径不存在，则输出 impossible。

数据范围

1 ≤ n , m ≤ 1 0 5 , 1≤n,m≤10^5, 1≤n,m≤105,
图中涉及边长绝对值均不超过 10000 10000 10000。

输入样例：

  1. 3 3
  2. 1 2 5
  3. 2 3 -3
  4. 1 3 4

输出样例：

  1. 2
  3. #include<iostream>
  4. #include<cstring>
  5. #include<algorithm>
  6. #include<cstdio>
  7. #include<queue>
  9. using namespace std;
  11. const int N = 1e5+10;
  13. int n,m;
  14. int h[N],w[N],e[N],ne[N],idx;
  15. int dist[N];
  16. bool st[N];
  18. void add(int a,int b,int c){
  20.     e[idx] = b;
  21.     w[idx] = c;
  22.     ne[idx] = h[a];
  23.     h[a] = idx++;
  24. }
  26. int spfa()
  27. {
  29.     memset(dist,0x3f,sizeof dist);
  30.     dist[1] = 0;
  32.     queue<int> q;
  33.     q.push(1);
  34.     st[1] = true;
  36.     while(!q.empty()){
  38.         int t = q.front();
  39.         q.pop();
  40.         st[t] = false;
  42.         for(int i = h[t]; i != -1; i = ne[i]){
  44.             int j = e[i];
  45.             if(dist[j] > dist[t]+w[i]){
  47.                 dist[j] = dist[t] + w[i];
  48.                 if(!st[j]){
  50.                     st[j] = true;
  51.                     q.push(j);
  52.                 }
  53.             }
  54.         }
  55.     }
  56.     return dist[n];
  57. }
  59. int main()
  60. {
  62.     scanf("%d%d",&n,&m);
  63.     memset(h,-1,sizeof h);
  64.     for(int i = 0; i < m; i++){
  66.         int a,b,c;
  67.         scanf("%d%d%d",&a,&b,&c);
  68.         add(a,b,c);
  69.     }
  70.     int t = spfa();
  72.     if(t == 0x3f3f3f3f) puts("impossible");
  73.     else printf("%d\n",t);
  75.     return 0;
  76. }

5. spfa判断负环

给定一个 n n n 个点 m m m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路。

输入格式

第一行包含整数 n n n 和 m m m。

接下来 m m m 行每行包含三个整数 x , y , z x,y,z x,y,z，表示存在一条从点 x x x 到点 y y y 的有向边，边长为 z z z。

输出格式

如果图中存在负权回路，则输出 Yes，否则输出 No。

数据范围

1 ≤ n ≤ 2000 , 1≤n≤2000, 1≤n≤2000,
1 ≤ m ≤ 10000 , 1≤m≤10000, 1≤m≤10000,
图中涉及边长绝对值均不超过 10000 10000 10000。

输入样例：

  1. 3 3
  2. 1 2 -1
  3. 2 3 4
  4. 3 1 -4

输出样例：

  1. Yes

标程：

  1. #include<iostream>
  2. #include<queue>
  3. #include<cstring>
  4. #include<algorithm>
  6. using namespace std;
  8. const int N = 2e3+10,M = 1e4+10;
  10. int n,m;
  11. int h[N],e[M],w[M],ne[M],idx;
  12. int dist[N],cnt[N];
  13. bool st[N];
  15. void add(int a,int b,int c){
  17.     e[idx] = b;
  18.     w[idx] = c;
  19.     ne[idx] =h[a];
  20.     h[a] = idx++;
  21. }
  23. bool spfa(){
  25.     queue<int> q;
  26.     for(int i = 1; i <= n; i++){
  28.         q.push(i);
  29.         st[i] = true;
  30.     }
  31.     while(q.size()){
  33.         int t = q.front();
  34.         q.pop();
  35.         st[t] = false;
  37.         for(int i = h[t]; i != -1; i = ne[i]){
  39.             int j = e[i];
  40.             if(dist[j] > dist[t] + w[i]){
  42.                 dist[j] = dist[t] + w[i];
  43.                 cnt[j] = cnt[t] + 1;
  44.                 if(cnt[j] >= n) return true;
  45.                 if(!st[j]){
  47.                     st[j] = true;
  48.                     q.push(j);
  49.                 }
  50.             }
  51.         }
  52.     }
  53.     return false;
  54. }
  56. int main()
  57. {
  59.     scanf("%d%d",&n,&m);
  60.     memset(h,-1,sizeof h);
  61.     for(int i = 0; i < m; i++){
  63.         int a,b,c;
  64.         scanf("%d%d%d",&a,&b,&c);
  65.         add(a,b,c);
  66.     }
  67.     if(spfa()) puts("Yes");
  68.     else puts("No");
  70.     return 0;
  71. }

6. Floyd求最短路

给定一个 n 个点 m条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 k个询问，每个询问包含两个整数 x 和 y，表示查询从点 x 到点 y的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式

第一行包含三个整数 n,m,k。

接下来 m行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

接下来 k行，每行包含两个整数 x,y，表示询问点 x 到点 y的最短距离。

输出格式

共 k行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围

1 ≤ n ≤ 200 , 1≤n≤200, 1≤n≤200,
1 ≤ k ≤ n 2 1≤k≤n^2 1≤k≤n2
1 ≤ m ≤ 20000 , 1≤m≤20000, 1≤m≤20000,
图中涉及边长绝对值均不超过 10000 10000 10000。

输入样例：

  1. 3 3 2
  2. 1 2 1
  3. 2 3 2
  4. 1 3 1
  5. 2 1
  6. 1 3

输出样例：

  1. impossible
  2. 1

标程：

  1. #include<iostream>
  2. #include<cstring>
  3. #include<cstdio>
  4. #include<algorithm>
  6. using namespace std;
  8. const int N = 210,INF = 1e9;
  10. int n,m,t;
  11. int g[N][N];
  13. void floyd()
  14. {
  16.     for(int k = 1; k <= n; k++){
  18.         for(int i = 1; i <= n; i++){
  20.             for(int j = 1; j <= n; j++){
  22.                 g[i][j] = min(g[i][j],g[i][k]+g[k][j]);
  23.             }
  24.         }
  25.     }
  26. }
  28. int main()
  29. {
  31.     scanf("%d%d%d",&n,&m,&t);
  33.     for(int i = 1; i <= n; i++){
  35.         for(int j = 1; j <= n; j++){
  37.             if(i == j) g[i][j] = 0;
  38.             else g[i][j] = INF;
  39.         }
  40.     }
  42.     for(int i = 0; i < m; i++){
  44.         int a,b,c;
  45.         scanf("%d%d%d",&a,&b,&c);
  46.         g[a][b] = min(g[a][b],c);
  47.     }
  49.     floyd();
  51.     for(int i = 0; i < t; i++){
  53.         int a,b;
  54.         scanf("%d%d",&a,&b);
  55.         if(g[a][b] > INF/2) puts("impossible");
  56.         else printf("%d\n",g[a][b]);
  57.     }
  59.     return 0;
  60. }

7. Prim算法求最小生成树

给定一个 n n n个点 m m m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E)，其中 V V V 表示图中点的集合， E E E 表示图中边的集合， n = ∣ V ∣ ， m = ∣ E ∣ n=|V|，m=|E| n=∣V∣，m=∣E∣。

由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。

输入格式

第一行包含两个整数 n n n 和 m m m。

接下来 m行，每行包含三个整数 u , v , w u,v,w u,v,w，表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

1 ≤ n ≤ 500 , 1≤n≤500, 1≤n≤500,
1 ≤ m ≤ 105 , 1≤m≤105, 1≤m≤105,
图中涉及边的边权的绝对值均不超过 10000 10000 10000。

输入样例：

  1. 4 5
  2. 1 2 1
  3. 1 3 2
  4. 1 4 3
  5. 2 3 2
  6. 3 4 4

输出样例：

  1. 6

标程：

  1. #include<iostream>
  2. #include<cstdio>
  3. #include<algorithm>
  4. #include<cstring>
  6. using namespace std;
  8. const int N = 510,INF = 0x3f3f3f3f;
  10. int n,m;
  11. int g[N][N];
  12. int dist[N];
  13. bool st[N];
  15. int prime()
  16. {
  18.     memset(dist,0x3f,sizeof dist);
  20.     int ans = 0;
  21.     for(int i = 0; i < n; i++){
  23.         int t = -1;
  24.         for(int j = 1; j <= n; j++){
  26.             if(!st[j] && (t == -1 || dist[t] > dist[j]))
  27.                 t = j;
  28.         }
  30.         if(i && dist[t] == INF) return INF;
  32.         if(i) ans += dist[t];
  33.         st[t] = true;
  35.         for(int j = 1; j <= n; j++) dist[j] = min(dist[j],g[t][j]);
  36.     }
  38.     return ans;
  39. }
  41. int main()
  42. {
  44.     scanf("%d%d",&n,&m);
  46.     memset(g,0x3f,sizeof g);
  48.     for(int i = 0; i < m; i++){
  50.         int a,b,c;
  51.         scanf("%d%d%d",&a,&b,&c);
  52.         g[a][b] = g[b][a] = min(g[a][b],c);
  53.     }
  55.     int t = prime();
  57.     if(t == INF) printf("impossible\n");
  58.     else printf("%d\n",t);
  59. }

8. Kruskal算法求最小生成树

给定一个 n n n 个点 m m m条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E)，其中 V V V 表示图中点的集合， E E E 表示图中边的集合， n = ∣ V ∣ ， m = ∣ E ∣ n=|V|，m=|E| n=∣V∣，m=∣E∣。

由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。

输入格式

第一行包含两个整数 n n n 和 m m m。

接下来 m m m 行，每行包含三个整数 u , v , w u,v,w u,v,w，表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

1 ≤ n ≤ 1 0 5 , 1≤n≤10^5, 1≤n≤105,
1 ≤ m ≤ 2 ∗ 1 0 5 , 1≤m≤2∗10^5, 1≤m≤2∗105,
图中涉及边的边权的绝对值均不超过 1000。

输入样例：

  1. 4 5
  2. 1 2 1
  3. 1 3 2
  4. 1 4 3
  5. 2 3 2
  6. 3 4 4

输出样例：

  1. 6

标程：

  1. #include<iostream>
  2. #include<cstdio>
  3. #include<algorithm>
  5. using namespace std;
  7. const int N = 1e5+10,INF = 0x3f3f3f3f;
  9. struct Edge{
  11.     int a,b,w;
  12.     bool operator<(const Edge &W) const{
  14.         return w < W.w;
  15.     }
  16. }edges[N*2];
  18. int n,m;
  19. int p[N];
  21. int find(int x){
  23.     if(x != p[x]) return p[x] = find(p[x]);
  24.     else return p[x];
  25. }
  27. int kruskal()
  28. {
  30.     sort(edges,edges+m);
  32.     for(int i = 1; i <= n; i++) p[i] = i;
  34.     int ans = 0,cnt = 0;
  36.     for(int i = 0; i < m; i++){
  38.         int a = edges[i].a,b = edges[i].b,w = edges[i].w;
  39.         a = find(a),b = find(b);
  40.         if(a != b){
  42.             p[a] = b;
  43.             ans += w;
  44.             cnt++;
  45.         }
  46.     }
  47.     if(cnt < n-1) return INF;
  48.     else return ans;
  49. }
  51. int main()
  52. {
  54.     scanf("%d%d",&n,&m);
  55.     for(int i = 0 ; i< m; i++){
  57.         int a,b,c;
  58.         scanf("%d%d%d",&a,&b,&c);
  59.         edges[i] = {
  60.     a,b,c};
  61.     }
  63.     int t = kruskal();
  65.     if(t == INF) puts("impossible");
  66.     else printf("%d\n",t);
  67. }

发表评论

表情：
评论列表 （有 0 条评论，265人围观）

还没有评论，来说两句吧...

相关阅读

    相关 图论小总结

    图论最重要的就是怎么建图 在建图的时候主要考虑三件事情： 1.确定结点和边权 2.是否建分层图（最短路DP）？ 3.是否建拆点图（DP思想）？如果有限制条件，考虑两种情

    系统管理员系统管理员/ 0 赞/ 173 阅读

    相关 图论

    一、图的常用概念 　　1、顶点（vertex） 　　2、边（edge） 　　3、路径 　　4、无向图：顶点之间的连接没有方向 　　![1007094-201909

    柔光的暖阳◎柔光的暖阳◎/ 0 赞/ 176 阅读

    相关 论软件设计方法及其应用

    摘要： 2020年3月，本人就职的某互联网公司承担了“XXAPP电子商务系统”的开发，该项目是集团为用户提供电子商务业务，拉新促活，提高交易效率的重点项目，主要实现消费者的网

    小灰灰小灰灰/ 0 赞/ 159 阅读

    相关 图论基础

    图 图由节点和图构成； 有向图：连线有方向；不对称性； 无向图：连线无方向；是有向图的一种特殊请情况； 有权图：连线有权值； 无权图：连线无权值； 简

    柔情只为你懂柔情只为你懂/ 0 赞/ 267 阅读

    相关 图论之欧拉图

    欧拉路径/欧拉回路 欧拉路径是一条经过图中所有边且只经过一次的路径（类似于一笔画问题）； 欧拉回路的话就是起点和终点相同的欧拉路径 欧拉通路（欧拉路径）：S点到T点的

    蔚落蔚落/ 0 赞/ 282 阅读

    相关 图论方法应用

    声明：本博客题目和题解均来自www.acwing.com，侵权联删。 各种图论题目最合适的解法如下： ![在这里插入图片描述][watermark_type_ZmFu

    小鱼儿小鱼儿/ 0 赞/ 266 阅读

    相关 图论

    http://[blog.csdn.net/pipisorry/article/details/52518118][blog.csdn.net_pipisorry_articl

    清疚清疚/ 0 赞/ 380 阅读

    相关 图论算法

    Problem1一笔画问题 题目描述     给出一个图，求其欧拉回路（若没有回路，则求其欧拉路径），若不存在则输出‘No solution’ 输入     输入的第一

    妖狐艹你老母妖狐艹你老母/ 0 赞/ 389 阅读

    相关 图论 Floyd算法

    Floyd算法　　 　　时间复杂度O (n^3) 　　空间复杂度O (n^2) 用处 　　可以求任意两个点之间的最短路径长度。 　　得出的邻接矩阵存储 i 到 j 的

    青旅半醒青旅半醒/ 0 赞/ 380 阅读

    相关 图论重点复习

    一、重点概念 1、图：一个图是一个序偶（V，E），记为G=( V , E),其中： （1） V是一个有限的非空集合，称为顶点集合,其元素称为顶点或点。用|V|表示顶点

    冷不防冷不防/ 0 赞/ 1366 阅读