循环神经网络（RNN）

古城微笑少年丶 2022-10-30 15:24 453阅读 0赞

对于人类而言，以前见过的事物会在脑海中留下记忆，虽然随后记忆会慢慢消失，但是每当经过提醒，人们往往可以重拾记忆。在神经网络中也是一样，之前介绍的CNN模型都是与时间序列无关的模型，它有明显的局限性，就是只能单独的去处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。所以接下来要介绍一种在序列问题和自然语言处理等领域取得很大成功的模型——循环神经网络。

一. 循环神经网络（RNN）

具体来讲，卷积神经网络相当于人类的视觉，但是它没有记忆能力，所以它只能处理一种特定的视觉任务，没办法根据以前的来处理新的任务。那么记忆力对于网络而言到底是不是必要的呢？我们可以考虑这样一个场景，在一场电影中推断下一个时间点的场景，这个时候仅依赖于现在的情景并不够，需要依赖于前面发生的情节。对于这样一些不仅依赖于当前情况，还依赖于过去情况的问题，传统的神经网络结构无法很好的处理，所以基于记忆的网络模型是必不可少的。循环神经网络的提出便是基于记忆模型的想法，期望网络能够记住前面出现的特征，并依据特征推断后面的结果，而且整体的网络结构不断循环，因此得名为循环神经网络。

1.1 循环神经网络的基本结构

循环神经网络的基本结构非常简单，就是将网络的输出保存在一个记忆单元中，这个记忆单元和下一次的输入一起进入神经网络中。使用一个简单的两层网络作为示范，在它的基础上扩充为循环神经网络的结构，我们用下图简单表示：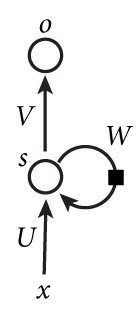
在这里插入图片描述
第一次看到的时候肯定是一脸懵逼，静下心来看看，其实也是很好理解的。如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；U是输入层到隐藏层的权重矩阵；o也是一个向量，它表示输出层的值；V是隐藏层到输出层的权重矩阵。那么，现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。

如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：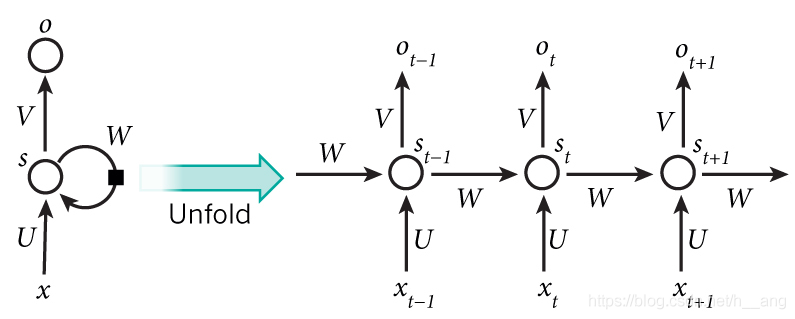
在这里插入图片描述
在这里插入图片描述
式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值作为这一次的输入的权重矩阵，f是激活函数。从上面的公式我们可以看出，循环层和全连接层的区别就是循环层多了一个权重矩阵W。

可以看到网络在输入的时候会联合记忆单元s一起作为输入，网络不仅输出结果，还会将结果保存到记忆单元中。当输入序列的顺序发生改变，网络的输出结果就会变化，这是因为记忆单元的存在，使得两个序列在顺序改变之后记忆单元中的元素也改变了，所以会影响最后的输出结果。

那么RNN到底是如何将整个序列传入网络呢？其实只需要将序列中的每个数据点x t − 1 、 x t . . . . . . 依次传入网络即可！无论序列多长，都能不断输入网络，最终得到结果。可能看到这里，大家不禁想问上图中的每个子结构是不是都是独立的权重？答案是不是的，这里各个子结构可以其实是一个共用的结构，使用了参数共享的概念。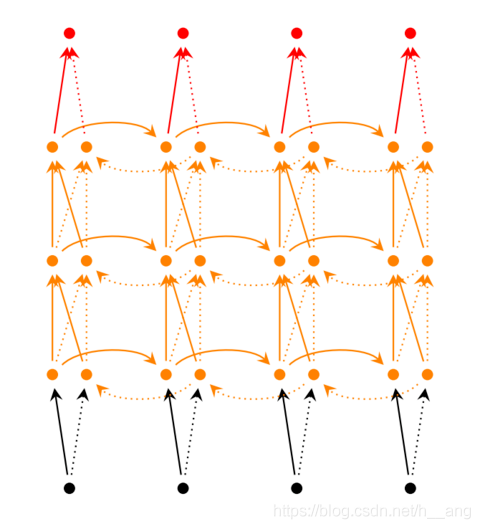
在这里插入图片描述
同时我们可以发现上面的网络都是单向的，这代表网络只能知道单侧的信息，有的时候序列的信息不只是单边有用，双边的信息对预测结果也很重要，比如语音信号，这时候就需要看到两侧信息的网络结构。这并不需要用两个循环神经网络分别从左右两边开始读取序列输入，使用一个双向的循环神经网络就可以完成这个任务，如下图：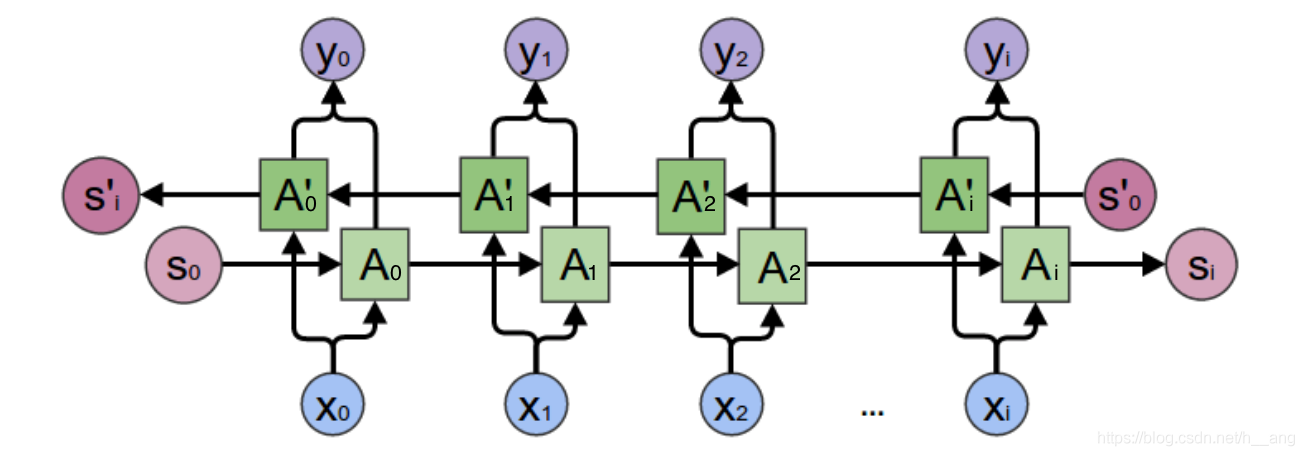
在这里插入图片描述
在这里插入图片描述

1.2 循环层的训练

针对循环层的训练，使用的是BPTT算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

  1. 前向计算每个神经元的输出值；
  2. 反向计算每个神经元的误差项值，它是误差函数E对神经元j的加权输入的偏导数；
  3. 计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。具体推导可见：https://zybuluo.com/hanbingtao/note/541458

1.3 存在的问题

根据前面介绍的内容可以了解到循环神经网络具有特别好的记忆特性，能够将记忆内容应用到当前情景下，但是随后人们发现网络的记忆能力并没有想象中那么有效。

记忆最大的问题在于它有遗忘性，我们总是更加清楚地记得最近发生的事情而遗忘很久之前发生的事情，循环神经网络也有同样的问题。如果一项任务需要依赖近期的信息来预测结果，循环神经网络往往具有比较好的特性，比如给出下面一句话“我住在中国，我会讲中文”，使用循环神经网络就能够依据前面内容中的“中国”来预测后面的“中文”。循环神经网络能够很好地解决这种短时依赖的问题。

但与对于长时依赖的问题，循环神经网络的表现就不再那么尽如人意。比如讲上一个问题的这句话拆开，在一篇的文章的开头写上“我住在中国”，希望循环神经网络在文章的末尾能够预测“我会说中文”，这时网络就没办法很好地预测这个结果，因为记忆的信息和预测位置之间的跨度太大，网络往往不能记忆这么长时间的信息，而且随着时间跨度越来越大，循环神经网络也越来越难以学习这些信息。

那么为什么循环神经网络会存在这样的问题呢？一个主要的原因是RNN在训练过程中很容易发生梯度爆炸和梯度消失，这导致训练时梯度不能在较长序列中一直传递下去，从而使得RNN无法捕捉到较长距离的影响。

在这里插入图片描述
式的β定义为矩阵的模的上界。因为上式是一个指数函数，如果t-k很大的话，会导致对应的误差项的值增加或减小的很快，着就会导致相应的梯度爆炸和梯度消失问题（取决于β大于1还是小于1）。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会受到Nan错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

  1. 合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域。
  2. 使用relu代替sigmoid和tanh作为激活函数。原理请参数考上一篇文章零基础入门深度学习(4)-卷积神经网络的激活函数一节（https://blog.csdn.net/h\_\_ang/article/details/89441492）。
  3. 使用其他结构的RNNs，比如长短时记忆网络（LTSM）和Gated Recurrent Unit（GRU），这是最流行的做法。我们将在以后的文章中介绍这两种网络。

二. 循环神经网络的PyTorch实现

2.1 标准RNN模块

先给出标准RNN的示意图，如下图所示，先来讲解PyTorch中的API。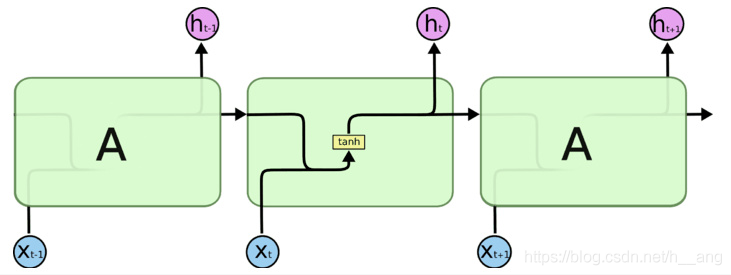
在这里插入图片描述
从上图可以看到在标准RNN的内部网络，计算公式如下：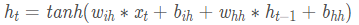
在这里插入图片描述
在PyTorch中可以使用下面两种方式去调用，分别是torch.nn.RNNCell()和torch.nn.RNN()，这两种方式的区别在于RNNCell()只能接受序列中单步的输入，且必须传入隐藏状态，而RNN()可以接受一个序列的输入，默认会传入全0的隐藏状态，也可以自己申明隐藏状态传入。

RNN()里面的参数有：

  1. 1. input_size 表示 x_{ t} 的特征维度；
  2. 2. hidden_size 表示输出 h_{ t} 的特征维度；
  3. 3. num_layers 表示网络的层数，默认是1层；
  4. 4. nonlinearity 表示非线性激活函数的选择，默认是tanh，也可以选择 relu；
  5. 5. bias 表示是否使用偏置，默认是True；
  6. 6. batch_first 这个参数是决定网络的输入维度顺序，默认网络输入是按照
  7. (seq, batch, feature) 输入的，也就是序列长度放在最前面，然后是批量，最后是特征维度，如果这个参数设置为True，那么顺序就变为 (batch, seq, feature)；
  8. 7. dropout 这个参数接受一个 0-1 的数值，会在网络中除最后一层之外的其他输出层加上 
  9. dropout层；
  10. 8. bidirectional 默认是False，如果设置为 True，就是双向循环神经网络的结构；

在这里插入图片描述
这里有几个地方要注意一下：

  • 第一个要注意的地方就是网络的输入和前面讲过的卷积神经网络不同，因为卷积神经网络的输入是将batch放在前面，而在循环神经网络中将batch放在中间，当然可以使用batch_first=True 让batch放在前面；
  • 第二个要注意的地方就是网络的输出是(seq,batch,hidden∗direction)，这里的 direction=1或者2前面也说过，如果是双向的网络结构，相当于网络从左往右计算一次，再从右往左计算一次，这样就会有两个结果，将两个结果按最后一维拼接起来，就是上面的结果；
  • 第三个要注意的地方就是隐藏状态的网络大小、输入和输出都是(layer∗direction,batch,hidden)，因为如果网络有多层，那么每一层都有一个新的记忆单元，而双向网络结构在每一层左右都会有两个不同的记忆单元，所以维度的第一维为layer*directionlayer∗direction

2.1.1 torch.nn.RNN()

  1. import torch
  2. from torch.autograd import Variable
  3. from torch import nn
  5. # 首先建立一个简单的循环神经网络：输入维度为20， 输出维度是50， 两层的单向网络
  6. basic_rnn = nn.RNN(input_size=20, hidden_size=50, num_layers=2)
  7. """ 通过 weight_ih_l0 来访问第一层中的 w_{ih}，因为输入 x_{t}是20维，输出是50维， 所以w_{ih}是一个50*20维的向量，另外要访问第二层网络可以使用 weight_ih_l1. 对于w_{hh}，可以用 weight_hh_l0来访问，而 b_{ih}则可以通过 bias_ih_l0来访问。 当然可以对它进行自定义的初始化，只需要记得它们是 Variable，取出它们的data，对它进行自定的初始化即可。 """
  8. print(basic_rnn.weight_ih_l0.size(), basic_rnn.weight_ih_l1.size(), basic_rnn.weight_hh_l0.size())
  10. # 随机初始化输入和隐藏状态
  11. toy_input = Variable(torch.randn(3, 1, 20))
  12. h_0 = Variable(torch.randn(2*1, 1, 50))
  14. print(toy_input[0].size())
  15. # 将输入和隐藏状态传入网络，得到输出和更新之后的隐藏状态，输出维度是(100, 32, 20)。
  16. toy_output, h_n = basic_rnn(toy_input, h_0)
  17. print(toy_output[-1])
  19. print(h_n)
  20. print(h_n[1])

运行结果如下：

  1. torch.Size([50, 20]) torch.Size([50, 50]) torch.Size([50, 50])
  2. torch.Size([1, 20])
  3. tensor([[-0.3125,  0.3973,  0.1015, -0.3056,  0.2984, -0.0861,  0.0475, -0.1786,
  4.          -0.1517, -0.1942, -0.5226,  0.1371,  0.3742,  0.0015,  0.4170, -0.4198,
  5.           0.0016,  0.0105, -0.2888,  0.0264,  0.0918,  0.1995,  0.3652,  0.0726,
  6.          -0.5060, -0.1590, -0.0563,  0.5157,  0.0711,  0.0323,  0.0887, -0.1204,
  7.          -0.0398,  0.3139,  0.3033, -0.2959, -0.0364, -0.1694, -0.0850,  0.1677,
  8.           0.1336,  0.3585,  0.5347,  0.1715,  0.0744, -0.0638, -0.0288,  0.2030,
  9.          -0.0331,  0.0917]], grad_fn=<SelectBackward>)
  10. tensor([[[-0.1628, -0.4115,  0.4866,  0.0894, -0.0854, -0.2157, -0.2621,
  11.           -0.5516, -0.4519,  0.0018,  0.4441, -0.3733,  0.0452,  0.2810,
  12.            0.3448, -0.7629,  0.3183, -0.2545, -0.2442, -0.1096,  0.4241,
  13.           -0.5551,  0.3997,  0.1226, -0.7918,  0.6856, -0.3279, -0.2584,
  14.            0.2747,  0.4487,  0.1052,  0.0385,  0.8092, -0.0833, -0.2083,
  15.            0.5290, -0.0484,  0.4514,  0.1635, -0.2942, -0.1331, -0.0157,
  16.           -0.1903, -0.3139,  0.3855,  0.5212, -0.5168, -0.0424, -0.1601,
  17.            0.3628]],
  19.         [[-0.3125,  0.3973,  0.1015, -0.3056,  0.2984, -0.0861,  0.0475,
  20.           -0.1786, -0.1517, -0.1942, -0.5226,  0.1371,  0.3742,  0.0015,
  21.            0.4170, -0.4198,  0.0016,  0.0105, -0.2888,  0.0264,  0.0918,
  22.            0.1995,  0.3652,  0.0726, -0.5060, -0.1590, -0.0563,  0.5157,
  23.            0.0711,  0.0323,  0.0887, -0.1204, -0.0398,  0.3139,  0.3033,
  24.           -0.2959, -0.0364, -0.1694, -0.0850,  0.1677,  0.1336,  0.3585,
  25.            0.5347,  0.1715,  0.0744, -0.0638, -0.0288,  0.2030, -0.0331,
  26.            0.0917]]], grad_fn=<StackBackward>)
  27. tensor([[-0.3125,  0.3973,  0.1015, -0.3056,  0.2984, -0.0861,  0.0475, -0.1786,
  28.          -0.1517, -0.1942, -0.5226,  0.1371,  0.3742,  0.0015,  0.4170, -0.4198,
  29.           0.0016,  0.0105, -0.2888,  0.0264,  0.0918,  0.1995,  0.3652,  0.0726,
  30.          -0.5060, -0.1590, -0.0563,  0.5157,  0.0711,  0.0323,  0.0887, -0.1204,
  31.          -0.0398,  0.3139,  0.3033, -0.2959, -0.0364, -0.1694, -0.0850,  0.1677,
  32.           0.1336,  0.3585,  0.5347,  0.1715,  0.0744, -0.0638, -0.0288,  0.2030,
  33.          -0.0331,  0.0917]], grad_fn=<SelectBackward>)

2.1.2 torch.nn.RNNCell()

RNNCell()只能接受序列中单步的输入，且必须传入隐藏状态。

  1. # 定义一个单步的rnn
  2. rnn_single = nn.RNNCell(input_size=100, hidden_size=200)
  3. # 访问其中的参数
  4. print(rnn_single.weight_hh.size())
  5. # 构造一个序列，长为6，batch是5，特征是100
  6. x = Variable(torch.randn(6, 5, 100))
  7. # 定义初始的记忆状态
  8. h_t = Variable(torch.zeros(5, 200))
  9. # 传入 rnn
  10. out = []
  11. for i in range(6):   # 通过循环6次作用在整个序列上
  12.     h_t = rnn_single(x[i], h_t)
  13.     out.append(h_t)

2.2 图片分类

循环神经网络特别适合处理序列数据，但对于图片类型的数据也不是没有办法处理，我们仍然可以用循环神经网络进行图片分类，下面以对MNIST手写数字分类为例。

首先需要将图片数据转化为一个序列数据，MNIST手写数字的图片大小是28×28，那么可以将每张图片看作是长为28的序列，序列中的每个元素的特征维度是28，这样就将图片变成了一个序列。同时考虑到循环神经网络的记忆性，所以图片从左往右输入网络的时候，网络可以记忆住前面观察到的东西，也就是说一张图片虽然被切割成了28份，但是网络能够通过记住前面的部分，同时和后面的部分结合得到最后预测数字的输出结果，所以从理论上而言是行得通的。

  1. import torch
  2. from torch.autograd import Variable
  3. from torch import nn
  4. from torch.utils.data import DataLoader
  5. from torchvision import transforms as tfs
  6. from torchvision.datasets import MNIST
  7. from datetime import datetime
  8. import numpy
  9. # 定义数据
  10. data_tf = tfs.Compose([tfs.ToTensor(), tfs.Normalize([0.5], [0.5])])
  12. train_set = MNIST('./data', train=True, transform=data_tf)
  13. test_set = MNIST('./data', train=False, transform=data_tf)
  15. train_data = DataLoader(train_set, batch_size=64, shuffle=True)
  16. test_data = DataLoader(test_set, batch_size=64, shuffle=False)
  18. # 定义模型
  19. class rnn_classify(nn.Module):
  20.     def __init__(self, in_feature=28, hidden_feature=100, num_class=10, num_layers=2):
  21.         super(rnn_classify, self).__init__()
  22.         self.rnn = nn.LSTM(input_size=in_feature, hidden_size=hidden_feature, num_layers=num_layers)   # 使用两层LSTM
  23.         self.classifier = nn.Linear(hidden_feature, num_class)      # 将最后一个rnn的输出使用全连接得到最后的分类结果
  24.     def forward(self, x):
  25.         # 先要将 维度为 (batch, 1, 28, 28)的x转换为 (28, batch, 28)
  26.         x = x.squeeze()        # (batch, 1, 28, 28)——(batch, 28, 28)
  27.         x = x.permute(2, 0, 1)     # 将最后一维放到第一维，变成(28, batch, 28)
  28.         out, _ = self.rnn(x)     # 使用默认的隐藏状态，即全0，得到的out是 (28, batch, hidden_feature)
  29.         out = out[-1, :, :]
  30.         out = self.classifier(out)
  31.         return out
  33. net = rnn_classify()
  34. criterion = nn.CrossEntropyLoss()
  35. optimzier = torch.optim.Adadelta(net.parameters(), 1e-1)
  37. def get_acc(output, label):
  38.     total = output.shape[0]
  39.     _, pred_label = output.max(1)
  40.     num_correct = (pred_label == label).sum().data
  41.     # print(num_correct, total)
  42.     return num_correct
  44. def train(net, train_data, valid_data, num_epochs, optimizer, criterion):
  45.     if torch.cuda.is_available():
  46.         net = net.cuda()
  47.     for i in range(num_epochs):
  48.         train_loss = 0
  49.         train_acc = 0
  50.         net = net.train()
  51.         for im, label in train_data:
  52.             if torch.cuda.is_available():
  53.                 im = Variable(im.cuda())
  54.                 label = Variable(label.cuda())
  55.             else:
  56.                 im = Variable(im)
  57.                 label = Variable(label)
  58.             # forward
  59.             output = net(im)
  60.             total = output.shape[0]
  61.             loss = criterion(output, label)
  62.             # backward
  63.             optimizer.zero_grad()
  64.             loss.backward()
  65.             optimizer.step()
  67.             train_loss += loss.data.cpu().numpy()/float(total)
  68.             train_acc += get_acc(output, label).cpu().numpy()/float(total)
  69.         if valid_data is not None:
  70.             valid_loss = 0
  71.             valid_acc = 0
  72.             net = net.eval()
  73.             for im, label in valid_data:
  74.                 if torch.cuda.is_available():
  75.                     im = Variable(im.cuda(), volatile=True)
  76.                     label = Variable(label.cuda(), volatile=True)
  77.                 else:
  78.                     im = Variable(im, volatile=True)
  79.                     label = Variable(label, volatile=True)
  80.                 output = net(im)
  81.                 total = output.shape[0]
  82.                 loss = criterion(output, label)
  83.                 valid_loss += loss.data.cpu().numpy()/float(total)
  84.                 valid_acc += get_acc(output, label).cpu().numpy()/float(total)
  85.             print("epoch: %d, train_loss: %f, train_acc: %f, valid_loss: %f, valid_acc:%f"
  86.                   % (i, train_loss/len(train_data),  train_acc/len(train_data),
  87.                   valid_loss/len(valid_data),  valid_acc/len(valid_data)))
  89.         else:
  90.             print("epoch= ", i, "train_loss= ", train_loss/len(train_data), "train_acc= ", train_acc/len(train_data))
  91. # 开始训练
  92. train(net, train_data, test_data, 10, optimzier, criterion)

上面定义的网络主要由LSTM网络和线性网络构成，LSTM网络接受图片序列，线性网络将它输出成最后的概率向量。在forward时要注意一个细节，out=out[-1, :, ]，这是因为循环神经网络的输出也是一个序列，这一行代码是在取输出序列的最后一个，应用在线性层作为最后的输出结果。

训练结果如下：

  1. epoch: 0, train_loss: 0.030151, train_acc: 0.286397, valid_loss: 0.016825, valid_acc:0.637739
  2. epoch: 1, train_loss: 0.009260, train_acc: 0.816498, valid_loss: 0.005889, valid_acc:0.892118
  3. epoch: 2, train_loss: 0.004151, train_acc: 0.921159, valid_loss: 0.003530, valid_acc:0.929936
  4. epoch: 3, train_loss: 0.002708, train_acc: 0.948711, valid_loss: 0.002165, valid_acc:0.958798
  5. epoch: 4, train_loss: 0.002029, train_acc: 0.961521, valid_loss: 0.002024, valid_acc:0.961286
  6. epoch: 5, train_loss: 0.001669, train_acc: 0.968533, valid_loss: 0.001499, valid_acc:0.972432
  7. epoch: 6, train_loss: 0.001411, train_acc: 0.973048, valid_loss: 0.001406, valid_acc:0.972731
  8. epoch: 7, train_loss: 0.001237, train_acc: 0.976679, valid_loss: 0.001217, valid_acc:0.977906
  9. epoch: 8, train_loss: 0.001122, train_acc: 0.978945, valid_loss: 0.001707, valid_acc:0.967456
  10. epoch: 9, train_loss: 0.000983, train_acc: 0.980960, valid_loss: 0.001669, valid_acc:0.967456

虽然仅仅通过10次迭代循环神经网络就取得了不错的精度，但是循环神经网络还是不适合处理图片类型的数据：

  • 第一个原因是图片并没有很强的序列关系，图片中的信息可以从左往右看，也可以从右往左看，甚至可以跳着随机看，不管是什么样的方式都能完整地理解图片信息；
  • 第二个原因是循环神经网络传递时，必须前面一个数据计算结束才能进行后面一个数据的计算，这对于大图片来说是非常慢的，但是卷积神经网络并不需要这样，因为它能够并行，在每一个卷积中，并不需要等待第一个卷积做完才能做第二个卷积，整体是可以同时进行的。

所以循环神经网络真正适用的场景应该是——序列预测。

2.3 词嵌入

再来介绍一个自然语言处理中的概念——词嵌入（word embedding），也可以称为词向量。

图像分类问题会使用one-hot编码，比如一共有5个类，那么第二类的编码就是 (0, 1, 0, 0, 0)，对于分类问题，这样当然特别简明。但是在自然语言处理中，因为单词的数目过多，这样做会导致输入维度过高，比如有10000个不同的词，那么用one-hot这样的方式定义效率就会非常低，每个单词都是10000维度的向量，其中只有一位是1，其余都是0，特别占用内存。除此之外，也不能体现单词的词性，因为每个单词都是one-hot，虽然有些单词在语义上会更加接近，但是one-hot没办法体现这个特点，所以必须使用另外一种方式定义每一个单词，这就引入了词嵌入。

词嵌入到底是什么意思呢？其实很简单，对于每个词，可以使用一个高维向量表示它，这里的高维向量和one-hot的区别在于，这个向量不再是0和1的形式，向量的每一位都是一些实数，而这些实数隐含着这个单词的某种属性。这样解释可能不太直接，先举四个例子，下面有四段话：
(1) The cat likes playing ball.
(2) The kitty likes playing wool.
(3) The dog likes playing ball.
(4) The boy likes playing ball.

重点分析里面的4个词，cat、kitty、dog和boy。如果使用one-hot，那么cat就可以表示成 (1, 0, 0, 0)，kitty就可以表示成 (0, 1, 0, 0)，但是cat和kitty其实都表示小猫，所以这两个词语义是接近的，但是one-hot并不能体现这个特点。

下面使用词嵌入的方式来表示这4个词，假如使用一个二维向量 (a, b)来表示一个词，其中 a, b 分别代表这个词的一种属性，比如 a代表是否喜欢玩球，b代表是否喜欢玩毛线，并且这个数值越大表示越喜欢，这样就能够定义每一个词的词嵌入，并且通过这个来区分语义，下面来解释下原因。

对于cat，可以定义它的词嵌入是 (-1, 4)，因为它不喜欢玩球，喜欢玩毛线；而对于kitty，它的词嵌入可以定义为 (-2, 5)；那么对于dog，它的词嵌入就是 (3, -2)，因为它喜欢玩球，不喜欢玩毛线；最后对于boy，它的词向量就是 (-2, -3)，因为这两样东西它都不喜欢。定义好了这样的词嵌入，怎么去定义它们之间的语义相似度呢？可以通过词向量之间的夹角来定义它们的相似度。

通过上面的例子我们能够看出来词嵌入对于单词的表示具有很好的优势，但是问题来了，对于一个词，怎么知道如何去定义它的词嵌入？如果向量的维度只有5维，可能还能定义出来，如果向量的维数是100维，那么怎么知道每一维体式多少呢？这个问题自然是交给神经网络去解决，只需要定义我们想要的维度，比如100维，神经网络就会自己去更新每个词嵌入中的元素。而之前介绍过词嵌入的每个元素表示一种属性，当然对于维数比较低的时候，可能我们能够推断出每一维具体的含义，然而维度比较高之后，我们并不需要关心每一维到底代表着什么含义，因为每一维都是网络自己学习到的属性，只需要知道词向量之间的夹角越小，表示它们之间的语义更加接近就可以了。这就好比卷积神经网络会对一张图片提取出很厚的特征图，并不需要关心网络提取到的特征到底是什么，只需要知道抽象的特征能够帮助我们正确分类图像。

2.3.1 词嵌入的PyTorch实现

PyTorch中的词嵌入是通过函数 nn.Embedding(m, n)来实现，其中m表示所有的单词数目，n表示词嵌入的维度，下面举一个例子：

  1. word_to_idx = { 'hello': 0, 'world': 1}
  2. embeds = nn.Embedding(2, 5)
  3. hello_idx = torch.LongTensor([word_to_idx['hello']])
  4. hello_idx = Variable(hello_idx)
  5. hello_embed = embeds(hello_idx)
  6. print(hello_embed)

运行结果：

  1. tensor([[-0.7987,  1.5127,  2.0559,  0.3684, -2.1065]],
  2.        grad_fn=<EmbeddingBackward>)

上面就是对输出的hello的词嵌入，下面来解释下代码。首先需要给每个单词建立一个一个对应下标，这样每个单词都可以用一个数字去表示。比如需要hello的时候，就可以用0表示。接着是词嵌入的定义 nn.Embedding(2, 5)，如上面介绍过的，表示有两个词，每个词向量是5维，也就是一个 2 × 5 2\times52×5的矩阵，只不过矩阵里面的每个元素是可以被学习更新的，所以如果有1000个词，每个词向量希望是100维，就可以这样定义词嵌入 nn.Embedding(1000, 100)。访问每一个词的词向量需要将Tensor转换成Variable，因为词向量也是网络中更新的参数，所以在计算图中需要通过Variable访问。另外这里的词向量只是初始的词向量，并没有经过学习更新，需要建立神经网络优化更新，修改词向量里面的参数使得词向量能够表示不同的词，且语义相近的词能够有更小的夹角。

参考文献：

https://www.jianshu.com/p/298116084ec7
https://zybuluo.com/hanbingtao/note/541458
深度学习入门之PyTorch

发表评论

表情：
评论列表 （有 0 条评论，453人围观）

还没有评论，来说两句吧...

相关阅读

    相关 循环神经网络（RNN）

    对于人类而言，以前见过的事物会在脑海中留下记忆，虽然随后记忆会慢慢消失，但是每当经过提醒，人们往往可以重拾记忆。在神经网络中也是一样，之前介绍的CNN模型都是与时间序列无关的模

    古城微笑少年丶古城微笑少年丶/ 0 赞/ 454 阅读