图解算法：八大排序算法

r囧r小猫 2022-11-07 14:51 125阅读 0赞

### 目录 ###

*  第一章 性能分析
 *   *  1.1、时间复杂度
     *  1.2、空间复杂度
     *  1.3、排序算法分类
     *  1.4、排序算法比较
 *  第二章 冒泡排序
 *   *  2.1、算法介绍
     *  2.2、算法演示
     *  2.3、算法实现
 *  第三章 选择排序
 *   *  3.1、算法介绍
     *  3.2、算法演示
     *  3.3、算法实现
 *  第四章 插入排序
 *   *  4.1、算法介绍
     *  4.2、算法演示
     *  4.3、算法实现
 *  第五章 希尔排序
 *   *  5.1、算法介绍
     *  5.2、算法演示
     *  5.3、算法实现
 *  第六章 快速排序
 *   *  6.1、算法介绍
     *  6.2、算法演示
     *  6.3、算法实现
 *  第七章 归并排序
 *   *  7.1、算法介绍
     *  7.2、算法演示
     *  7.3、算法实现
 *  第八章 基数排序
 *   *  8.1、算法介绍
     *  8.2、算法演示
     *  8.3、算法实现
 *  第九章 堆排序
 *   *  9.1、算法介绍
     *  9.2、算法演示
     *  9.3、算法实现

--------------------

> 项目地址：https://gitee.com/caochenlei/algorithms

# 第一章 性能分析 #

## 1.1、时间复杂度 ##

**时间频度：**

一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，他花费时间就多，一个算法中的语句执行次数称为语句频度或时间频度，记为 T(n)。

**遵循规则：**

*  随着输入规模的增大，算法中常数操作可以忽略不计，例如：T(n)=2n2\+3n+20中的常数20可以忽略不计。
 *  随着输入规模的增大，除最高次项外其他次项可忽略，例如：T(n)=2n2\+3n+20中的低次项3n可以忽略不计。
 *  随着输入规模的增大，最高次项相乘的常数可以忽略，例如：T(n)=2n2\+3n+20中的系数2可以忽略不计。

**啥是时间复杂度：**

一般情况下，算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数，用 T(n) 表示，若有某个辅助函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数，记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。T(n) 不同，但时间复杂度可能相同。 例如：T(n)=n²+7n+6 与 T(n)=3n²+2n+2 中的 T(n) 不同，但时间复杂度相同，都为 O(n²)。

**常见时间复杂度：**

*  常数阶：O(1)
 *  对数阶：O(log2n)
 *  线性阶：O(n)
 *  线性对数阶：O(nlog2n)
 *  平方阶：O(n2)
 *  立方阶：O(n3)
 *  k 次方阶：O(nk)
 *  指数阶 O(2n)

时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜ Ο(nk) ＜Ο(2n) 。

**平均时间复杂度：**

平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。

**最坏时间复杂度：**

最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长。

## 1.2、空间复杂度 ##

类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，他也是问题规模 n 的函数。

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模 n 有关，他随着 n 的增大而增大，当 n 较大时，将占用较多的存储单元，例如快速排序和归并排序算法、基数排序就属于这种情况。在做算法分析时，主要讨论的是时间复杂度。从用户使用体验上看，更看重的程序执行的速度，一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间。

## 1.3、排序算法分类 ##

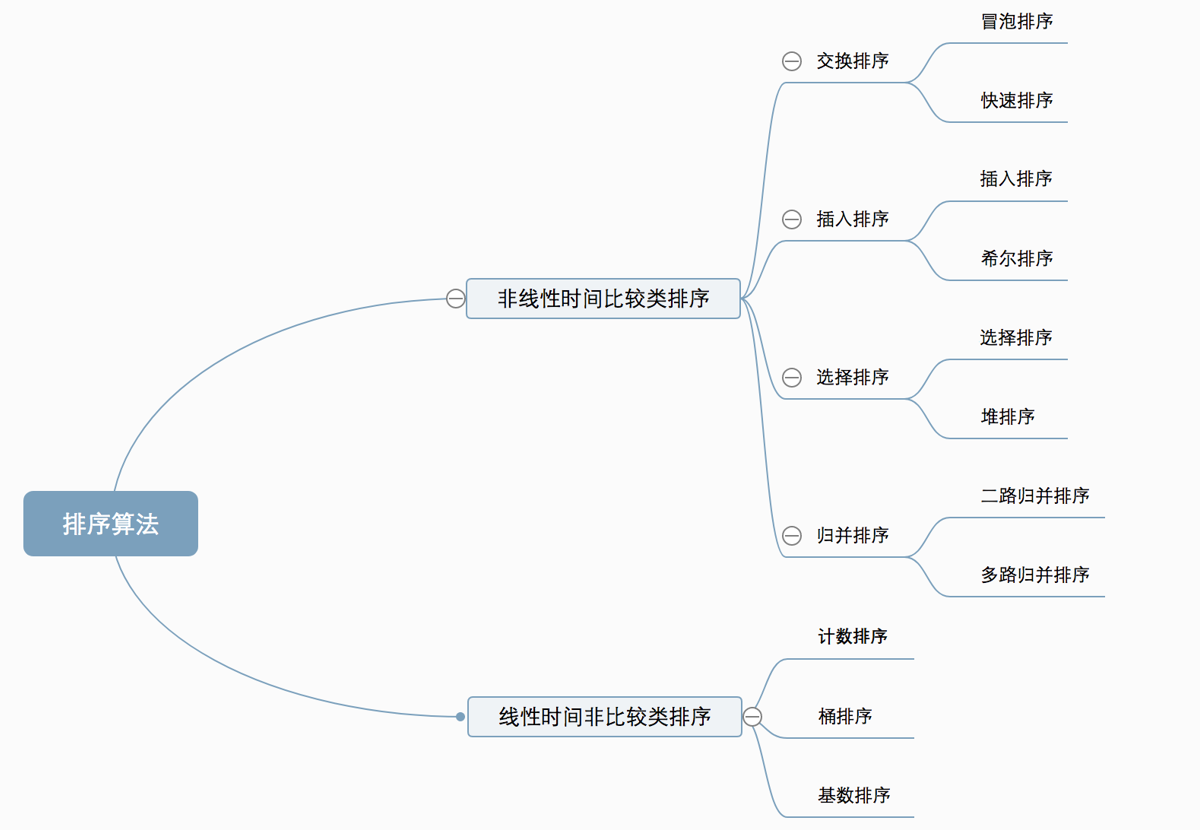
![08fddba9e02ef28dc99ced4b2a27b76b.png][]

## 1.4、排序算法比较 ##

算法比较：

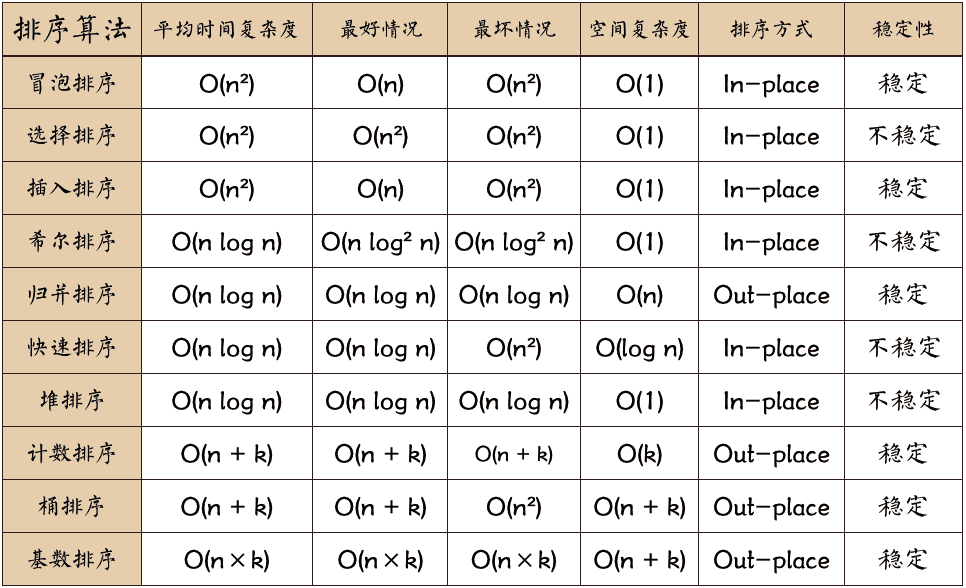
![c2d5d3fc7cfdf69628e7c73ef52b83a5.png][]

相关术语：

*  n：数据规模
 *  k：桶的个数
 *  In-place：不占用额外内存
 *  Out-place：占用额外内存
 *  稳定：如果 a 原本在 b 前面，并且 a=b，排序之后 a 仍然在 b 的前面
 *  不稳定：如果 a 原本在 b 的前面，并且 a=b，排序之后 a 可能会出现在 b 的后面

# 第二章 冒泡排序 #

## 2.1、算法介绍 ##

冒泡排序（Bubble Sort）是一种比较简单的排序算法。他的核心思想是：比较相邻的元素，如果第一个比第二个大，就交换他们两个。对每一对相邻元素做同样的工作，从开始的第一对到结尾的最后一对，这步做完后，最后的元素应该会是最大的数。每次过后，需要排序的元素就越来越少，对剩下需要排序的元素重复上面的步骤，直到没有任何一对数字需要比较。

## 2.2、算法演示 ##

![c18286f4397a581d06053b9040fbd16f.gif][]

## 2.3、算法实现 ##

public static void bubbleSort(int[] arr) { 
        for (int i = 0; i < arr.length; i++) { 
            for (int j = 0; j < arr.length - 1 - i; j++) { 
                if (arr[j] > arr[j + 1]) { 
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

# 第三章 选择排序 #

## 3.1、算法介绍 ##

选择排序（Selection Sort）是一种简单直观的排序算法。他的核心思想是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（或最大）的一个元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。

## 3.2、算法演示 ##

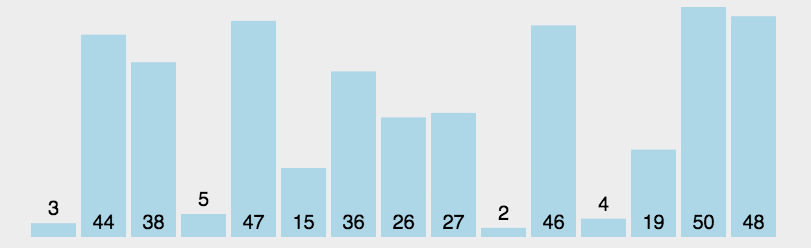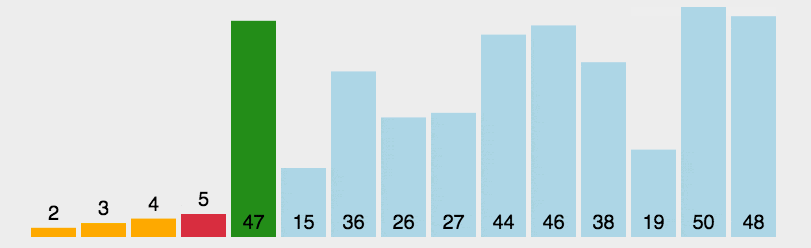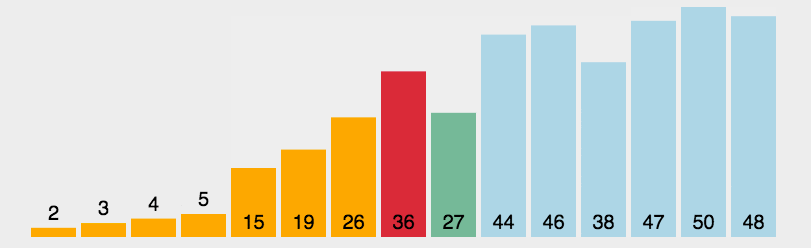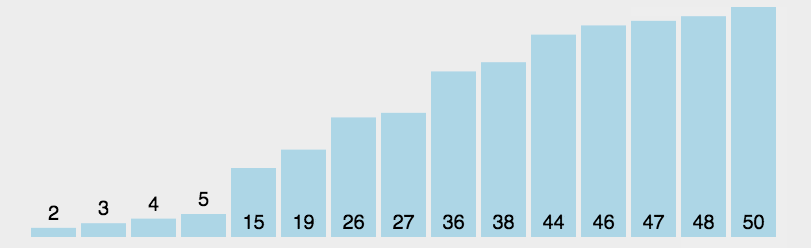
![ffcc8cb60fd6bbeadff7450b6d2edab9.gif][]

## 3.3、算法实现 ##

public static void selectionSort(int[] arr) { 
        for (int i = 0; i < arr.length - 1; i++) { 
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) { 
                if (arr[j] < arr[minIndex]) { 
                    minIndex = j;
                }
            }
            if (minIndex != i) { 
                int temp = arr[minIndex];
                arr[minIndex] = arr[i];
                arr[i] = temp;
            }
        }
    }

# 第四章 插入排序 #

## 4.1、算法介绍 ##

插入排序（Insertion Sort）一般也被称为直接插入排序。他的核心思想是：将一个待排序的数组分成两部分，前一部分代表是有序序列，后一部分代表未排序序列，刚开始之时，将第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面，直到未排序序列全部扫描完毕为止。

## 4.2、算法演示 ##

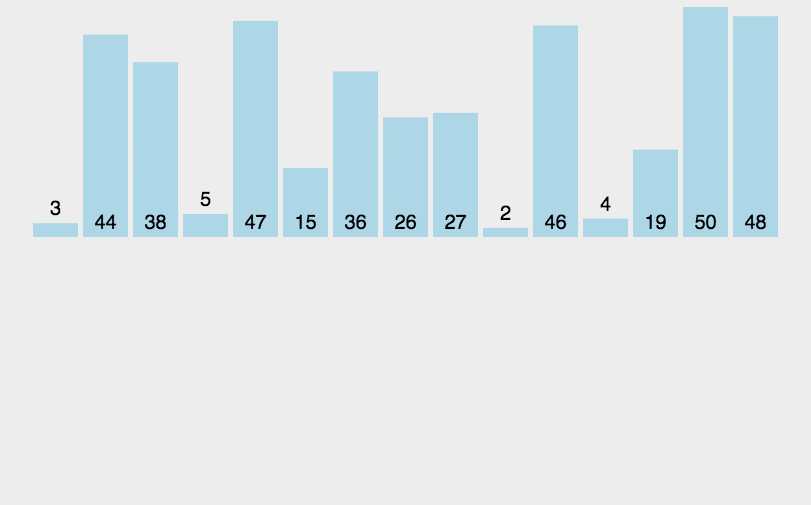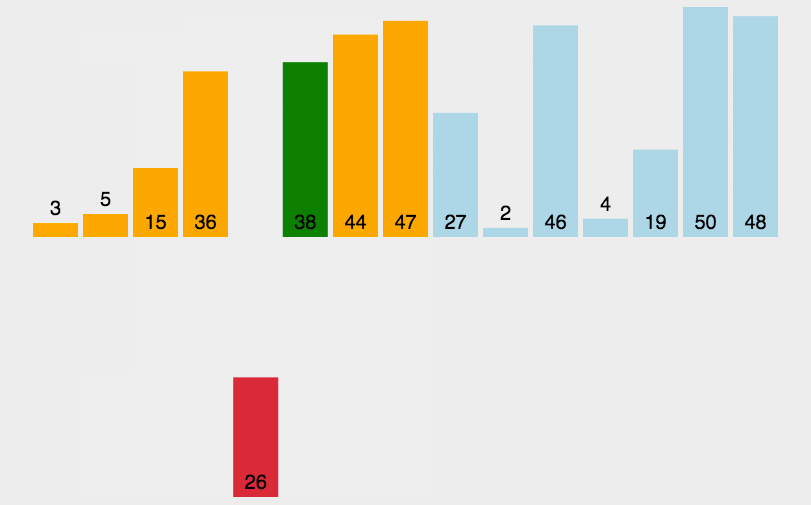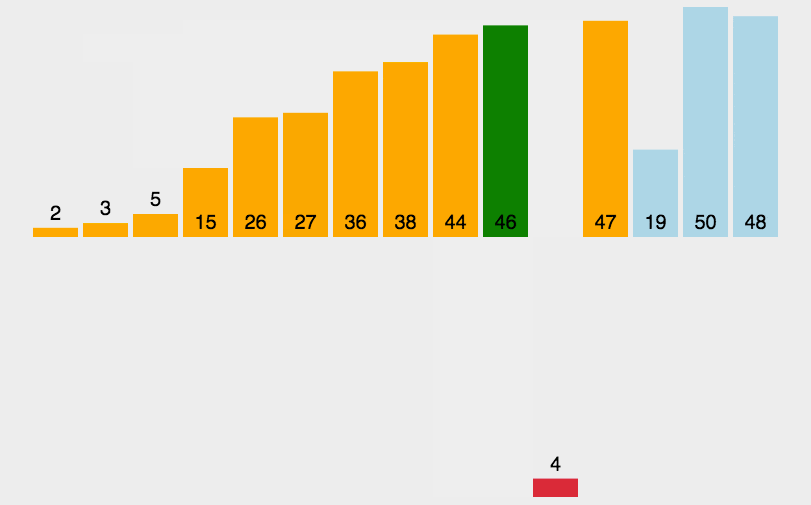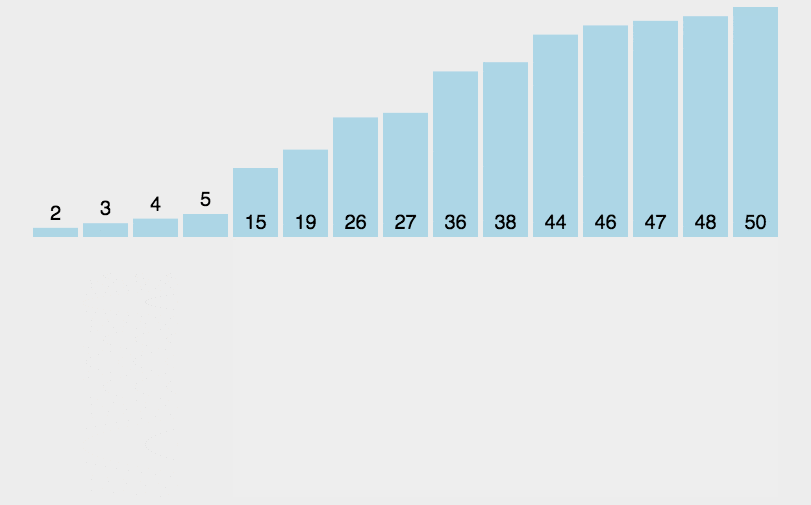
![45b6ffe08e63671925e04aa6c1d53399.gif][]

## 4.3、算法实现 ##

public static void insertionSort(int[] arr) { 
        for (int i = 1; i < arr.length; i++) { 
            for (int j = i - 1; j >= 0; j -= 1) { 
                if (arr[j] > arr[j + 1]) { 
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

# 第五章 希尔排序 #

## 5.1、算法介绍 ##

希尔排序（Shell Sort）一般也被称为缩小增量排序，希尔排序是对插入排序的一种改进。他的核心思想是：按下标的一定增量进行分组，对每组使用插入排序算法排序，随着增量逐渐减少，每组包含的元素越来越多，当增量减至 1 时，恰被分成一组，算法便终止。

## 5.2、算法演示 ##

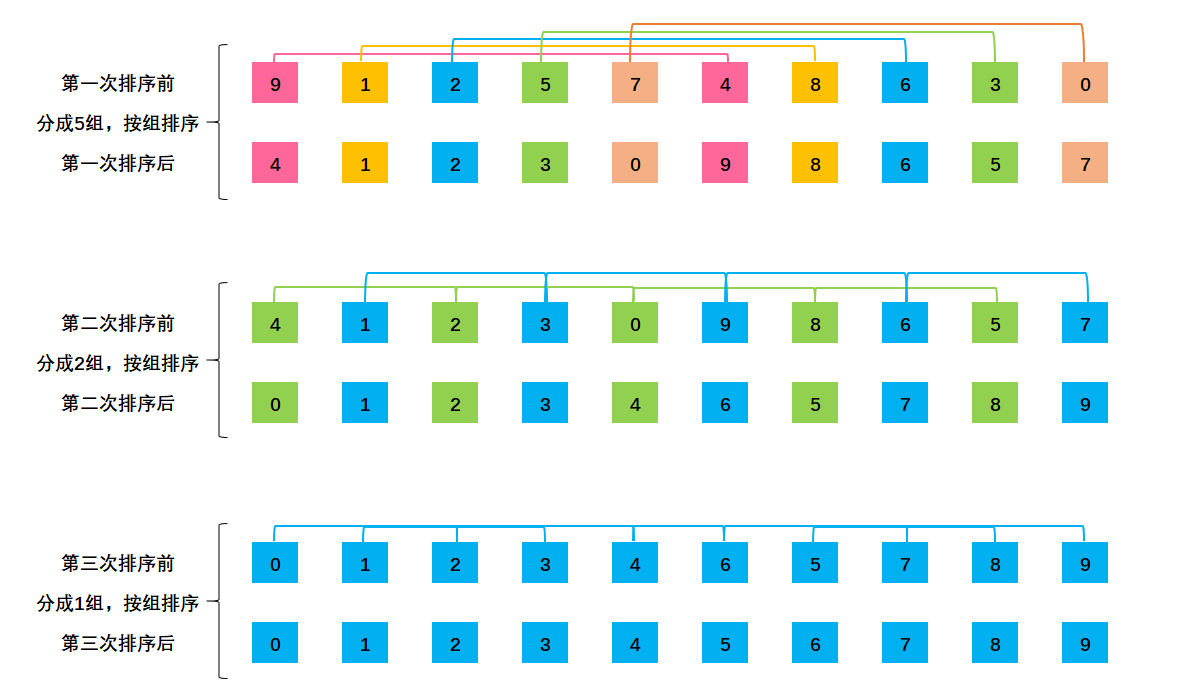
![601985591f2abe9fe3a963f33fd66cc4.png][]

## 5.3、算法实现 ##

public static void shellSort(int[] arr) { 
        for (int step = arr.length / 2; step > 0; step /= 2) { 
            //核心代码就是插入排序，把所有的一替换成step
            for (int i = step; i < arr.length; i++) { 
                for (int j = i - step; j >= 0; j -= step) { 
                    if (arr[j] > arr[j + step]) { 
                        int temp = arr[j];
                        arr[j] = arr[j + step];
                        arr[j + step] = temp;
                    }
                }
            }
        }
    }

# 第六章 快速排序 #

## 6.1、算法介绍 ##

快速排序（Quick Sort）是对冒泡排序算法的一种改进。他的核心思想是：首先设定一个基准值，通过该基准值将数组分成左右两部分，将小于或等于基准值的数据放到数组的左边，将大于或等于基准值的数据放到数组的右边。此时左边部分中各元素都小于或等于基准值，而右边部分中各元素都大于或等于基准值。然后左边和右边的数据又可以分别独立排序。对于左侧的数组数据，又可以再取一个基准值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值，右侧的数组数据也可以做类似处理。重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了。

## 6.2、算法演示 ##

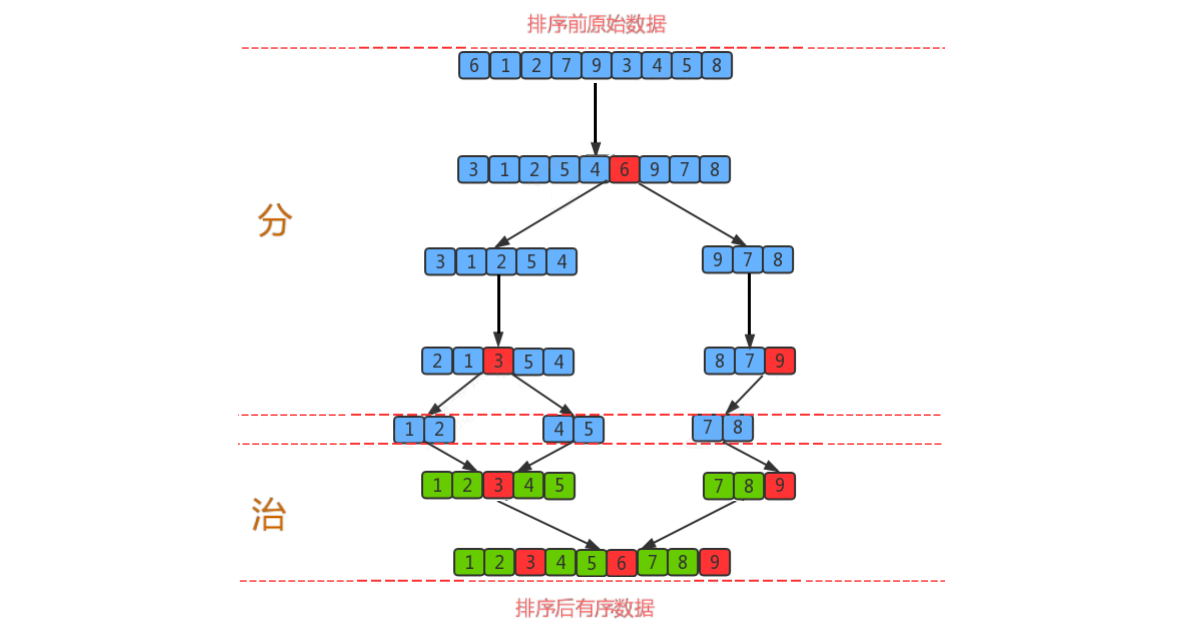
![2fea0a820b6a69ef25feed232ea82d38.png][]

## 6.3、算法实现 ##

public static void quickSort(int[] arr) { 
        quickSort(arr, 0, arr.length - 1);
    }
    
    public static void quickSort(int[] arr, int left, int right) { 
        int l = left;                       //左下标
        int r = right;                      //右下标
        int p = arr[(left + right) / 2];    //基准值
        //交换基准值左右大小值
        while (l < r) { 
            //在基准值的左边一直找，直到找到大于等于基准值后才退出
            while (arr[l] < p) {  l++; }
            //在基准值的右边一直找，直到找到小于等于基准值后才退出
            while (arr[r] > p) {  r--; }
            //如果l>=r则说明：基准值左侧的值都小于基准值右侧的值
            if (l >= r) { 
                break;
            }
            //将基准值左侧找到的小值与基准值右侧找到的大值进行交换
            int temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;
            //如果交换完后，发现这个arr[r]等于基准值，l++向前移
            if (arr[r] == p) {  l++; }
            //如果交换完后，发现这个arr[l]等于基准值，r--向前移
            if (arr[l] == p) {  r--; }
        }
        //这一步来防止堆栈溢出
        if (l == r) { 
            l++;
            r--;
        }
        //向左递归进行快速排序
        if (left < r) { 
            quickSort(arr, left, r);
        }
        //向右递归进行快速排序
        if (right > l) { 
            quickSort(arr, l, right);
        }
    }

# 第七章 归并排序 #

## 7.1、算法介绍 ##

归并排序（Merge Sort）是采用分治法的一个非常典型的应用。他的核心思想是：

1.  申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。
2.  设定两个指针，最初位置分别为两个已经排序序列的起始位置。
3.  比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。
4.  重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。

## 7.2、算法演示 ##

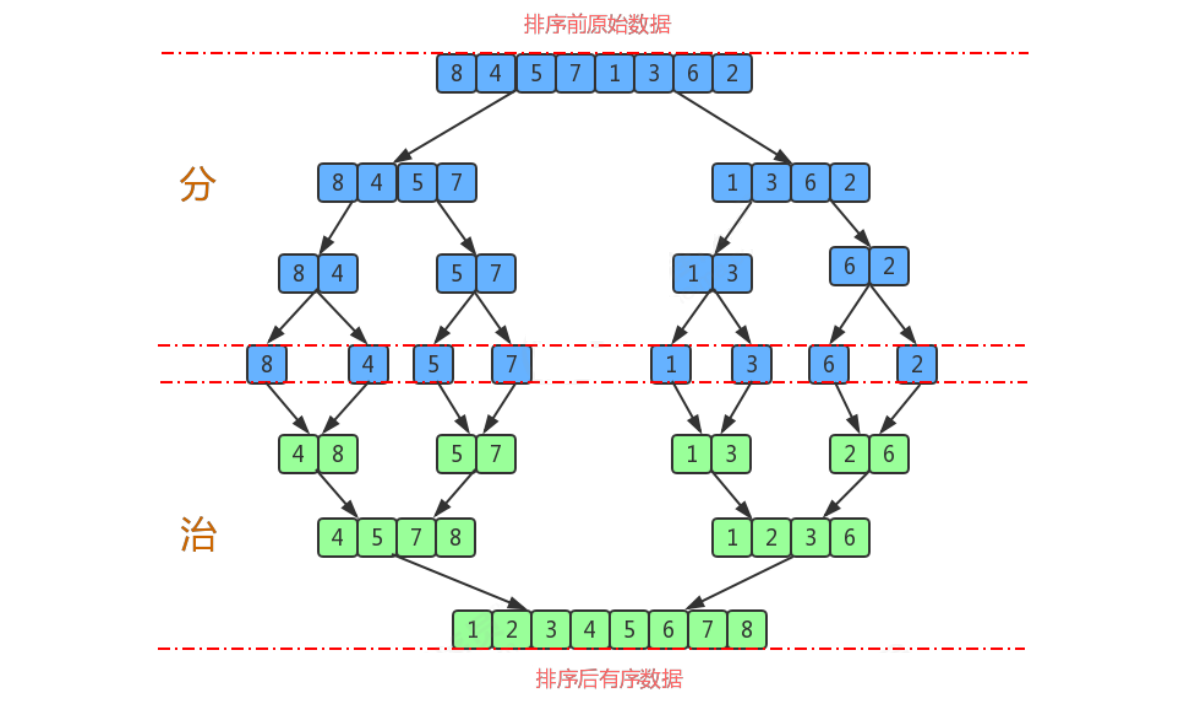
![c30ba54bc21c4c33d415e4f6f500690e.png][]

当分完以后，我们还需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将`[4,5,7,8]`和`[1,2,3,6]`两个已经有序的子序列，合并为最终序列`[1,2,3,4,5,6,7,8]`，来看下实现步骤，特别注意，以下步骤是`public static void merge(...)`方法的核心步骤。

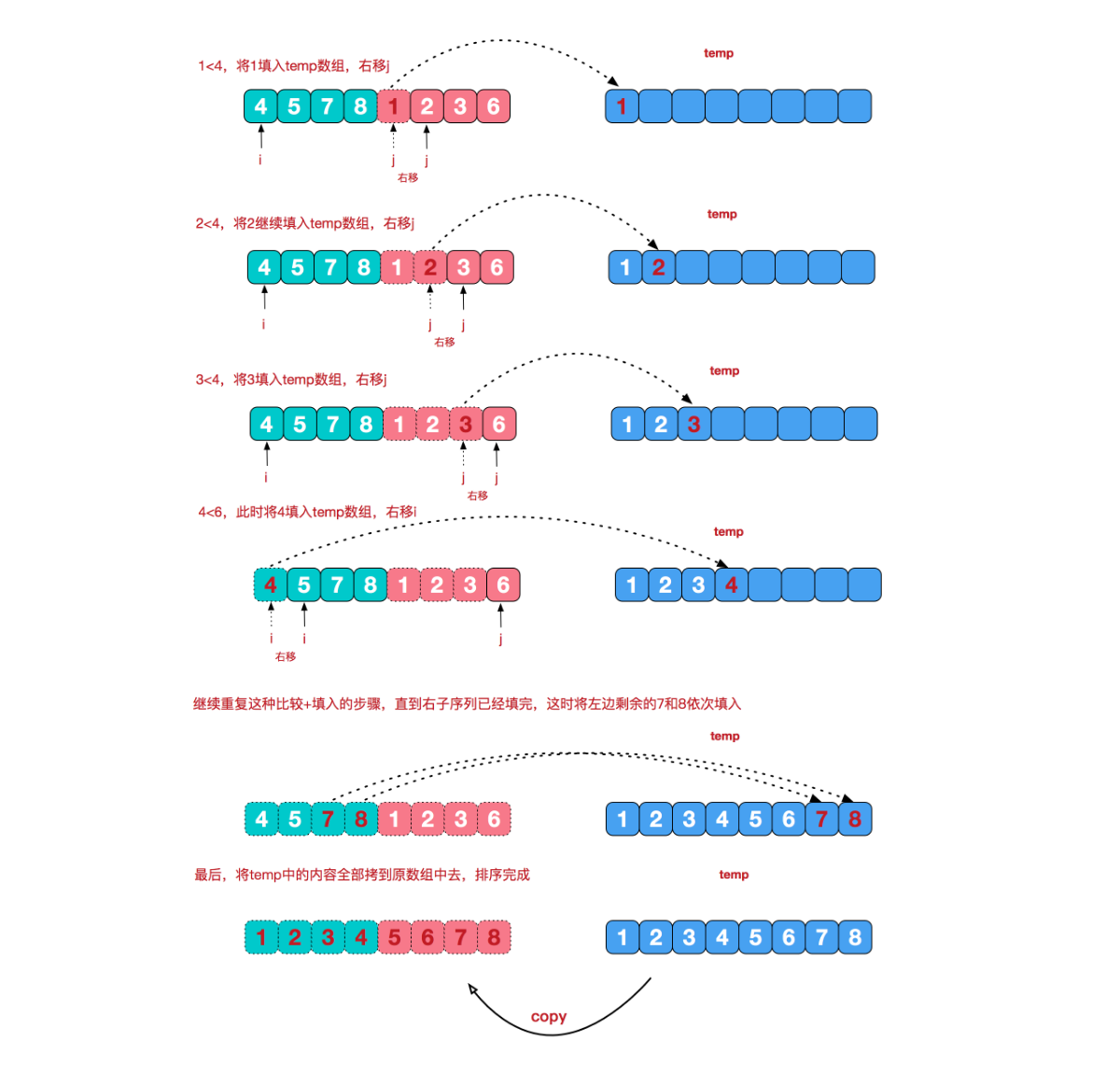
![3578c956c412a68d5566a4034e5405b8.png][]

## 7.3、算法实现 ##

public static void mergeSort(int[] arr) { 
        int temp[] = new int[arr.length];
        mergeSort(arr, 0, arr.length - 1, temp);
    }
    
    public static void mergeSort(int[] arr, int left, int right, int[] temp) { 
        if (left < right) { 
            int middle = (left + right) / 2;                //首先获取中间索引
            mergeSort(arr, left, middle, temp);             //向左递归进行分解
            mergeSort(arr, middle + 1, right, temp);    	//向右递归进行分解
            merge(arr, left, middle, right, temp);          //合并左右两个数组
        }
    }
    
    public static void merge(int[] arr, int left, int middle, int right, int[] temp) { 
        int pl = left;          //定义一个指针，指向左边有序序列的初始索引
        int pr = middle + 1;    //定义一个指针，指向右边有序序列的初始索引
        int i = left;           //定义一个指针，指向temp数组的初始化索引
        //比较左右两边序列中的元素大小，把小的数填充到 temp
        while (pl <= middle && pr <= right) { 
            if (arr[pl] <= arr[pr]) { 
                temp[i++] = arr[pl++];
            } else { 
                temp[i++] = arr[pr++];
            }
        }
        //左边的有序序列还有剩余的元素，就全部填充到 temp
        while (pl <= middle) { 
            temp[i++] = arr[pl++];
        }
        //右边的有序序列还有剩余的元素，就全部填充到 temp
        while (pr <= right) { 
            temp[i++] = arr[pr++];
        }
        //将 temp 数组中的元素拷贝到 arr 数组对应位置处
        for (int index = left; index <= right; index++) { 
            arr[index] = temp[index];
        }
    }

# 第八章 基数排序 #

## 8.1、算法介绍 ##

基数排序（Radix Sort）属于“分配式排序”（Distribution Sort），又称“桶子法”（Bucket Sort），基数排序是桶排序的扩展，他的核心思想是：将所有待比较的数值统一为同样的数位长度，数位较短的数前面补零。通过元素的各个位的值，将要排序的元素分配至某些桶中，然后按照桶的顺序，依次从低位桶顺序获取数据放回原数组中，重复上述的过程，这样从最低位排序一直到最高位排序完成以后，数组就变成一个有序序列。

## 8.2、算法演示 ##

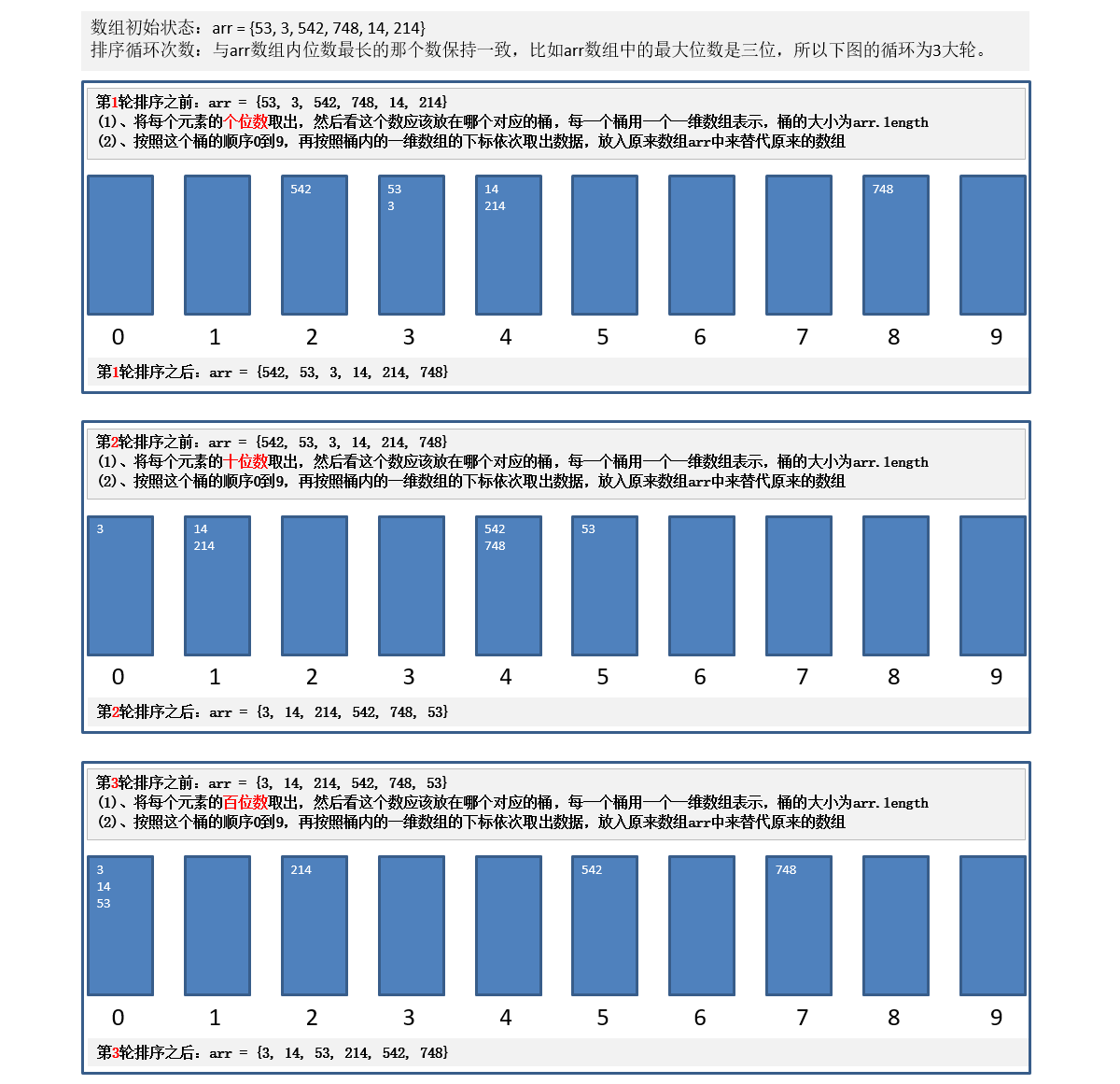
![e8261294ee3fec9fc9f49bea589f68c3.png][]

## 8.3、算法实现 ##

public static void radixSort(int[] arr) { 
        //获取当前数组中的最大值的位数
        int maxElementLength = String.valueOf(Arrays.stream(arr).max().getAsInt()).length();
        //创建十个桶，每个桶是一维数组
        int[][] bucket = new int[10][arr.length];
        //十个索引指向对应桶内元素位置
        int[] bucketIndex = new int[10];
        //开始循环将各位数放入桶中排序
        for (int i = 0, n = 1; i < maxElementLength; i++, n *= 10) { 
            for (int j = 0; j < arr.length; j++) {               //循环获取每一个元素值
                int digit = arr[j] / n % 10;                    //获取当前位数字（0-9）
                bucket[digit][bucketIndex[digit]] = arr[j];     //放入指定的桶内（0-9）
                bucketIndex[digit]++;                           //桶内的索引加加
            }
            int index = 0;                                      //用于指向原数组的索引，起始下标为零
            for (int k = 0; k < bucketIndex.length; k++) {       //依次获取桶内数据并重新填充到原数组
                if (bucketIndex[k] != 0) {                       //桶索引不等于零就说明这个桶内有数据
                    for (int l = 0; l < bucketIndex[k]; l++) {   //有数据就把这个桶内的数据一一拿出来
                        arr[index++] = bucket[k][l];            //拿出来以后就放到原数组中的指定位置
                    }
                }
                bucketIndex[k] = 0;                             //这个桶内数据拿完，需要让这个桶重置
            }
        }
    }

# 第九章 堆排序 #

## 9.1、算法介绍 ##

堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。他的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点，将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余`n-1`个元素重新构造成一个堆，这样会得到`n`个元素的次小值。如此反复执行，便能得到一个有序序列了。

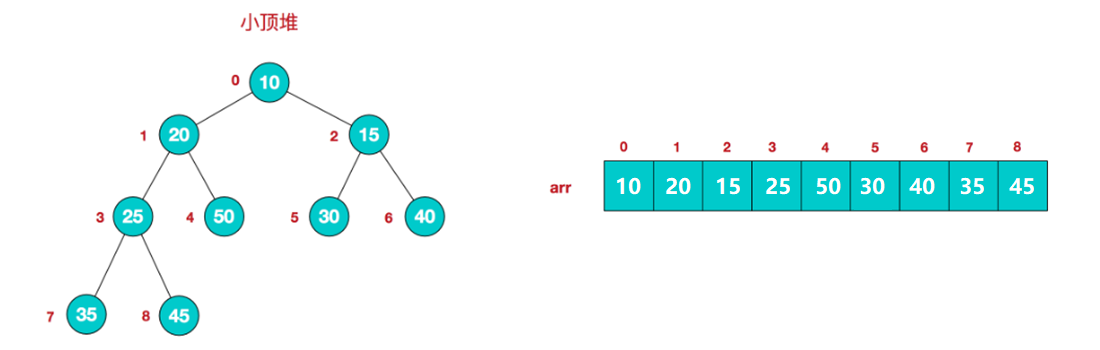
每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆，这里没有要求结点的左孩子的值和右孩子的值的大小关系。

大顶堆特点（i从0开始编号，对应第几个节点）：`arr[i] >= arr[2*i+1] && arr[i] >= arr[2*i+2]`，升序排序采用大顶堆。

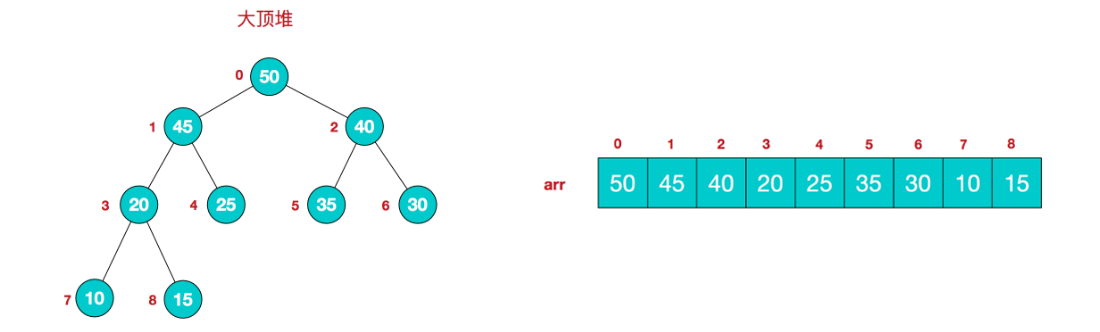
![cc7a36e9f3fbef56e31f68dc4c165de1.png][]

每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆，这里没有要求结点的左孩子的值和右孩子的值的大小关系。

大顶堆特点（i从0开始编号，对应第几个节点）：`arr[i] <= arr[2*i+1] && arr[i] <= arr[2*i+2]`，降序排序采用小顶堆。

![f3cfe6e3b381ad473260a576700d245d.png][]

## 9.2、算法演示 ##

**步骤一、将给定无序序列构造成一个大顶堆，一般升序采用大顶堆，降序采用小顶堆。**

（1）假设给定一个无序序列的结构如下：

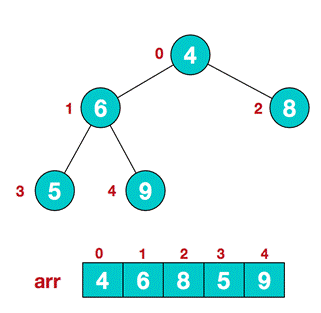
![e8025f54f178350b61d81dffc76c8b8e.gif][]

（2）我们从最后一个非叶子结点6开始，从左至右，从下至上进行调整。

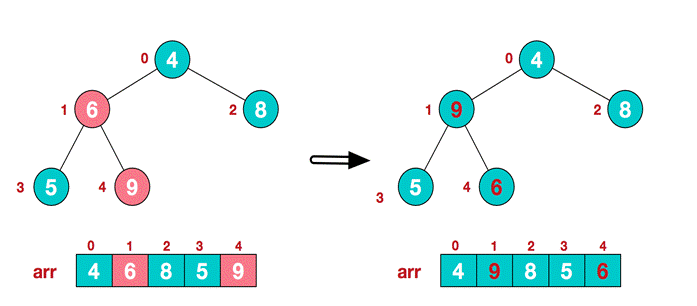
![36f0200025cf126c02dcf630917b80af.gif][]

（3）找到第二个非叶节点4，由于\[4,9,8\]中9元素最大，4和9交换。

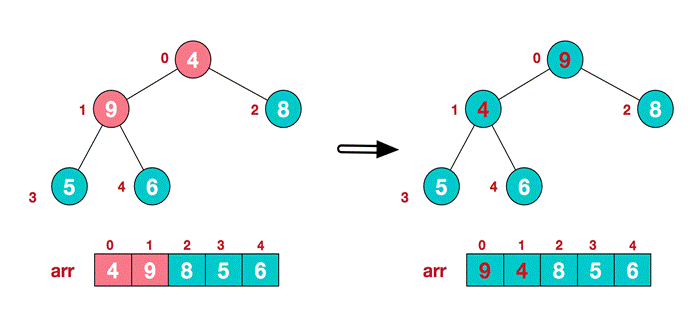
![b67ced8691a1501fc3277dd56ce9c6e6.gif][]

（4）这时交换导致了子根\[4,5,6\]结构混乱，继续调整，\[4,5,6\]中6最大，交换4和6。

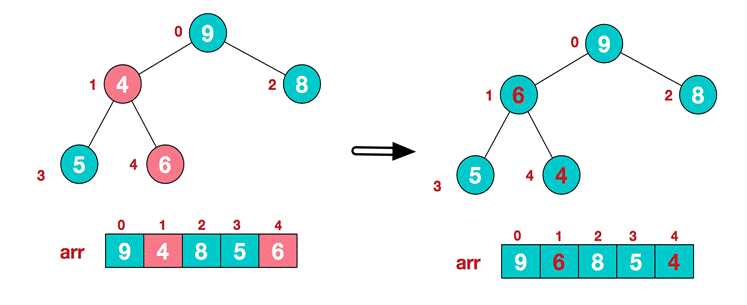
![da6d674a3957816e348be2cf596e0cf3.gif][]

此时，我们就将一个无序序列构造成了一个大顶堆。

**步骤二、将堆顶元素与末尾元素进行交换，使末尾元素最大，然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素，如此重复以上操作。**

（1）将堆顶元素9和末尾元素4进行交换。

![1651ae66f3b5a3732a84144027eb47fb.gif][]

（2）重新调整结构，使其继续满足堆定义。

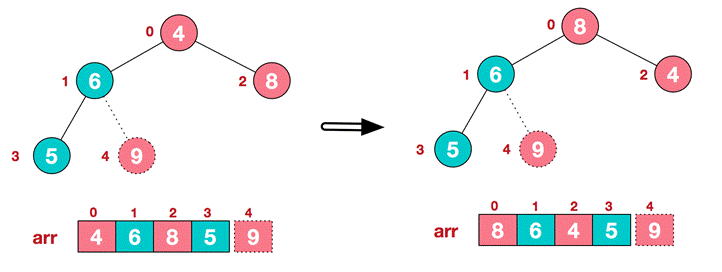
![6de9302b37823c463386fe0d89e6c9b3.gif][]

（3）再将堆顶元素8与末尾元素5进行交换，得到第二大元素8。

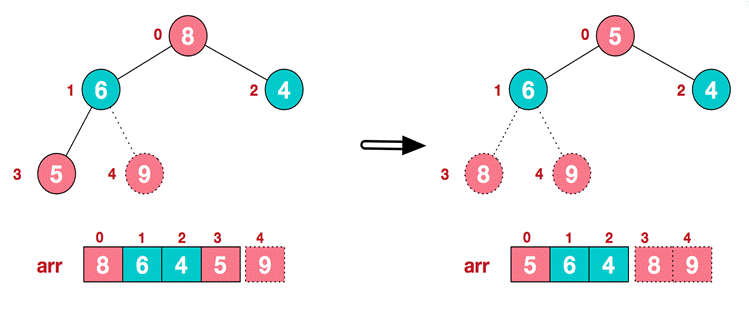
![45de30b1962aeee4b6956d296e6a9681.gif][]

（4）后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序。

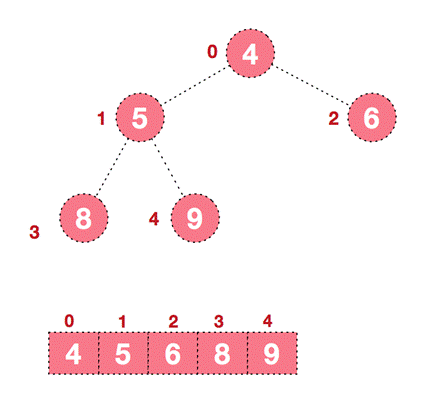
![49cb424aeeaaafbbe3a305320d3d4ebb.gif][]

## 9.3、算法实现 ##

//堆排序
    public static void heapSort(int arr[]) { 
        //创建大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) { 
            heapAdjust(arr, i, arr.length);
        }
        //调整大顶堆
        for (int i = arr.length - 1; i > 0; i--) { 
            //交换元素
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            //调整新堆
            heapAdjust(arr, 0, i);
        }
    }
    
    //堆调整
    public static void heapAdjust(int arr[], int index, int length) { 
        //缓存当前结点
        int temp = arr[index];
        //开始循环调整
        for (int i = index * 2 + 1; i < length; i = i * 2 + 1) { 
            //说明左子结点的值小于右子结点的值
            if (i + 1 < length && arr[i] < arr[i + 1]) { 
                i++;
            }
            //说明当前子结点的值大于父结点的值
            if (arr[i] > temp) { 
                arr[index] = arr[i];
                index = i;
            } else { 
                break;
            }
        }
        //放到调整位置
        arr[index] = temp;
    }

[08fddba9e02ef28dc99ced4b2a27b76b.png]: /images/20221023/5ec5ac0f7b664119913b6a80484243e2.png
[c2d5d3fc7cfdf69628e7c73ef52b83a5.png]: /images/20221023/699e06c9ebb4414a83ab4a4dee61b999.png
[c18286f4397a581d06053b9040fbd16f.gif]: /images/20221023/03d3c4bd7bf8434dabbaff830fd52395.png
[ffcc8cb60fd6bbeadff7450b6d2edab9.gif]: /images/20221023/f9b16288839c4f11ae87e9a53056dbe9.png
[45b6ffe08e63671925e04aa6c1d53399.gif]: /images/20221023/eebac6045440410dae1ca7943fe42f58.png
[601985591f2abe9fe3a963f33fd66cc4.png]: /images/20221023/e1c567e04548458a99e9ff5051dfaf2f.png
[2fea0a820b6a69ef25feed232ea82d38.png]: /images/20221023/228080ca94024696be3a2dc45a7e7e29.png
[c30ba54bc21c4c33d415e4f6f500690e.png]: /images/20221023/c210238845eb400aa7b007e8711a3c46.png
[3578c956c412a68d5566a4034e5405b8.png]: /images/20221023/339c0dba07344a24a8c935d25c55ae78.png
[e8261294ee3fec9fc9f49bea589f68c3.png]: /images/20221023/b6739c591e064779a8589cedebb6f809.png
[cc7a36e9f3fbef56e31f68dc4c165de1.png]: /images/20221023/08e78d02c7a04ac2a7339eedacb0f2b7.png
[f3cfe6e3b381ad473260a576700d245d.png]: /images/20221023/24104e81070842b5a31032d19eca3d30.png
[e8025f54f178350b61d81dffc76c8b8e.gif]: /images/20221023/ee288b473a004a6dbed62922babd86f9.png
[36f0200025cf126c02dcf630917b80af.gif]: /images/20221023/59de82fae1ba4016813188cec966322e.png
[b67ced8691a1501fc3277dd56ce9c6e6.gif]: /images/20221023/537147f0316141f28055a41cd68090bc.png
[da6d674a3957816e348be2cf596e0cf3.gif]: /images/20221023/cec6cd61370b40feb05790bd9ad82b6f.png
[1651ae66f3b5a3732a84144027eb47fb.gif]: /images/20221023/0cc8a516230447dcaed5d1295361ab76.png
[6de9302b37823c463386fe0d89e6c9b3.gif]: /images/20221023/a5f25939b2304e4b9c71d14202cfd183.png
[45de30b1962aeee4b6956d296e6a9681.gif]: /images/20221023/115dede1f886447f9be98570d563dbd6.png
[49cb424aeeaaafbbe3a305320d3d4ebb.gif]: /images/20221023/8aacec489efb48ff9453aef060febd87.png