LeetCode - Hard - 37. Sudoku Solver

朱雀 2022-11-15 11:18 190阅读 0赞

Topic

  • Backtracking

Description

https://leetcode.com/problems/sudoku-solver/

Write a program to solve a Sudoku puzzle by filling the empty cells.

A sudoku solution must satisfy all of the following rules:

  1. Each of the digits 1-9 must occur exactly once in each row.
  2. Each of the digits 1-9 must occur exactly once in each column.
  3. Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

The '.' character indicates empty cells.

Example 1:

  1. Input: board = 
  2. [["5","3",".",".","7",".",".",".","."],
  3. ["6",".",".","1","9","5",".",".","."],
  4. [".","9","8",".",".",".",".","6","."],
  5. ["8",".",".",".","6",".",".",".","3"],
  6. ["4",".",".","8",".","3",".",".","1"],
  7. ["7",".",".",".","2",".",".",".","6"],
  8. [".","6",".",".",".",".","2","8","."],
  9. [".",".",".","4","1","9",".",".","5"],
  10. [".",".",".",".","8",".",".","7","9"]]
  11. Output: 
  12. [["5","3","4","6","7","8","9","1","2"],
  13. ["6","7","2","1","9","5","3","4","8"],
  14. ["1","9","8","3","4","2","5","6","7"],
  15. ["8","5","9","7","6","1","4","2","3"],
  16. ["4","2","6","8","5","3","7","9","1"],
  17. ["7","1","3","9","2","4","8","5","6"],
  18. ["9","6","1","5","3","7","2","8","4"],
  19. ["2","8","7","4","1","9","6","3","5"],
  20. ["3","4","5","2","8","6","1","7","9"]]
  21. Explanation: The input board is shown above and the only valid solution is shown below:

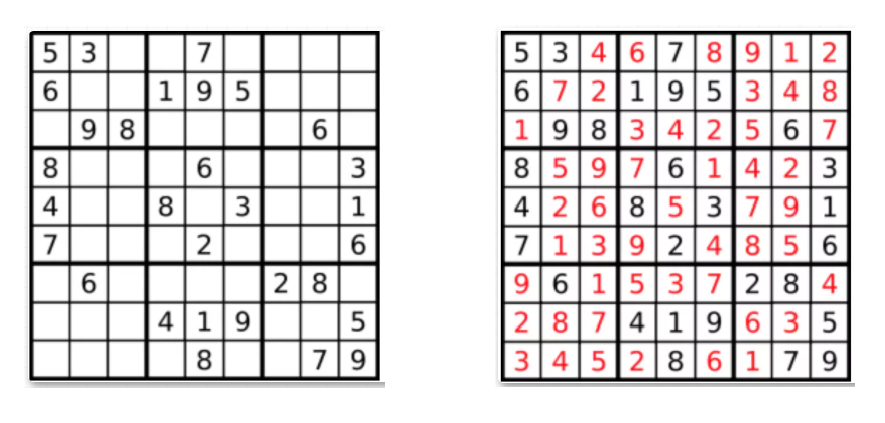
在这里插入图片描述

Constraints:

  • board.length == 9
  • board[i].length == 9
  • board[i][j] is a digit or '.'.
  • It is guaranteed that the input board has only one solution.

Analysis

思路分析

数独问题可以使用回溯法暴力搜索，用到二维递归，本题中数独每一个空格位置都要放一个数字，并检查数字是否合法。本题的树形图如下：

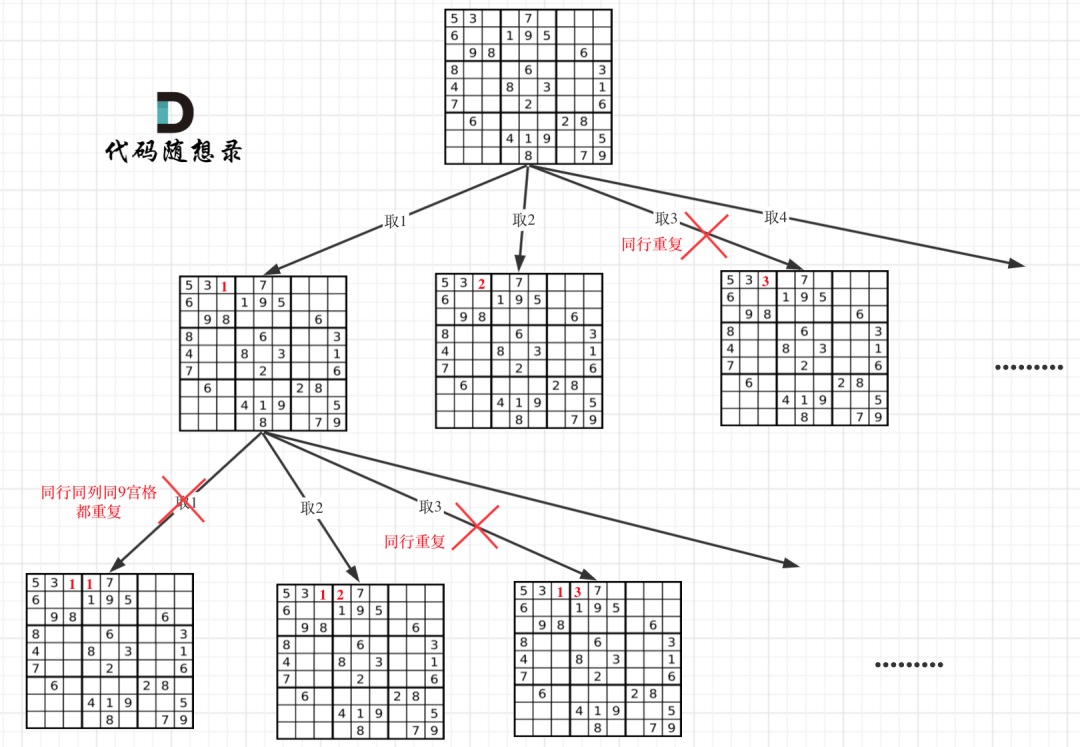
bc976e3ec6057ee059e8a93108c137e8.png

验证合法

判断数字放入数独终是否合法有如下三个维度：

  • 同行是否重复
  • 同列是否重复
  • 所属9宫格里是否重复

代码如下：

  1. private boolean isValid(char[][] board, int row, int col, int num) { 
  2.     // 所在行
  3.     for (int i = 0; i < 9; i++) { 
  4.         if (board[row][i] == num)
  5.             return false;
  6.     }
  8.     // 所在列
  9.     for (int i = 0; i < 9; i++) { 
  10.         if (board[i][col] == num)
  11.             return false;
  12.     }
  14.     // 所属9格
  15.     int startX = row / 3 * 3;
  16.     int startY = col / 3 * 3;
  18.     for (int i = startX; i < startX + 3; i++) { 
  19.         for (int j = startY; j < startY + 3; j++) { 
  20.             if (board[i][j] == num) { 
  21.                 return false;
  22.             }
  23.         }
  24.     }
  26.     return true;
  27. }

回溯三弄

函数签名

因为解数独找到一个符合的条件（就在树的叶子节点上）立刻就返回，相当于找从根节点到叶子节点一条唯一路径，所以需要使用boolean返回值。

代码如下：

  1. private boolean backtracking(char[][] board) { }

终止条件

本题递归不用终止条件，解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。

不用终止条件会不会死循环？递归的下一层的数独盘一定比上一层的数独盘多一个数，等数填满了数独盘自然就终止（填满当然好了，说明找到结果了），所以不需要终止条件。

遍历顺序

在思路分析树形图中可以看出我们需要的是一个二维递归（也就是两个for循环嵌套着递归）

一个for循环遍历数独盘的行，一个for循环遍历数独盘的列，一行一列确定下来之后，递归遍历这个位置放9个数字的可能性。

代码如下：

  1. private boolean backtracking(char[][] board) { 
  3.     for (int i = 0; i < 9; i++) { 
  4.         for (int j = 0; j < 9; j++) { 
  5.             if (board[i][j] != '.')
  6.                 continue;
  8.             for (char k = '1'; k <= '9'; k++) { 
  9.                 if (isValid(board, i, j, k)) { 
  10.                     board[i][j] = k;
  11.                     if (backtracking(board))//
  12.                         return true;
  13.                     board[i][j] = '.';
  14.                 }
  15.             }
  16.             return false;// 9个数都试完了，都不行，那么就返回false
  17.         }
  18.     }
  20.     return true;// 遍历完没有返回false，说明找到了合适数独盘位置了
  21. }

注意这里return false的地方，这里放return false 是有讲究的。

因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个数独盘找不到解决数独问题的解！

那么会直接返回， 这也就是为什么没有终止条件也不会永远填不满数独盘而无限递归下去！

降维打击

其实我们可以将二维数组降维至一维回溯的，代码如下：

  1. public void solveSudoku2(char[][] board) { 
  2.     backtracking2(board, 0, 0);
  3. }
  5. private boolean backtracking2(char[][] board, int i, int j) { 
  6.     if (i == 9)
  7.         return true;
  8.     if (j == 9)
  9.         return backtracking2(board, i + 1, 0);//换下一行遍历
  10.     if (board[i][j] != '.')
  11.         return backtracking2(board, i, j + 1);
  13.     for (char c = '1'; c <= '9'; c++) { //
  14.         if (isValid(board, i, j, c)) { 
  15.             board[i][j] = c;
  16.             if (backtracking2(board, i, j + 1))
  17.                 return true;
  18.             board[i][j] = '.';
  19.         }
  20.     }
  22.     return false;
  23. }

个人认为本”降维打击”方法更容易理解。

最终代码

移步至Submission。

参考资料

  1. Simple and Clean Solution / C++
  2. 回溯算法：解数独

Submission

  1. public class SudokuSolver { 
  3.     //方法一：回溯算法
  4.     public void solveSudoku(char[][] board) { 
  5.         backtracking(board);
  6.     }
  8.     private boolean backtracking(char[][] board) { 
  10.         for (int i = 0; i < 9; i++) { 
  11.             for (int j = 0; j < 9; j++) { 
  12.                 if (board[i][j] != '.')
  13.                     continue;
  15.                 for (char k = '1'; k <= '9'; k++) { 
  16.                     if (isValid(board, i, j, k)) { 
  17.                         board[i][j] = k;
  18.                         if (backtracking(board))//
  19.                             return true;
  20.                         board[i][j] = '.';
  21.                     }
  22.                 }
  23.                 return false;// 9个数都试完了，都不行，那么就返回false
  24.             }
  25.         }
  27.         return true;// 遍历完没有返回false，说明找到了合适数独盘位置了
  28.     }
  30.     //方法二：回溯算法2，不同与方法一的二维递归，本方法把二维降维到一维
  31.     //本人认为本方法更容易理解
  32.     public void solveSudoku2(char[][] board) { 
  33.         backtracking2(board, 0, 0);
  34.     }
  36.     private boolean backtracking2(char[][] board, int i, int j) { 
  37.         if (i == 9)
  38.             return true;
  39.         if (j == 9)
  40.             return backtracking2(board, i + 1, 0);
  41.         if (board[i][j] != '.')
  42.             return backtracking2(board, i, j + 1);
  44.         for (char c = '1'; c <= '9'; c++) { //
  45.             if (isValid(board, i, j, c)) { 
  46.                 board[i][j] = c;
  47.                 if (backtracking2(board, i, j + 1))
  48.                     return true;
  49.                 board[i][j] = '.';
  50.             }
  51.         }
  53.         return false;
  54.     }
  56.     private boolean isValid(char[][] board, int row, int col, int num) { 
  57.         // 所在行
  58.         for (int i = 0; i < 9; i++) { 
  59.             if (board[row][i] == num)
  60.                 return false;
  61.         }
  63.         // 所在列
  64.         for (int i = 0; i < 9; i++) { 
  65.             if (board[i][col] == num)
  66.                 return false;
  67.         }
  69.         // 所属9格
  70.         int startX = row / 3 * 3;
  71.         int startY = col / 3 * 3;
  73.         for (int i = startX; i < startX + 3; i++) { 
  74.             for (int j = startY; j < startY + 3; j++) { 
  75.                 if (board[i][j] == num) { 
  76.                     return false;
  77.                 }
  78.             }
  79.         }
  81.         return true;
  82.     }
  83. }

Test

  1. import static org.junit.Assert.*;
  3. import java.util.Arrays;
  5. import org.junit.Before;
  6. import org.junit.BeforeClass;
  7. import org.junit.Test;
  9. public class SudokuSolverTest { 
  11.     private char[][] array;
  13.     private static char[][] expected;
  15.     private static SudokuSolver obj;
  17.     @BeforeClass
  18.     public static void initOnce() { 
  19.         obj = new SudokuSolver();
  21.         expected = new char[][]{ { '5','3','4','6','7','8','9','1','2'},//
  22.                                 { '6','7','2','1','9','5','3','4','8'},//
  23.                                 { '1','9','8','3','4','2','5','6','7'},//
  24.                                 { '8','5','9','7','6','1','4','2','3'},//
  25.                                 { '4','2','6','8','5','3','7','9','1'},//
  26.                                 { '7','1','3','9','2','4','8','5','6'},//
  27.                                 { '9','6','1','5','3','7','2','8','4'},//
  28.                                 { '2','8','7','4','1','9','6','3','5'},//
  29.                                 { '3','4','5','2','8','6','1','7','9'}};
  30.     }
  32.     @Before
  33.     public void init() { 
  34.         array = new char[][]{ { '5','3','.','.','7','.','.','.','.'},//
  35.                             { '6','.','.','1','9','5','.','.','.'},//
  36.                             { '.','9','8','.','.','.','.','6','.'},//
  37.                             { '8','.','.','.','6','.','.','.','3'},//
  38.                             { '4','.','.','8','.','3','.','.','1'},//
  39.                             { '7','.','.','.','2','.','.','.','6'},//
  40.                             { '.','6','.','.','.','.','2','8','.'},//
  41.                             { '.','.','.','4','1','9','.','.','5'},//
  42.                             { '.','.','.','.','8','.','.','7','9'}};
  43.     }
  45.     @Test
  46.     public void test() {         
  47.         obj.solveSudoku(array);
  48.         //System.out.println(Arrays.deepToString(array));
  49.         for(int i = 0; i < expected.length; i++) { 
  50.             assertArrayEquals(expected[i], array[i]);
  51.         }
  52.     }
  54.     @Test
  55.     public void test2() {         
  56.         System.out.println(Arrays.deepToString(array));
  57.         obj.solveSudoku2(array);
  58. // System.out.println(Arrays.deepToString(array));
  59.         for(int i = 0; i < expected.length; i++) { 
  60.             assertArrayEquals(expected[i], array[i]);
  61.         }
  62.     }
  64. }

发表评论

表情：
评论列表 （有 0 条评论，190人围观）

还没有评论，来说两句吧...

相关阅读