279. 完全平方数
题目:
279. 完全平方数
题解:
1. 题解一:数学运算





2. 题解二:动态规划


n = 12先把 n 减去一个平方数,然后求剩下的数分解成平方数和所需的最小个数把 n 减去 1, 然后求出 11 分解成平方数和所需的最小个数,记做 n1那么当前方案总共需要 n1 + 1 个平方数把 n 减去 4, 然后求出 8 分解成平方数和所需的最小个数,记做 n2那么当前方案总共需要 n2 + 1 个平方数把 n 减去 9, 然后求出 3 分解成平方数和所需的最小个数,记做 n3那么当前方案总共需要 n3 + 1 个平方数下一个平方数是 16, 大于 12, 不能再分了。接下来我们只需要从 (n1 + 1), (n2 + 1), (n3 + 1) 三种方案中选择最小的个数,此时就是 12 分解成平方数和所需的最小个数了至于求 11、8、3 分解成最小平方数和所需的最小个数继续用上边的方法去求直到如果求 0 分解成最小平方数的和的个数, 返回 0 即可
代码:
1. 代码一:数学运算
import java.util.*;public class code279 {// 判断是否是[完全]平方数public static boolean isSquare(int n){int sqrt = (int) Math.sqrt(n);return sqrt * sqrt == n;}public static int numSquares(int n){// 判断答案是否是 1if(isSquare(n)){return 1;}// 判断答案是否是 4int temp = n;while(temp % 4 == 0){temp /= 4;}if(temp % 8 == 7){return 4;}// 判断答案是否是 2for(int i = 1; i * i <= n; i++){if(isSquare(n - i * i)){return 2;}}// 以上情况都排除的话,答案就是 3return 3;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);while(sc.hasNextInt()){int n = sc.nextInt();int res = numSquares(n);System.out.println(res);}}}
2. 代码二:动态规划
import java.util.*;public class code279 {// 方法2:动态规划public static int numSquares(int n) {// dp[i]表示 i 最少可以由几个[完全]平方数构成int dp[] = new int[n + 1]; // 默认初始化值都为0dp[0] = 0;for(int i = 1; i <= n; i++){dp[i] = i; // 最坏的情况就是每次+1}// 依次求出 1, 2... 直到 n 的解for(int i = 1; i <= n; i++){// 依次减去一个[完全]平方数for(int j = 1; j * j <= i; j++){dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移方程}}return dp[n];}public static void main(String[] args) {Scanner sc = new Scanner(System.in);while(sc.hasNextInt()){int n = sc.nextInt();int res = numSquares(n);System.out.println(res);}}}
参考:
- 详细通俗的思路分析,多解法
- 完全平方数
- 画解算法:279. 完全平方数
- python3最基础的BFS套路代码,适合入门新手!
- 【超直白】【靠嘴讲】小学生都能看懂的题解,还看不懂我打你~
- 动态规划+BFS 逐行解释 python3
- 不只是答案,而是动态规划类题的思考过程
- Java 解法:将问题转化为图论
附:
递归、记忆化搜索、动态规划之间的联系: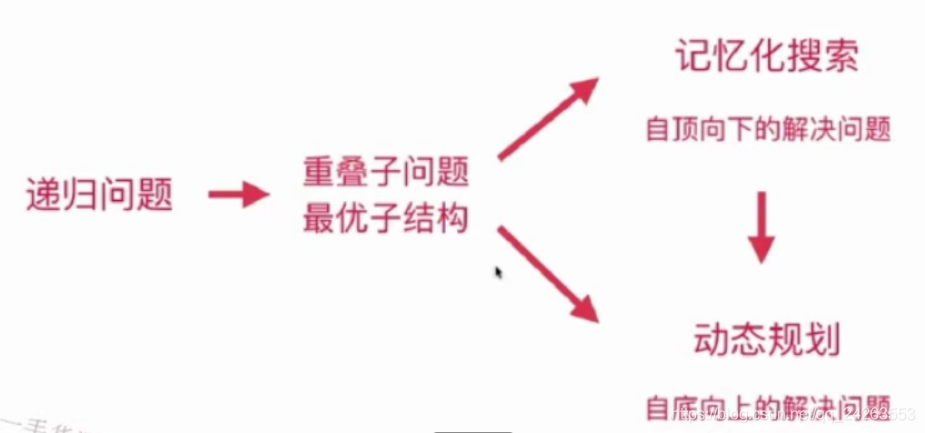





























还没有评论,来说两句吧...