LeetCode - Medium - 39. Combination Sum-蒲公英云

Topic

Array
Backtracking

Description

https://leetcode.com/problems/combination-sum/

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Example 1:

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

Example 4:

Input: candidates = [1], target = 1
Output: [[1]]

Example 5:

Input: candidates = [1], target = 2
Output: [[1,1]]

Constraints:

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
All elements of candidates are distinct.
1 <= target <= 500

Analysis

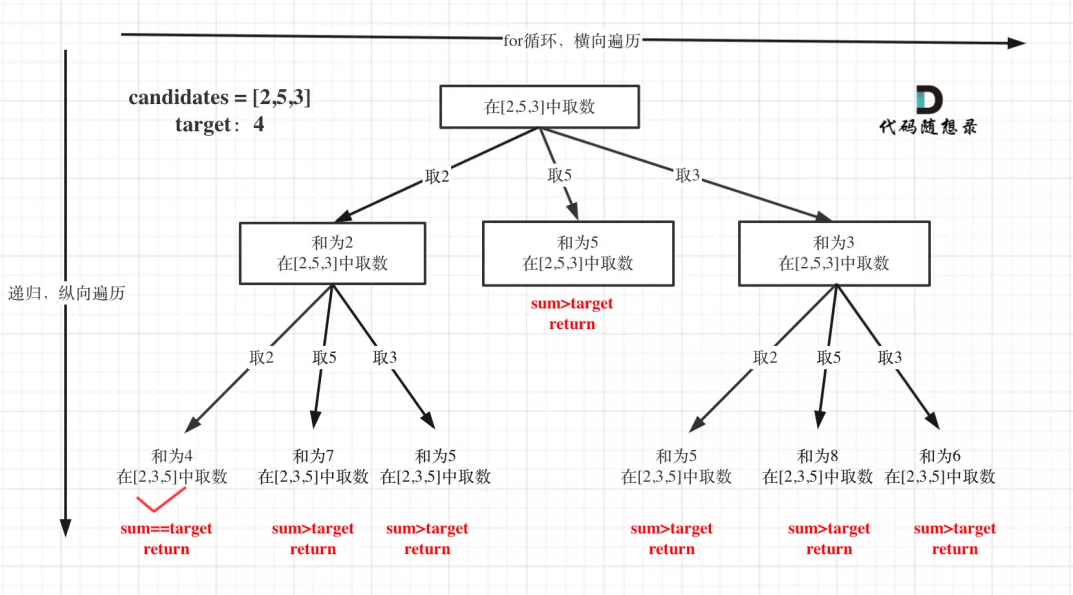
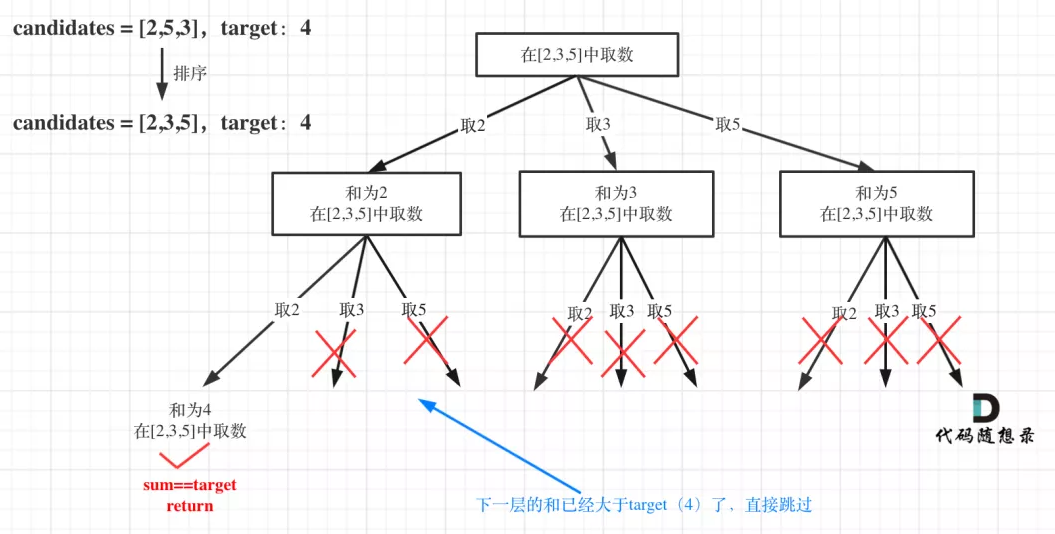
在这里插入图片描述

回溯算法：求组合总和（二）

Submission

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class CombinationSum { 
    public List<List<Integer>> combinationSum1(int[] candidates, int target) { 
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        backtracking1(path, candidates, target, 0, 0, result);
        return result;
    }
    private void backtracking1(List<Integer> path, int[] candidates, //
            int target, int sum, int startIndex, List<List<Integer>> result) { 
        if (sum > target) { 
            return;
        }
        if (sum == target) { 
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) { 
            sum += candidates[i];
            path.add(candidates[i]);
            backtracking1(path, candidates, target, sum, i, result);
            sum -= candidates[i];
            path.remove(path.size() - 1);
        }
    }
    // 剪枝优化后
    public List<List<Integer>> combinationSum2(int[] candidates, int target) { 
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        Arrays.sort(candidates);
        backtracking2(path, candidates, target, 0, 0, result);
        return result;
    }
    private void backtracking2(List<Integer> path, int[] candidates, //
            int target, int sum, int startIndex, List<List<Integer>> result) { 
        if (sum == target) { 
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) { 
            sum += candidates[i];
            path.add(candidates[i]);
            backtracking2(path, candidates, target, sum, i, result);
            sum -= candidates[i];
            path.remove(path.size() - 1);
        }
    }
}

Test

import static org.junit.Assert.*;
import java.util.Arrays;
import org.hamcrest.collection.IsEmptyCollection;
import org.hamcrest.collection.IsIterableContainingInAnyOrder;
import org.junit.Test;
public class CombinationSumTest { 
    @Test
    @SuppressWarnings("unchecked")
    public void test1() { 
        CombinationSum obj = new CombinationSum();
        assertThat(obj.combinationSum1(new int[] {  2, 3, 6, 7 }, 7), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(2, 2, 3), Arrays.asList(7)));
        assertThat(obj.combinationSum1(new int[] {  2, 3, 5 }, 8), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(2, 2, 2, 2), //
                        Arrays.asList(2, 3, 3), Arrays.asList(3, 5)));
        assertThat(obj.combinationSum1(new int[] {  2 }, 1), IsEmptyCollection.empty());
        assertThat(obj.combinationSum1(new int[] {  1 }, 1), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(1)));
        assertThat(obj.combinationSum1(new int[] {  1 }, 2), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(1, 1)));
    }
    @Test
    @SuppressWarnings("unchecked")
    public void test2() { 
        CombinationSum obj = new CombinationSum();
        assertThat(obj.combinationSum2(new int[] {  2, 3, 6, 7 }, 7), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(2, 2, 3), Arrays.asList(7)));
        assertThat(obj.combinationSum2(new int[] {  2, 3, 5 }, 8), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(2, 2, 2, 2), //
                        Arrays.asList(2, 3, 3), Arrays.asList(3, 5)));
        assertThat(obj.combinationSum2(new int[] {  2 }, 1), IsEmptyCollection.empty());
        assertThat(obj.combinationSum2(new int[] {  1 }, 1), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(1)));
        assertThat(obj.combinationSum2(new int[] {  1 }, 2), //
                IsIterableContainingInAnyOrder.containsInAnyOrder(Arrays.asList(1, 1)));
    }
}