ILFO：Adaversarial Attack on Adaptive Neural Networks

不念不忘少年蓝@ 2023-01-13 05:53 63阅读 0赞

## ILFO：Adaversarial Attack on Adaptive Neural Networks ##

`论文收录于CVPR 2020`

### 文章目录 ###

*   *  ILFO：Adaversarial Attack on Adaptive Neural Networks
     *   *  背景
         *  攻击
         *   *   *  攻击形式
                 *   *  Attacking Early-termination AdNN
                     *  Attacking Conditional-skipping AdNN

### 背景 ###

神经网络在一般情况下，模型规模越大，效果越好。但模型跑起来是很耗费资源的，尤其是大型网络，对手持或嵌入式设备很不友好，于是就引发了很多人去研究节约资源的方法。现有的节约资源的方法可以分为两类：

*  On-device Neural Networks(ODNN): 通过低维的filter或更改filter的尺寸来减少计算量
 *  Adaptive Neural Networks(AdNNs): 根据输入动态地停用部分模型来减少计算量 （本文考虑内容）
    
     *  early-termination 代表模型SACT
     *  Conditional-skip 代表模型SkipNet

### 攻击 ###

模型资源的鲁棒性考虑的是输入与其相应的资源消耗之间的关系。

本文的攻击是针对于AdNNs的，通过对图片添加扰动，使生成的图片在AdNNs模型推断的时候，增加计算量，从而使其所用的资源增加，破坏模型的可用性。

AdNNs的工作机制如图所示：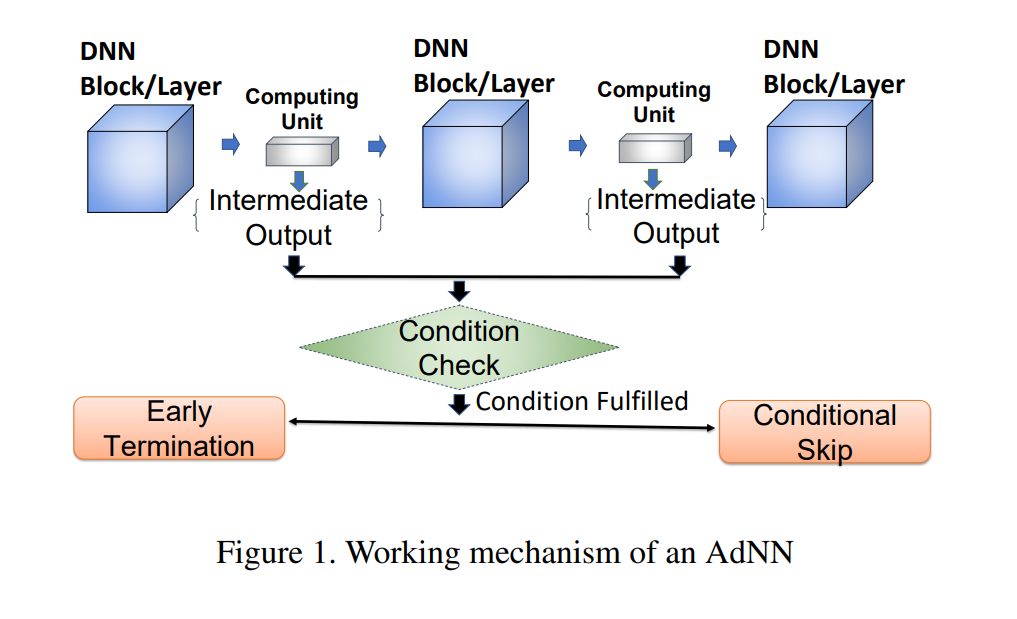  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70]  
在DNN Block或Layer之间有一个小的计算单元，其产生的中间结果决定下一Block或Layer上的操作，有两种操作形式：一种是早停，一种是跳过， 以此来减少计算量。

攻击目标：  
1、被攻击后的样本应该增加推理时的计算量  
2、原样本和对抗样本应该无法区分

定义中间输出的状态：

*  desirable state(des): 在推理时中间输出的最大计算量
 *  current state(cur)： 在推理过程中实际的计算量

优化方法：

minimize( δ \\delta δ \+ c · f(x +  δ \\delta δ)) such that (x +  δ \\delta δ)  ∈ \\in ∈ \[0, 1\]n

其中c是一个正常量，f(·)是损失函数，表示des的cur之间的距离。

##### 攻击形式 #####

###### Attacking Early-termination AdNN ######

使用模型SACT， SACT的工作机制如下图：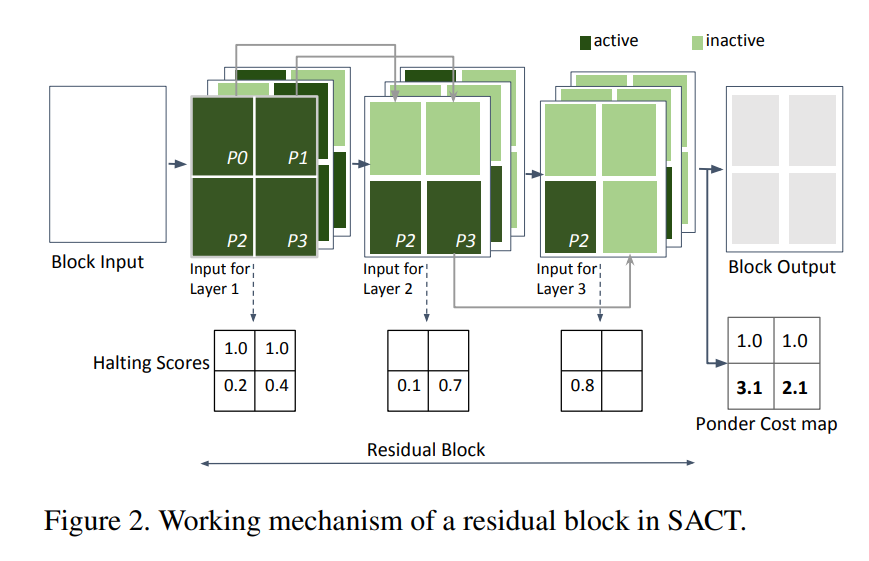  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 1]  
在一个残差块（residual block）中，每一层（layer）都会计算每个位置上的halting score，同一位置上的halting score累加和只有小于1才会激活接下来该位置的计算。为了方便进行攻击，最终每个块都会基于halting score生成Ponder Cost Map。

攻击方式： 通过增加每个位置上的ponder cost来增加每个位置上的计算量。  
攻击过程示例如下图所示：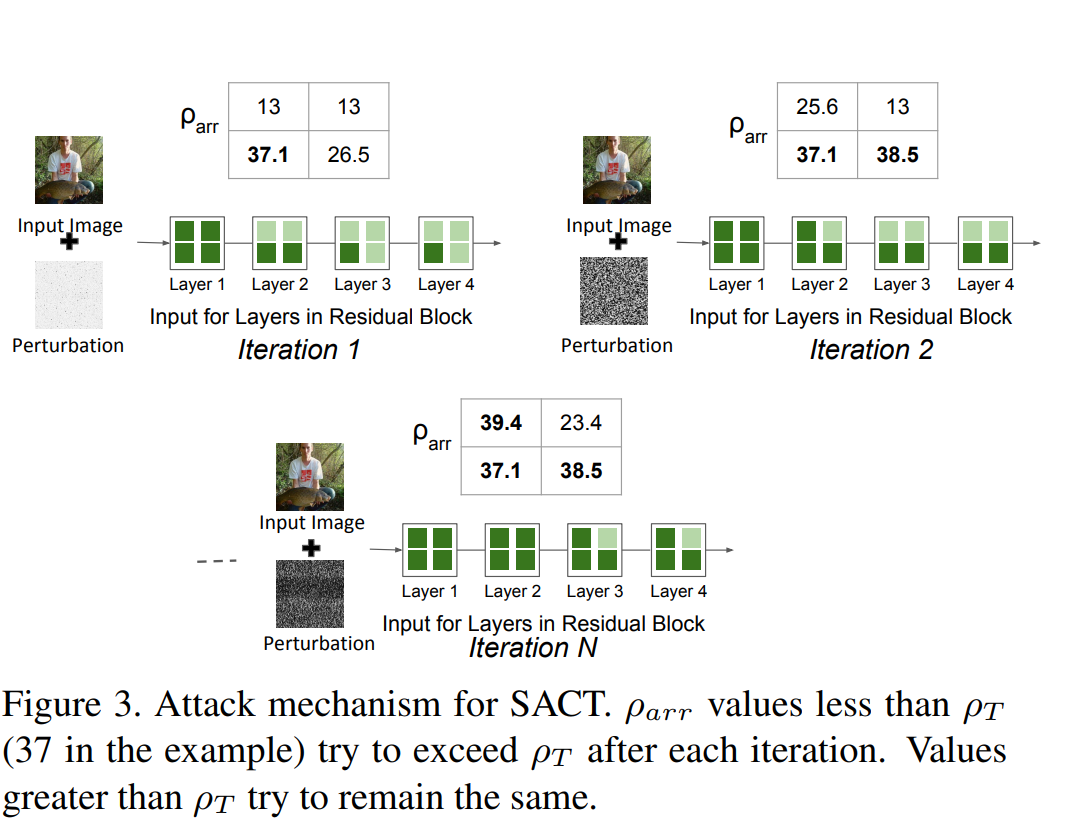  
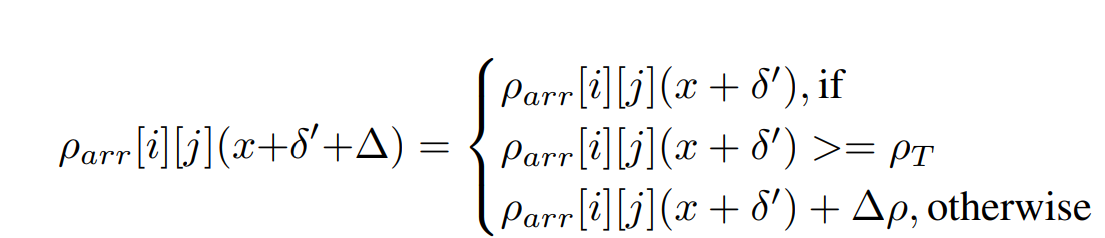
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 2]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 3]

ρ \\rho ρarr代表每块的ponder cost， ρ \\rho ρarr\[i\]\[j\]代表ponder cost第i行第j列上的值， ρ \\rho ρT代表提前定义好的阈值。当 ρ \\rho ρarr\[i\]\[j\]  ≥ \\geq ≥ ρ \\rho ρT的时候， ρ \\rho ρarr\[i\]\[j\]的大小不改变，反之增加 ρ \\rho ρarr\[i\]\[j\]的值。

δ \\delta δ’ 代表累加的扰动，  Δ \\Delta Δ ρ \\rho ρ代表本次迭代添加的扰动。

定义损失函数为：f(x +  δ \\delta δ) =  ∑ i = 0 R \\sum\_\{i=0\}^R ∑i=0R  ∑ j = 0 C \\sum\_\{j=0\}^C ∑j=0C max( ρ \\rho ρmax\[i\]\[j\] \-  ρ \\rho ρarr\[i\]\[j\], 0)  
max(·)保证值不会减小。 ρ \\rho ρmax\[i\]\[j\] =  ρ \\rho ρT

###### Attacking Conditional-skipping AdNN ######

使用模型 SkipNet， SkipNet的工作机制如下图：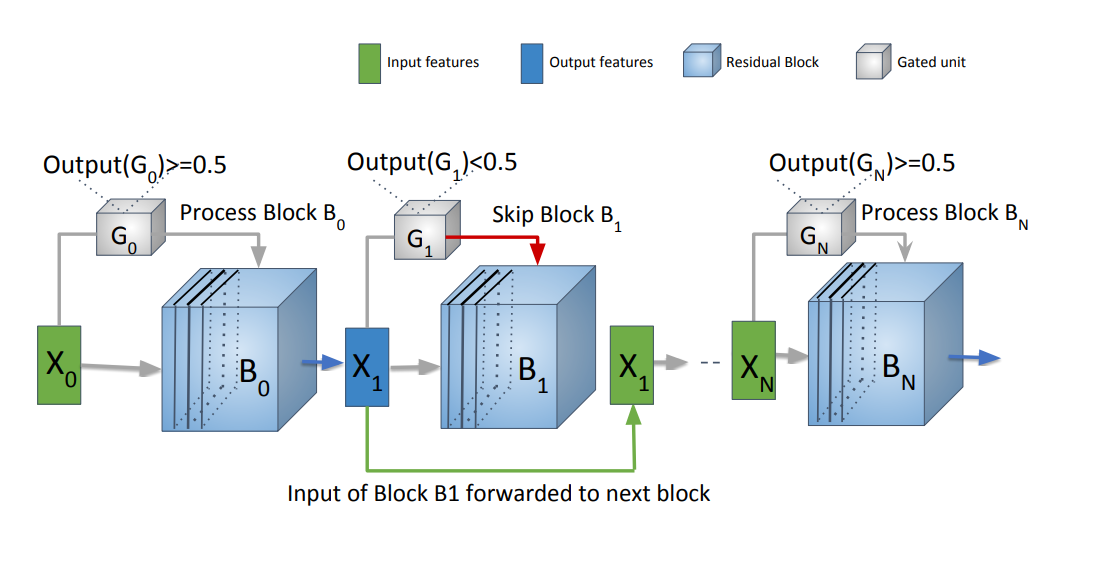  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 4]  
SkipNet模型包含N+1个残差块，每个块有一个对应的Gate。如果Gate的输出Output(G) ≥ \\geq ≥GT（GT是预先设置好的阈值）则下一个块就被激活，否则跳过下一个块。

攻击方式：增加Output（G），激活更多的块来增加计算量  
攻击过程示例如下图所示：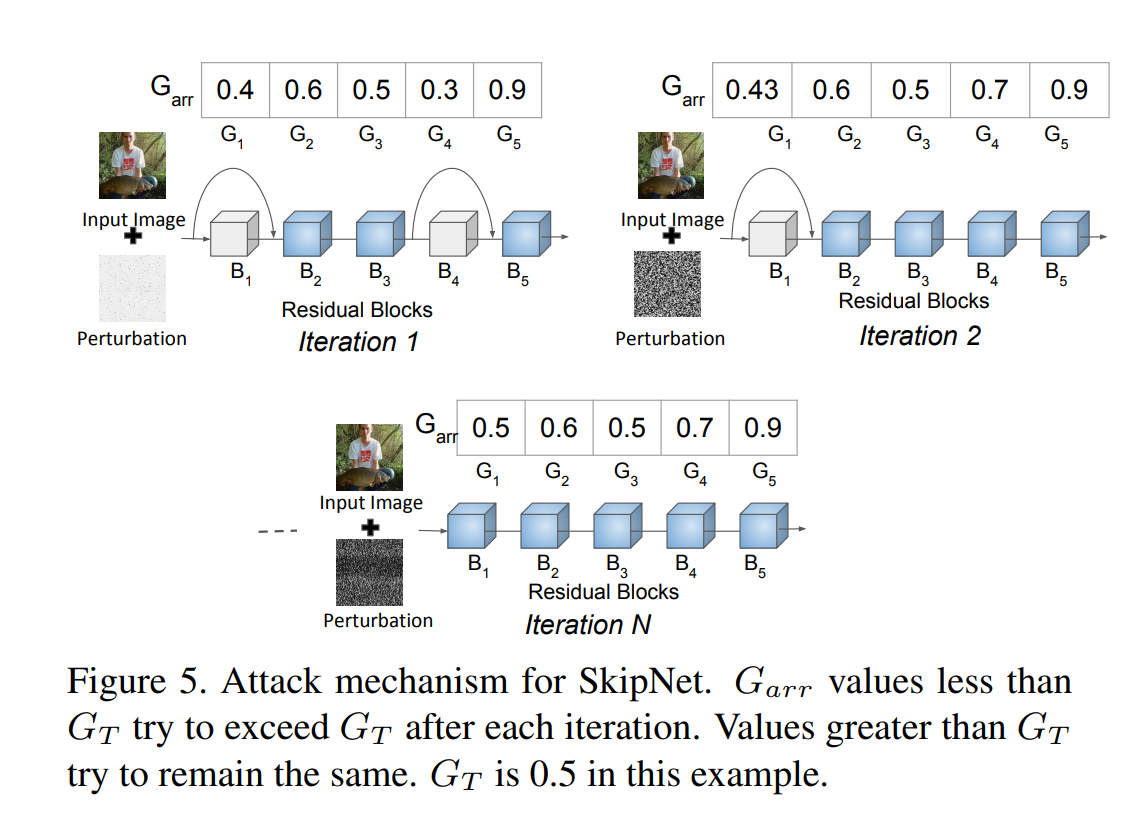  
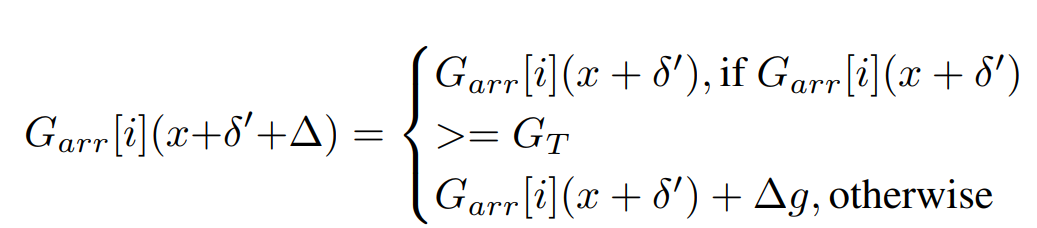
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 5]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 6]  
Garr代表Gate的输出，Garr\[i\]代表第i个gate的输出，GT代表提前设置的阈值。当Garr ≥ \\geq ≥GT的时候保持不变，否则增加Garr的值。

δ \\delta δ’ 代表累加的扰动，  Δ \\Delta Δ g g g代表本次迭代添加的扰动。

定于损失函数为：f(x +  δ \\delta δ) =  ∑ i = 0 N \\sum\_\{i=0\}^N ∑i=0N max(Gmax\[i\] \- Garr\[i\], 0)  
max(·)保证值不会减小。Gmax\[i\] = GT

[code][]  
[paper][]

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70]: /images/20221022/a135d29c9562406e81ba69c5a7bdaca8.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 1]: /images/20221022/6b49a59cb8ba4307bbb2bfff453ee6a9.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 2]: /images/20221022/b99f1de29386416e9b40d59c16dfa668.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 3]: /images/20221022/71e1d3b31a394d538e47090ae104032b.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 4]: /images/20221022/3acaf8bf60b944a49775af3df4a0341a.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 5]: /images/20221022/8bf756c6826846399e4e24876519088c.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NpbmF0XzM2MDU5NjUz_size_16_color_FFFFFF_t_70 6]: /images/20221022/ced96b32d45e4e67a4fa07f941dd4b2c.png
[code]: https://github.com/anonymous2015258/ILFO-Adversarial-Attack-on-AdNN
[paper]: http://youngwei.com/pdf/ILFO.pdf